Table of Contents
In Chapter 3 we have introduced the architecture of the XT tansformation tools. Source to source transformation systems based on XT consist of a pipeline of a parser, a series of transformations on a structured program representation, and a pretty-printer. In Chapter 4 we have explained the ATerm format, which is the format we use for this structured program transformation. This chapter will be about the parser part of the pipeline.
Stratego/XT uses the Syntax Definition Formalism (SDF), for defining the syntax of a programming language. From a syntax definition in SDF, a parser can be generated fully automatically. There is no need for a separate lexer or scanner specification, since SDF integrates the lexical and the context-free syntax definition of a programming language in a single specification. The generated parser is based on the Scannerless Generalized-LR algorithm, but more details about that later. The parser directly produces an ATerm representation of the program, as a parse tree, or as an abstract syntax tree.
Actually, the component-based approach of XT allows you to use any tool for parsing a source program to an ATerm. So, you don't necessarily have to use the parsing tools we present in this chapter. Instead, it might sometimes be a good idea to create an ATerm backend for a parser that you already have developed (by hand or using a different parser generator), or reuse an entire, existing front-end that is provided by a third-party. However, the techniques we present in this chapter are extremely expressive, flexible, and easy to use, so for developing a new parser it would be a very good idea to use SDF and SGLR.
In this section, we review the basics of grammars, parse trees and abstract syntax trees. Although you might already be familiar with these basic concepts, the perspective from the Stratego/XT point of view might still be interesting to read.
Context-free grammars were originally introduced by Chomsky to describe the generation of grammatically correct sentences in a language. A context-free grammar is a set of productions of the form A0 -> A1 ... An, where A0 is non-terminal and A1 ... An is a string of terminals and non-terminals. From this point of view, a grammar describes a language by generating its sentences. A string is generated by starting with the start non-terminal and repeatedly replacing non-terminal symbols according to the productions until a string of terminal symbols is reached.
A context-free grammar can also be used to recognize sentences in the language. In that process, a string of terminal symbols is rewritten to the start non-terminal, by repeatedly applying grammar productions backwards, i.e. reducing a substring matching the right-hand side of a production to the non-terminal on the left-hand side. To emphasize the recognition aspect of grammars, productions are specified as A1 ... An -> A0 in SDF.
As an example, consider the SDF productions for a small language
of arithmetic expressions in Figure 5.1, where Id
and IntConst are terminals and Var and
Exp are non-terminals. Using this definition, and
provided that a and n are identifiers
(Id) and 1 is an
IntConst, a string such as (a+n)*1 can
be recognized as an expression by reducing it to
Exp, as shown by the reduction sequence in the
right-hand side of Figure 5.1.
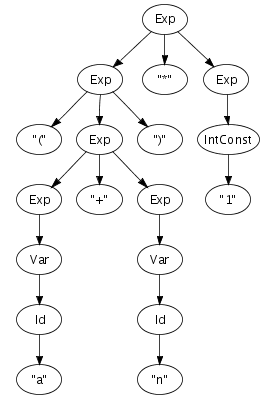
Figure 5.1. Context-free productions and a reduction sequence.
Id -> Var
Var -> Exp
IntConst -> Exp
"-" Exp -> Exp
Exp "*" Exp -> Exp
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
"(" Exp ")" -> Exp
|
(a + n ) * 1 -> (Id + n ) * 1 -> (Var + n ) * 1 -> (Exp + n ) * 1 -> (Exp + Id ) * 1 -> (Exp + Var) * 1 -> (Exp + Exp) * 1 -> (Exp ) * 1 -> Exp * 1 -> Exp * IntConst -> Exp * Exp -> Exp |
Recognition of a string only leads to its grammatical category, not to any other information. However, a context-free grammar not only describes a mapping from strings to sorts, but actually assigns structure to strings. A context-free grammar can be considered as a declaration of a set of trees of one level deep. For example, the following trees correspond to productions from the syntax definition in Figure 5.1:
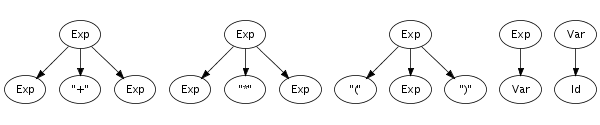
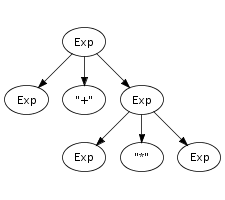
Such one-level trees can be composed into larger trees by fusing
trees such that the symbol at a leaf of one tree matches with
the root symbol of another, as is illustrated in the fusion of
the plus and times productions on the right.
The fusion process can continue as long as the tree has
non-terminal leaves. A tree composed in this fashion is a parse
tree if all leaves are terminal symbols. Figure 5.2 shows a parse tree for the expression
(a+n)*1, for which we showed a reduction sequence
earlier in Figure 5.1. This
illustrates the direct correspondence between a string and its
grammatical structure. The string underlying a parse tree can be
obtained by concatening the symbols at its leaves, also known as
the yield.
Parse trees can be derived from the reduction sequence induced by the productions of a grammar. Each rewrite step is associated with a production, and thus with a tree fragment. Instead of replacing a symbol with the non-terminal symbol of the production, it is replaced with the tree fragment for the production fused with the trees representing the symbols being reduced. Thus, each node of a parse tree corresponds to a rewrite step in the reduction of its underlying string. This is illustrated by comparing the reduction sequence in Figure 5.1 with the tree in Figure 5.2
The recognition of strings described by a syntax definition, and the corresponding construction of parse trees can be done automatically by a parser, which can be generated from the productions of a syntax definition.
Parse trees contain all the details of a program including
literals, whitespace, and comments. This is usually not
necessary for performing transformations. A parse tree is
reduced to an abstract syntax tree by
eliminating irrelevant information such as literal symbols and
layout. Furthermore, instead of using sort names as node labels,
constructors encode the production from
which a node is derived. For this purpose, the productions in a
syntax definition are extended with constructor
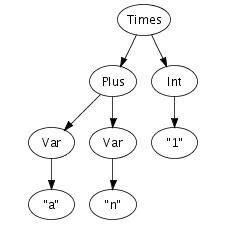
annotations. Figure 5.3 shows
the extension of the syntax definition from Figure 5.1 with constructor
annotations and the abstract syntax tree for the same good old
string (a+n)*1. Note that some identifiers are used
as sort names and and as constructors. This
does not lead to a conflict since sort names and constructors
are derived from separate name spaces. Some productions do not
have a constructor annotation, which means that these
productions do not create a node in the abstract syntax tree.
Figure 5.3. Context-free productions with constructor annotations and an abstract syntax tree.
Id -> Var {cons("Var")}
Var -> Exp
IntConst -> Exp {cons("Int")}
"-" Exp -> Exp {cons("Uminus")}
Exp "*" Exp -> Exp {cons("Times")}
Exp "+" Exp -> Exp {cons("Plus")}
Exp "-" Exp -> Exp {cons("Minus")}
Exp "=" Exp -> Exp {cons("Eq")}
Exp ">" Exp -> Exp {cons("Gt")}
"(" Exp ")" -> Exp
|  |
In the next section we will take a closer look at the various features of the SDF language, but before that it is useful to know your tools, so that you can immediately experiment with the various SDF features you will learn about. You don't need to fully understand the SDF fragments we use to explain the tools: we will come back to that later.
One of the nice things about SDF and the tools for it, is that the concepts that we have discussed directly translate to practice. For example, SDF supports all context-free grammars; the parser produces complete parse trees, which can even be yielded; parse trees can be converted to abstract syntax trees.
In SDF, you can split a syntax definition into multiple
modules. So, a complete syntax definition consists of a set
modules. SDF modules are stored in files with the extension
.sdf. Figure 5.4 shows
two SDF modules for a small language of expressions. The module
Lexical defines the identifiers and integer
literals of the language. This module is imported by the module
Expression.
Figure 5.4. SDF modules for a small language of arithmetic expressions.
module Expression
imports
Lexical Operators
exports
context-free start-symbols Exp
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")}
"(" Exp ")" -> Exp {bracket}
|
module Operators
exports
sorts Exp
context-free syntax
Exp "*" Exp -> Exp {left, cons("Times")}
Exp "/" Exp -> Exp {left, cons("Div")}
Exp "%" Exp -> Exp {left, cons("Mod")}
Exp "+" Exp -> Exp {left, cons("Plus")}
Exp "-" Exp -> Exp {left, cons("Minus")}
context-free priorities
{left:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
|
module Lexical
exports
sorts Id IntConst
lexical syntax
[\ \t\n] -> LAYOUT
[a-zA-Z]+ -> Id
[0-9]+ -> IntConst
|
Before you can invoke the parser generator to create a parser
for this expression language, the modules that constitute a
complete syntax definition have to be collected into a single
file, usually called a definition. This
file has the extension .def. Collecting SDF
modules into a .def file is the job of the
tool pack-sdf.
$ pack-sdf -i Expression.sdf -o Expression.def
Pack-sdf collects all modules imported by the SDF module
specified using the -i parameter. This results in a
combined syntax definition, which is written to the file
specified with the -o parameter. Modules are looked
for in the current directory and any of the include directories
indicated with the -I dir arguments.
Pack-sdf does not analyse the contents of an SDF module to report possible errors (except for syntactical ones). The parser generator, discussed next, performs this analysis.
Standard options for input and output
All tools in Stratego/XT use the -i and
-o options for input and output. Also, most tools
read from the standard input or write to standard output if no
input or output is specified.
From the .def definition file (as produced by
pack-sdf), the parser
generator sdf2table constructs
a parse table. This parse table can later on be handed off to
the actual parser.
$ sdf2table -i Expression.def -o Expression.tbl -m Expression
The -m option is used to specify the module for
which to generate a parse table. The default module is
Main, so if the syntax definition has a different
main module (in this case Expression), then you
need to specify this option.
The parse table is stored in a file with extension
.tbl. If all you plan on doing with your grammar is
parsing, the resulting .tbl file is all you need to
deploy. sdf2table could be thought of as a
parse-generator; however, unlike many other parsing systems, it
does not construct an parser program, but a compact data
representation of the parse table.
Sdf2table analyzes the SDF syntax definition to detect possible
errors, such as undefined symbols, symbols for which no
productions exists, deprecated features, etc. It is a good idea
to try to fix these problems, although sdf2table
will usually still happily generated a parse table for you.
Now we have a parse table, we can invoke the actual parser with
this parse table to parse a source program. The parser is called
sglr and produces a
complete parse tree in the so-called AsFix
format. Usually, we are not really interested in the parse tree
and want to work on an abstract syntax tree. For this, there is
the somewhat easier to use tool sglri,
which indirectly just invokes sglr.
$cat mul.exp (a + n) * 1$sglri -p Expression.tbl -i mul.exp Times(Plus(Var("a"),Var("n")),Int("1"))
For small experiments, it is useful that sglri can also read the source file from standard input. Example:
$ echo "(a + n) * 1" | sglri -p Expression.tbl
Times(Plus(Var("a"),Var("n")),Int("1"))
Heuristic Filters. As we will discuss later, SGLR uses disambiguation filters to select the desired derivations if there are multiple possibilities. Most of these filters are based on specifications in the original syntax definition, such a associativity, priorities, follow restrictions, reject, avoid and prefer productions. However, unfortunately there are some filters that select based on heuristics. Sometimes these heuristics are applicable to your situation, but sometimes they are not. Also, the heuristic filters make it less clear when and why there are ambiguities in a syntax definition. For this reason, they are disabled by default if you use sglri, (but not yet if you use sglr).
Start Symbols.
If the original syntax definition contained multiple start
symbols, then you can optionally specify the desired start
symbol with the -s option. For example, if we add
Id to the start-symbols of our
expression language, then a single identifier is suddenly an
ambiguous input (we will come back to ambiguities later) :
$ echo "a" | sglri -p Expression.tbl
amb([Var("a"),"a"])
By specifying a start symbol, we can instruct the parser to give us the expression alternative, which is the first term in the list of two alternatives.
$ echo "a" | sglri -p Expression.tbl -s Exp
Var("a")Working with Parse Trees. If you need a parse tree, then you can use sglr itself. These parse trees contain a lot of information, so they are huge. Usually, you really don't want to see them. Still, the structure of the parse tree is quite interesting, since you can exactly inspect how the productions from the syntax definition have been applied to the input.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | pp-aterm
parsetree( ... )
Note that we passed the options -2 -fi -fe to
sglr. The -2 option specifies the
variant of the AsFix parse tree format that should be used:
AsFix2. The Stratego/XT tools use this variant at the
moment. All variants of the AsFix format are complete and
faithful representation of the derivation constructed by the
parser. It includes all details of the input file, including
whitespace, comments, and is self documenting as it uses the
complete productions of the syntax definition to encode node
labels. The AsFix2 variant preserves all the structure of the
derivation. In the other variant, the structure of the lexical
parts of a parse tree are not preserved. The -fi
-fe options are used to heuristic disambiguation filters,
which are by default disabled in sglri, but not in
sglr.
The parse tree can be imploded to an abstract syntax tree
using the tool implode-asfix. The
combination of sglr and
implode-asfix has the same effect as directly
invoking sglri.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | implode-asfix
Times(Plus(Var("a"),Var("n")),Int("1"))The parse tree can also be yielded back to the original source file using the tool asfix-yield. Applying this tool shows that whitespace and comments are indeed present in the parse tree, since the source is reproduced in exactly the same way as it was!
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | asfix-yield
(a + n) * 1