Table of Contents
The Annotated Term Format, or ATerms for short, is heavily used in Stratego/XT. It used for the structured representation of programs (and also data in general). Program representations are exchanged between transformation tools in the ATerm format and the data-structures of the Stratego language itself are ATerms.
Before we start with the more interesting tools of XT, we need to take a closer look at the ATerm format. This chapter introduces the ATerm format and some tools that operate on ATerms.
The ATerm format provides a set of constructs for representing
trees, comparable to XML or abstract data types in functional
programming languages. For example, the code 4 + f(5 *
x) might be represented in a term as:
Plus(Int("4"), Call("f", [Mul(Int("5"), Var("x"))]))ATerms are constructed from the following elements:
- Integer
-
An integer constant, that is a list of decimal digits, is an ATerm. Examples:
1,12343. - String
-
A string constant, that is a list of characters between double quotes is an ATerm. Special characters such as double quotes and newlines should be escaped using a backslash. The backslash character itself should be escaped as well.
Examples:
"foobar","string with quotes\"","escaped escape character\\ and a newline\n". - Constructor application
-
A constructor is an identifier, that is an alphanumeric string starting with a letter, or a double quoted string.
A constructor application
c(t1,...,tn)creates a term by applying a constructor to a list of zero or more terms. For example, the termPlus(Int("4"),Var("x"))uses the constructorsPlus,Int, andVarto create a nested term from the strings"4"and"x".When a constructor application has no subterms the parentheses may be omitted. Thus, the term
Zerois equivalent toZero(). Some people consider it good style to explicitly write the parentheses for nullary terms in Stratego programs. Through this rule, it is clear that a string is really a special case of a constructor application. - List
-
A list is a term of the form
[t1,...,tn], that is a list of zero or more terms between square brackets.While all applications of a specific constructor typically have the same number of subterms, lists can have a variable number of subterms. The elements of a list are typically of the same type, while the subterms of a constructor application can vary in type.
Example: The second argument of the call to
"f"in the termCall("f",[Int("5"),Var("x")])is a list of expressions. - Tuple
-
A tuple
(t1,...,tn)is a constructor application without constructor. Example:(Var("x"), Type("int")) - Annotation
-
The elements defined above are used to create the structural part of terms. Optionally, a term can be annotated with a list terms. These annotations typically carry additional semantic information about the term. An annotated term has the form
t{t1,...,tn}. Example:Lt(Var("n"),Int("1")){Type("bool")}. The contents of annotations is up to the application.
As a Stratego programmer you will be looking a lot at raw ATerms. Stratego pioneers would do this by opening an ATerm file in emacs and trying to get a sense of the structure by parenthesis highlighting and inserting newlines here and there. These days your life is much more pleasant through the tool pp-aterm, which adds layout to a term to make it readable. For example, parsing the following program
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n - 1))
in printint(fact(10))
end
produces the following ATerm (say in file fac.trm):
Let([FunDecs([FunDec("fact",[FArg("n",Tp(Tid("int")))],Tp(Tid("int")),
If(Lt(Var("n"),Int("1")),Int("1"),Seq([Times(Var("n"),Call(Var("fact"),
[Minus(Var("n"),Int("1"))]))])))])],[Call(Var("printint"),[Call(Var(
"fact"),[Int("10")])])])
By pretty-printing the term using pp-aterm as
$ pp-aterm -i fac.trm
we get a much more readable term:
Let(
[ FunDecs(
[ FunDec(
"fact"
, [FArg("n", Tp(Tid("int")))]
, Tp(Tid("int"))
, If(
Lt(Var("n"), Int("1"))
, Int("1")
, Seq(
[ Times(
Var("n")
, Call(
Var("fact")
, [Minus(Var("n"), Int("1"))]
)
)
]
)
)
)
]
)
]
, [ Call(
Var("printint")
, [Call(Var("fact"), [Int("10")])]
)
]
)
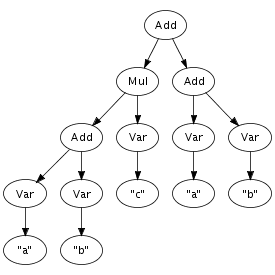
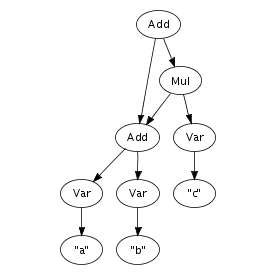
An important feature of the implementation is that terms are represented using maximal sharing. This means that any term in use in a program is represented only once. In other words, two occurrences of the same term will be represented by pointers to the same location. Figure 4.1 illustrates the difference between a pure tree representation and a tree, or more accurately, a directed acyclic graph, with maximal sharing. That is, any sub-term is represented exactly once in memory, with each occurrence pointing to the same memory location. This representation entails that term equality is a constant operation, since it consists of comparing pointers.
It should be noted that annotations create different terms, that is, two terms, one with and the other without annotations that are otherwise, modulo annotations, the same, are not equal.
Maximal sharing can make a big difference in the amount of bytes needed for representing programs. Therefore, we would like to preserve this maximal sharing when an ATerm is exchanged between two programs. When exporting a term using the textual exchange format, this compression is lost. Therefore, the ATerm Library also provides a binary exchange format that preserves maximal sharing.
Actually, there are three different formats:
- Textual ATerm Format
-
In the textual ATerm format the ATerm is written as plain text, without sharing. This format is very inefficient for the exchange of large programs, but it is readable for humans.
- Binary ATerm Format
-
The binary ATerm format, also known as BAF, is an extremely efficient binary encoding of an ATerm. It preserves maximal sharing and uses all kinds of tricks to represent an ATerm in as few bytes as possible.
- Shared Textual ATerm Format
-
In the shared, textual, format the ATerm is written as plain text, but maximal sharing is encoded in the text.
The tool baffle can be used to convert an ATerm from one format to another. Baffle, and other tools that operate on ATerms, automatically detect the format of an input ATerm.
The ATerm Format is an external representation for terms that can be used to exchange structured data between programs. In order to use a term, a program needs to parse ATerms and transform them into some internal representation. To export a term after processing it, a program should transform the internal representation into the standard format. There are libraries supporting these operation for a number of languages, including C, Java, and Haskell.
The implementation of the Stratego transformation language is based on the C implementation of the library. The library provides term input and output, and an API for constructing and inspecting terms. Garbage collection is based on Boehms conservative garbage collection algorithm.