Table of Contents
- I. Introduction
- II. The XT Transformation Tools
- III. The Stratego Language
- IV. The Stratego Library
List of Figures
- 1.1. Applications of Software Transformation.
- 1.2. Pipeline of a software transformation system.
- 1.3. file: sample-rules.str
- 3.1. Pipeline of a software transformation system.
- 3.2. Syntax definitions play a central role in a transformation system.
- 4.1.
Tree and dag for the string
(a + b) * c + (a + b) - 5.1. Context-free productions and a reduction sequence.
- 5.2. Parse tree
- 5.3. Context-free productions with constructor annotations and an abstract syntax tree.
- 5.4. SDF modules for a small language of arithmetic expressions.
- 6.1. Syntax definition with regular expressions.
- 8.1. Signature for statement and expression constructors, automatically derived from a syntax definition.
- 9.1. Unparsing an abstract syntax tree.
- 9.2. Unparsing table
- 9.3. Pretty-printing with Box markup
- 9.4. Pretty-print table with Box markup
- 9.5. Pretty-printing of if-then-else statement
List of Examples
Table of Contents
Imagine finding yourself in a situation where you have a collection of files containing source code. If this is an unreasonable prospect for you, stop reading and pick another tutorial. If you are still with us, consider these files the blueprints for your software. They are still not the award-winning, executable program you are aiming for, but by applying a compiler to them, you can generate one (with some minor provisions about syntactial and semantical correctness). If so inclined, you may also run a documentation generator like Javadoc on the source, to generate structured documentation. Or, while colleagues are not looking, you can secretly invoke tools like lint (C/C++) or FindBugs (Java) to weed out common programming errors.
The compilation, documentation generation and source-code analysis are all examples of software transformations , but they are certainly not the only ones. Software transformation has been used by the mathematically inclined for generating programs from high-level specifications, by forgetful people to recover lost design and architecture from legacy code and by reverse-engineers to obtain high-level, readable code from binary files after somebody accidentally misplaced a stack of backup tapes. Specialization of a program to known inputs in order to improve performance, optimization using domain knowledge from the application domain and improving program understanding by analysing sources are also favoured topics among software transformers.
But who uses software transformation, anyway? People with a problem resembling any in Figure 1.1 are. Compilation, the translation of a program to machine code in order to make it executable, is the standard processing technique applied to get running programs out of source code. But much more can be done. There are many other kinds of processes that can be applied to programs. For example, programs can be synthesized from high-level specifications; programs can be optimized using knowledge of the application domain; documentation for understanding a program can be automatically derived from its sources; programs can be specialized to known inputs; application programs can be generated from domain-specific languages; low-level programs can be reverse engineered into high-level programs.
All too often, Real Programmers facing such problems are of the opinion that software transformation is overly complicated dark magic, and that simple regular expression hacks solve the problem just fine. Almost equally often, their ad-hoc, text-based solutions turn out to be brittle, overly complicated and acquire a status of dark magic, with the result that no other team member dears touch the stuff. Most of the time, the problem would be easily solved in a maintainable and robust way if only the right tool could be found.
Figure 1.1. Applications of Software Transformation.
Compilers
-
Translation, e.g. Stratego into C
Desugaring, e.g. Java's
foreachintoforInstruction selection
-
Maximal munch
BURG-style dynamic programming
Optimization
-
Data-flow optimization
Vectorization
GHC-style simplification
Deforestation
Domain-specific optimization
Partial evaluation
Type checking
Specialization of dynamic typing
Program generators
-
Pretty-printer and signature generation from syntax definitions
Application generation, e.g. data format checkers from specifications
Program migration
-
Grammar conversion, e.g. YACC to SDF
Program understanding
-
Documentation generation, e.g. API documentation for Stratego
Document generation/transformation
-
Web/XML programming (server-side scripts)
So what do should you do if you have a mountain of source code that you have to do some transformation on? Obviously, using the the right tool for the job is a good start. We don't recommend using toothpicks to move software mountains. Instead, we think using Stratego for this is a good idea. In this tutorial, we will use small, understandable and cute examples that you can try out in the leisure of your own desktop. We hope these will convince you exactly how good an idea using Stratego for software transformation really is.
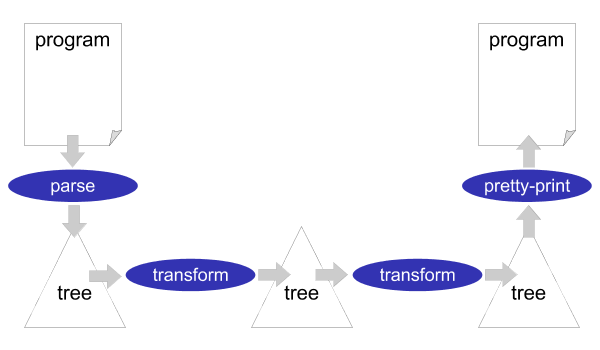
Stratego/XT is a framework for implementing software transformation systems. A software transformation system is usually organized as a simple pipeline of transformation steps, see Figure 1.2. At the source of the pipeline (far left), a parser reads the text of the input program and turns it into a parse tree or abstract syntax tree. Subsequently, one or several transformations components modify the tree. At the sink of the pipeline (far right), a pretty-printer turns the output tree into program text. The output program need not be in the same language as the input program. It need not even be a programming language. This allows us to create important tools such as compilers and documentation generators using Stratego/XT.
The Stratego/XT framework consists of two parts: Stratego, a language for implementing software transformations, and XT, a collection of transformation tools. The Stratego language is a powerful language for implementing the core transformations of a complete transformation system. The XT tools help with the implementation of the infrastructure required around these core transformations, such as a parser and a pretty-printer.
Stratego and XT aim at better productivity in the development of transformation systems through the use of a high-level representations of programs, domain-specific languages for the development of parts of a transformation system, and generating various aspects of a transformation system automatically.
The main ingredients of Stratego/XT are:
- ATerm Format
-
Although some transformation systems work directly on text, in general a textual representation is not adequate for performing complex transformations. Therefore, a structured representation is used by most systems. Since programs are written as texts by programmers, parsers are needed to convert from text to structure and unparsers are needed to convert structure to text.
The basic assumptions in our approach are that programs can be represented as trees, or terms, and that term rewrite rules are an excellent way to formalize transformations on programs. Stratego/XT uses the Annotated Term Format, or ATerms for short, as term representation. The Stratego run-time system is based on the ATerm Library which provides support for internal term representation as well as their persistent representation in files. This makes it easy to provide input and output for terms in Stratego, and to exchange terms between transformation tools.
- Stratego Language
-
Stratego is the core of Stratego/XT. It is a language for software transformation based on the paradigm of rewriting strategies. Basic transformations are defined using conditional term rewrite rules. These are combined into full fledged transformations by means of strategies, which control the application of rules.
Term rewrite systems are formalisations of systematic modifications of terms or trees. A rewrite rule describes how a program fragment matching a certain pattern is transformed into another program fragment. Term rewriting is the exhaustive application of a set of rules to a term.
A complex software transformation is achieved through a number of consecutive modifications of a program. At least at the level of design it is useful to distinguish transformation rules from transformation strategies. A rule defines a basic step in the transformation of a program. A strategy is a plan for achieving a complex transformation using a set of rules.
Figure 1.3. file: sample-rules.str
rules InlineF : |[ let f(xs) = e in e'[f(es)] ]| -> |[ let f(xs) = e in e'[e[es/xs]] ]| InlineV : |[ let x = e in e'[x] ]| -> |[ let x = e in e'[e] ]| Dead : |[ let x = e in e' ]| -> |[ e' ]| where <not(in)> (x,e') Extract(f,xs) : |[ e ]| -> |[ let f(xs) = e in f(xs) ]| Hoist : |[ let x = e1 in let f(xs) = e2 in e3 ]| -> |[ let f(xs) = e2 in let x = e1 in e3 ]| where <not(in)> (x, <free-vars> e2)
For example, consider the transformation rules above. TheInline*rules define inlining of function and variable definitions. TheDeadrule eliminates an unused variable definition. TheExtractrule abstracts an expression into a function. TheHoistrule defines lifting a function definition out of a variable definition if the variable is not used in the function. Using this set of rules, different transformations can be achieved. For example, a constant propagation strategy in an optimizer could use theInlineVandDeadrules to eliminate constant variable definitions:let x = 3 in x + y -> let x = 3 in 3 + y -> 3 + y
On the other hand, the
ExtractFunctionstrategy in a refactoring browser could use theExtractandHoistrules to abstract addition withyinto a new function and lift it to top-level.let x = 3 in x + y -> let x = 3 in let addy(z) = z + y in addy(x) -> let addy(z) = z + y in let x = 3 in addy(x)
Conceptually, rules could be applied interactively by a programmer via a graphical user interface. In Stratego/XT, you can use the Stratego Shell for doing this. More on this later. The problem with such interative manipulations is that the transformation is not reproducible, since the decisions have not been recorded. We want to be able to automate the transformation process, because we can then apply series of basic transformations repeatedly to a program. By generalizing the sequence of transformations, the combined transformation can be applied to many programs. This requires a mechanism for combining rules into more complex transformations, and this is exactly what the Stratego language gives us.
Pure term rewriting is not adequate for the implementation of software transformation systems, since most rewrite systems are non-confluent and/or non-terminating. Hence, standard rewriting strategies are not applicable. The paradigm of programmable rewriting strategies solves this problem by supporting the definition of strategies adapted to a specific transformation system. This makes it possible to select which rule to apply in which transformation stage, and using which traversal order.
- SDF Language
-
Converting program texts to terms for transformations requires parsers. Since Stratego programs operate on terms, they do not particularly care about the implementation of parsers. Thus, parsers can be implemented with any parsing technology, or terms can be produced by an existing compiler front-end. In practice, Stratego is mostly used together with the syntax definition formalism SDF. The Stratego compiler itself uses SDF to parse Stratego programs, and many Stratego applications have been developed with SDF as well.
The syntax definition formalism SDF supports high-level, declarative, and modular definition of the syntax of programming languages and data formats. The formalism integrates the definition of lexical and context-free syntax. The modularity of the formalism implies that it is possible to easily combine two languages or to embed one language into another.
- GPP and the Box Language
-
Stratego/XT uses the pretty-printing model provided by the Generic Pretty-Printing package GPP. In this model a tree is unparsed to a Box expression, which contains text with markup for pretty-printing. A Box expression can be interpreted by different back-ends to produce formatted output for different displaying devices such as plain text, HTML, and LATEX.
- XT tool collection
-
XT is a collection of transformation tools providing support for the generation of many infrastructural aspects of program transformation systems, including parsers, pretty-printers, parenthesizers, and format checkers.
- XTC
-
Parsers, pretty-printers, and transformations can be encapsulated in separate executable components, which can be reused in multiple transformation systems. Composition of such components is facilitated by the XTC transformation tool composition library. Initially this tutorial uses separate components that are glued using shell scripts, in order to improve the understanding of the separate components. The use of XTC is introduced later on.
Exactly what all this means will become clear to you as we move along in this tutorial.
This tutorial is divided into three parts. The first part introduces the XT architecture and many of the tools from the XT collection. An important point in this part that is how to construct parsers using the syntax definition formalism SDF. The parser takes source code text into structured ATerms. Another point in this part is the reverse action: going from ATerms back to source code text.
The second part of the tutorial introduces the Stratego language, starting with the concept of terms and moving on to rules and strategies. After explaining how rules and strategies may be combined to create complete transformation programs, the more advanced topics of concrete syntax and dynamic rules are covered.
The third and final part of the tutorial explains the most important strategies found in the Stratego library: basic data types such as lists, strings, hashtables and sets; basic I/O functionality; the SUnit framework for unit testing. This part also explains the technical details of how to put together complete software transformation systems from XT components using the Stratego build system, using the XTC component composition model.
Table of Contents
The Stratego/XT project distributes several packages. So let's first make clear what you actually need to install. Stratego/XT itself is a language independent toolset for constructing program transformation systems. Language-specific extensions of Stratego/XT are distributed as separate packages, so that you only have to install what you really need for your particular application.
Stratego/XT.
All Stratego/XT users need to install the ATerm Library
(aterm), the SDF2 Bundle
(sdf2-bundle) and Stratego/XT
(strategoxt). These packages enable you to
compile Stratego programs, and provide the basic
infrastructure for parsing and pretty-printing source files.
Stratego Shell. Optionally, you can install the Stratego Shell, which provides an interpreter for Stratego and an interactive command-line for experimenting with the Stratego language. The Stratego Shell is used in the Stratego part of this tutorial to demonstrate the features of the Stratego language. The Stratego Shell is also very useful for small experiments with strategies of the Stratego Library.
Extensions. Then there are the language-specific packages. These packages provide the basic infrastructure for parsing, pretty-printing, and in some cases also analyzing source files of a specific programming language. Reusing such a package enables you to get started immediately with the implementation of an actual transformation. Examples of such packages are Java-front, Dryad, Transformers C and C++, BibTeX Tools, Prolog Tools, AspectJ Front, and SQL Front. Also, there are some demonstration packages, for example Tiger Base, which implements a compiler for the Tiger language, and Java Borg, which demonstrates the implementation of language embeddings. All these packages can separately be installed as extensions of Stratego/XT.
Examples of the Stratego/XT Manual. All the code examples in this manual are available for separate download, so that you can experiment based on these: examples.tar.gz
First of all, you have to decide which deployment mechanism you want to use. For users of RPM-based Linux distributions (such as Redhat, Fedora Core, and SUSE), we advise to use RPMs, which are available from the release page. For Cygwin users we provide pre-compiled binaries that can simply be unpacked. For Mac OS X users, we provide these binary packages as well, but they can also use the Nix deployment system, which will guarantee that all dependencies are installed correctly. Nix packages are also available for Linux users. Finally, it is always possible to build from source.
Next, download the required packages. Stratego/XT depends on the
ATerm Library and the SDF2 Bundle, so you have to download
aterm, sdf2-bundle, and
strategoxt. The downloads are all available at the
release page of Stratego/XT.
The following sequence of commands takes care of building
and installing the aterm and the sdf2-bundle in
/usr/local.
$tar zxf aterm-version.tar.gz$cd aterm-version$./configure$make$make install$cd ..$tar zxf sdf2-bundle-version.tar.gz$cd sdf2-bundle-version$./configure$make$make install$cd ..
If you want to install the packages at a different
location (i.e. not /usr/local, you
should specify a --prefix in the configure
command. For example:
$./configure --prefix=/opt/aterm$./configure --prefix=/opt/sdf2-bundle --with-aterm=/opt/aterm
In this case, it possible that the sdf2-bundle cannot find
the aterm package. To tell the sdf2-bundle where it should
look for the ATerm Library, you can use the
--with-aterm argument:
$ ./configure --prefix=/opt/sdf2-bundle --with-aterm=/opt/aterm
Alternatively, you can add the location of the ATerm
Library to the PKG_CONFIG_PATH, which the
configure script will use for searching packages. In this
way, you don't need to specify the --with-
arguments. More information about this is available in the
pkg-config documentation (man
pkg-config). For example:
$ export PKG_CONFIG_PATH=/opt/aterm/lib/pkgconfig:/opt/sdf2-bundle/lib/pkgconfig
Unpack, configure, make and install Stratego/XT using the following commands:
$tar zxf strategoxt-version.tar.gz$cd strategoxt-version$./configure$make$make install
If you want to install StrategoXT at a different prefix,
you should specify a --prefix. If you
installed the ATerm Library and the SDF2 Bundle at a
different location, you should specify their location
using --with-aterm and
--with-sdf. For example:
$ ./configure --prefix=/opt/strategoxt \
--with-aterm=/opt/aterm --with-sdf=/opt/sdf2-bundle
As mentioned earlier, you can alternatively add the
location of the ATerm Library and the SDF2 Bundle to the
PKG_CONFIG_PATH, which the configure script
will use for searching packages.
The Stratego Shell, Java Front, Tiger Base and several other packages depend on Stratego/XT. For all these packages, you can use the following commands:
$tar zxfpackage-version.tar.gz$cdpackage-version$./configure$make$make install
For all these packages, you should use the
--with-aterm=,
dir--with-sdf=,
and
dir--with-strategoxt=
options if you installed these packages at non-standard
locations. Alternatively, you can extend the
dirPKG_CONFIG_PATH to include the locations of
the ATerm Library, SDF2 Bundle, and Stratego/XT.
Installing binary RPMs is very easy. Install the RPMs by
running rpm -i * in the directory where you
have downloaded the RPMs. Use the upgrade option rpm
-U * if you have already installed earlier versions
of RPMs for aterm, strategoxt or the sdf2-bundle. Of course
you can also install the RPMs one by one by specifying the
filenames of the RPMs.
Using the Nix deployment system for the installation of Stratego/XT is a good idea if you need to run multiple versions of Stratego/XT on the same system, if you will need to update other Stratego/XT related packages regularly, or if there is a problem with installation from source at your system. The Nix deployment system is designed to guarantee that the Stratego/XT that we are using on our system is exactly reproduced on your system. This basically guarantees that the installation will never fail because of missing dependencies or mistakes in the configuration.
The release page of all the packages refer to Nix packages
that can be installed using
nix-install-package.
Table of Contents
- 3. Architecture
- 4. Annotated Terms
- 5. Syntax Definition and Parsing
- 6. Syntax Definition in SDF
- 7. Advanced Topics in Syntax Definition (*)
- 8. Trees, Terms, and Tree Grammars (*)
- 9. Pretty Printing with GPP (*)
Table of Contents
In this chapter, a general overview is given of the architecture of the XT transformation tools. The technical details of the tools and languages that are involved will be discussed in the follwing chapters.
XT is a collection of components for implementing transformation systems. Some of these components generate code that can be included in a transformation system, such as a parser or pretty-printer. Other components can be used immediately, since they are generic tools. The components of XT are all executable tools: they can be used directly from the command-line.
According to the Unix philosophy, the tools that are part of XT all do just one thing (i.e. implement one aspect of a transformation system) and can be composed into a pipeline to combine them in any way you want. A sketch of a typical pipeline is shown in Figure 3.1. First, a parser is applied to a source program. This results in an abstract syntax tree, which is then transformed by a sequence of transformation tools. Finally, the tree is pretty-printed back to a source program. So, this pipeline is a source to source transformation system. The tools that are part of the pipeline exchange structured representations of a program, in the form of an abstract syntax tree. These structured representations can be read in any programming language you want, so the various components of a transformation system can be implemented in different programming languages. Usually, the real transformation components will be implemented in Stratego.
Of course, some compositions are very common. For example, you definitly don't want to enter the complete pipeline of a compiler again and again. So, you want to pre-define such a composition to make it reusable as single tool. For this, you could of create a shell script, but option handling in shell scripts is quite tiresome and you cannot easily add composition specific glue code. To solve this, Stratego itself has a concise library for creating compositions of transformation tools, called XTC. We will come back to that later in Chapter 28.
The nice thing about this approach is that all the tools can be reused in different transformation systems. A parser, pretty-printer, desugarer, optimizer, simplifier, and so an is automatically available to other transformation systems that operate on the same language. Even if a tool will typically be used in a single dominant composition (e.g. a compiler), having the tool available to different transformation systems is very useful. In other words: an XT transformation system is open and its components are reusable.
Programmers write programs as texts using text editors. Some programming environments provide more graphical (visual) interfaces for programmers to specify certain domain-specific ingredients (e.g., user interface components). But ultimately, such environments have a textual interface for specifying the details. So, a program transformation system needs to deal with programs that are in text format.
However, for all but the most trivial transformations, a structured, rather than a textual, representation is needed. Working directly on the textual representation does not give the transformation enough information about what the text actually means. To bridge the gap between the textual and the structured representation, parsers and unparsers are needed. Also, we need to know how this structured representation is actually structured.
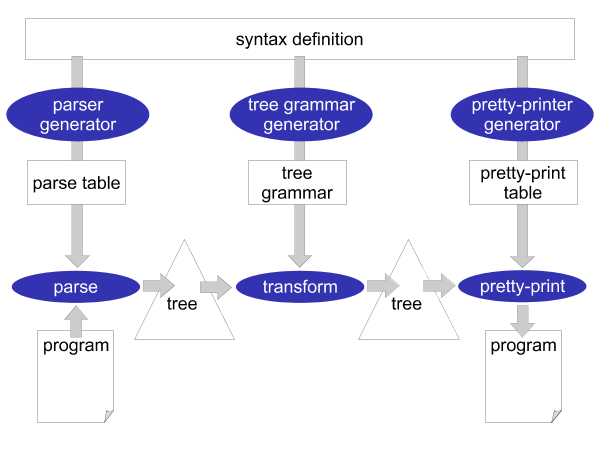
The syntactical rules of a programming language are usually expressed in a context-free grammar. This grammar (or syntax definition) of a programming language plays a central role in Stratego/XT. Most of the XT tools work on a grammar in one way or another. The grammar is a rich source of information. For example, it can be used to generate a parser, pretty-printer, disambiguator, tree grammar, format-checker, and documentation. This central role of a grammar is the most crucial aspect of XT, which is illustrated in Figure 3.2: all the components of a transformation system are directly or indirectly based on the grammar of a programming language.
What makes this all possible is the way syntax is defined in Stratego/XT. Stratego/XT uses the SDF language for syntax definition, which is a very high-level and declarative language for this purpose. SDF does not require the programmer to encode all kinds of properties of a programming language (such as associativity and priorities) in a grammar. Instead, SDF has declarative, concise, ways of defining these properties in such a way that they can actually be understood by tools that take the grammar as an input. And, of course, creating a grammar in such language is much more fun!
As mentioned before, the XT tools exchange a structured representation of a program: an abstract syntax tree. The structure of this abstract syntax tree is called the abstract syntax, as opposed to the ordinary textual syntax, which is called the concrete syntax. In XT, the abstract syntax is directly related to the syntax definition and can be generated from it. The result is a tree grammar that defines the format of the trees that are exchanged between the transformation tools. From the world of XML, you are probably already familiar with tree grammars: DTD, W3C XML Schema and RELAX NG are tree grammars in disguise.
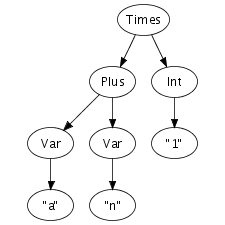
Until now, we have been a bit vague about the format in which abstract syntax trees are actually exchanged between transformation tools. What is this structured program representation?
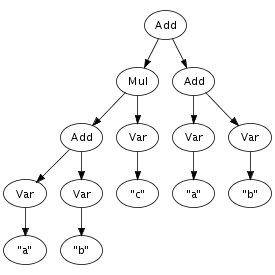
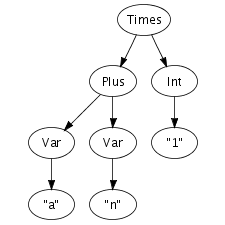
We can easily imagine an abstract syntax tree as a graphical
structure. For example, the tree at the right is a simple
abstract syntax tree for the expression (a + n) *
1. This representation corresponds closely to the
representation of trees in computer memory. However, drawing
pictures is not a very effective way of specifying tree
transformations. We need a concise, textual, way to express an
abstract syntax tree. Fortunately, there is a one-to-one
correspondence between trees and so-called first-order prefix
terms (terms, for short). A term is a constructor, i.e., an
identifier, applied to zero or more terms. Strings and integer
constants are terms as well. Thus, the following term
corresponds to the abstract syntax tree that we have just drawn.
Times(Plus(Var("a"), Var("n")), Int("1"))
In Stratego/XT, programs are exchanged between transformation tools as terms. The exact format we use for terms, is the Annotated Term Format, or ATerms for short. We will discuss this format in more detail later, but some of its features are interesting to note here.
First, ATerms are not only used to exchange programs between tools. ATerms are also used in the Stratego language itself for the representation of programs. In other words, ATerms are used for the external representation as well as the internal representation of programs in Stratego/XT. This is very convenient, since we don't have to bind the ATerms to Stratego specific data-structures. Usually, if such a data-binding is necessary, then there is always a mismatch here and there.
Second, an important feature of the implementation is that terms are represented using maximal sharing. This means that any term in use in a program is represented only once. In other words, two occurrences of the same term will be represented by pointers to the same location. This greatly reduces the amount of memory needed for representing programs.
Table of Contents
The Annotated Term Format, or ATerms for short, is heavily used in Stratego/XT. It used for the structured representation of programs (and also data in general). Program representations are exchanged between transformation tools in the ATerm format and the data-structures of the Stratego language itself are ATerms.
Before we start with the more interesting tools of XT, we need to take a closer look at the ATerm format. This chapter introduces the ATerm format and some tools that operate on ATerms.
The ATerm format provides a set of constructs for representing
trees, comparable to XML or abstract data types in functional
programming languages. For example, the code 4 + f(5 *
x) might be represented in a term as:
Plus(Int("4"), Call("f", [Mul(Int("5"), Var("x"))]))ATerms are constructed from the following elements:
- Integer
-
An integer constant, that is a list of decimal digits, is an ATerm. Examples:
1,12343. - String
-
A string constant, that is a list of characters between double quotes is an ATerm. Special characters such as double quotes and newlines should be escaped using a backslash. The backslash character itself should be escaped as well.
Examples:
"foobar","string with quotes\"","escaped escape character\\ and a newline\n". - Constructor application
-
A constructor is an identifier, that is an alphanumeric string starting with a letter, or a double quoted string.
A constructor application
c(t1,...,tn)creates a term by applying a constructor to a list of zero or more terms. For example, the termPlus(Int("4"),Var("x"))uses the constructorsPlus,Int, andVarto create a nested term from the strings"4"and"x".When a constructor application has no subterms the parentheses may be omitted. Thus, the term
Zerois equivalent toZero(). Some people consider it good style to explicitly write the parentheses for nullary terms in Stratego programs. Through this rule, it is clear that a string is really a special case of a constructor application. - List
-
A list is a term of the form
[t1,...,tn], that is a list of zero or more terms between square brackets.While all applications of a specific constructor typically have the same number of subterms, lists can have a variable number of subterms. The elements of a list are typically of the same type, while the subterms of a constructor application can vary in type.
Example: The second argument of the call to
"f"in the termCall("f",[Int("5"),Var("x")])is a list of expressions. - Tuple
-
A tuple
(t1,...,tn)is a constructor application without constructor. Example:(Var("x"), Type("int")) - Annotation
-
The elements defined above are used to create the structural part of terms. Optionally, a term can be annotated with a list terms. These annotations typically carry additional semantic information about the term. An annotated term has the form
t{t1,...,tn}. Example:Lt(Var("n"),Int("1")){Type("bool")}. The contents of annotations is up to the application.
As a Stratego programmer you will be looking a lot at raw ATerms. Stratego pioneers would do this by opening an ATerm file in emacs and trying to get a sense of the structure by parenthesis highlighting and inserting newlines here and there. These days your life is much more pleasant through the tool pp-aterm, which adds layout to a term to make it readable. For example, parsing the following program
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n - 1))
in printint(fact(10))
end
produces the following ATerm (say in file fac.trm):
Let([FunDecs([FunDec("fact",[FArg("n",Tp(Tid("int")))],Tp(Tid("int")),
If(Lt(Var("n"),Int("1")),Int("1"),Seq([Times(Var("n"),Call(Var("fact"),
[Minus(Var("n"),Int("1"))]))])))])],[Call(Var("printint"),[Call(Var(
"fact"),[Int("10")])])])
By pretty-printing the term using pp-aterm as
$ pp-aterm -i fac.trm
we get a much more readable term:
Let(
[ FunDecs(
[ FunDec(
"fact"
, [FArg("n", Tp(Tid("int")))]
, Tp(Tid("int"))
, If(
Lt(Var("n"), Int("1"))
, Int("1")
, Seq(
[ Times(
Var("n")
, Call(
Var("fact")
, [Minus(Var("n"), Int("1"))]
)
)
]
)
)
)
]
)
]
, [ Call(
Var("printint")
, [Call(Var("fact"), [Int("10")])]
)
]
)
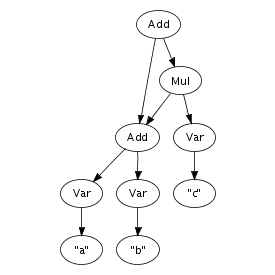
An important feature of the implementation is that terms are represented using maximal sharing. This means that any term in use in a program is represented only once. In other words, two occurrences of the same term will be represented by pointers to the same location. Figure 4.1 illustrates the difference between a pure tree representation and a tree, or more accurately, a directed acyclic graph, with maximal sharing. That is, any sub-term is represented exactly once in memory, with each occurrence pointing to the same memory location. This representation entails that term equality is a constant operation, since it consists of comparing pointers.
It should be noted that annotations create different terms, that is, two terms, one with and the other without annotations that are otherwise, modulo annotations, the same, are not equal.
Maximal sharing can make a big difference in the amount of bytes needed for representing programs. Therefore, we would like to preserve this maximal sharing when an ATerm is exchanged between two programs. When exporting a term using the textual exchange format, this compression is lost. Therefore, the ATerm Library also provides a binary exchange format that preserves maximal sharing.
Actually, there are three different formats:
- Textual ATerm Format
-
In the textual ATerm format the ATerm is written as plain text, without sharing. This format is very inefficient for the exchange of large programs, but it is readable for humans.
- Binary ATerm Format
-
The binary ATerm format, also known as BAF, is an extremely efficient binary encoding of an ATerm. It preserves maximal sharing and uses all kinds of tricks to represent an ATerm in as few bytes as possible.
- Shared Textual ATerm Format
-
In the shared, textual, format the ATerm is written as plain text, but maximal sharing is encoded in the text.
The tool baffle can be used to convert an ATerm from one format to another. Baffle, and other tools that operate on ATerms, automatically detect the format of an input ATerm.
The ATerm Format is an external representation for terms that can be used to exchange structured data between programs. In order to use a term, a program needs to parse ATerms and transform them into some internal representation. To export a term after processing it, a program should transform the internal representation into the standard format. There are libraries supporting these operation for a number of languages, including C, Java, and Haskell.
The implementation of the Stratego transformation language is based on the C implementation of the library. The library provides term input and output, and an API for constructing and inspecting terms. Garbage collection is based on Boehms conservative garbage collection algorithm.
Table of Contents
In Chapter 3 we have introduced the architecture of the XT tansformation tools. Source to source transformation systems based on XT consist of a pipeline of a parser, a series of transformations on a structured program representation, and a pretty-printer. In Chapter 4 we have explained the ATerm format, which is the format we use for this structured program transformation. This chapter will be about the parser part of the pipeline.
Stratego/XT uses the Syntax Definition Formalism (SDF), for defining the syntax of a programming language. From a syntax definition in SDF, a parser can be generated fully automatically. There is no need for a separate lexer or scanner specification, since SDF integrates the lexical and the context-free syntax definition of a programming language in a single specification. The generated parser is based on the Scannerless Generalized-LR algorithm, but more details about that later. The parser directly produces an ATerm representation of the program, as a parse tree, or as an abstract syntax tree.
Actually, the component-based approach of XT allows you to use any tool for parsing a source program to an ATerm. So, you don't necessarily have to use the parsing tools we present in this chapter. Instead, it might sometimes be a good idea to create an ATerm backend for a parser that you already have developed (by hand or using a different parser generator), or reuse an entire, existing front-end that is provided by a third-party. However, the techniques we present in this chapter are extremely expressive, flexible, and easy to use, so for developing a new parser it would be a very good idea to use SDF and SGLR.
In this section, we review the basics of grammars, parse trees and abstract syntax trees. Although you might already be familiar with these basic concepts, the perspective from the Stratego/XT point of view might still be interesting to read.
Context-free grammars were originally introduced by Chomsky to describe the generation of grammatically correct sentences in a language. A context-free grammar is a set of productions of the form A0 -> A1 ... An, where A0 is non-terminal and A1 ... An is a string of terminals and non-terminals. From this point of view, a grammar describes a language by generating its sentences. A string is generated by starting with the start non-terminal and repeatedly replacing non-terminal symbols according to the productions until a string of terminal symbols is reached.
A context-free grammar can also be used to recognize sentences in the language. In that process, a string of terminal symbols is rewritten to the start non-terminal, by repeatedly applying grammar productions backwards, i.e. reducing a substring matching the right-hand side of a production to the non-terminal on the left-hand side. To emphasize the recognition aspect of grammars, productions are specified as A1 ... An -> A0 in SDF.
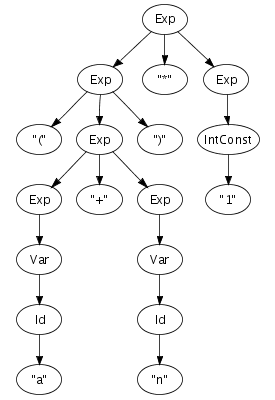
As an example, consider the SDF productions for a small language
of arithmetic expressions in Figure 5.1, where Id
and IntConst are terminals and Var and
Exp are non-terminals. Using this definition, and
provided that a and n are identifiers
(Id) and 1 is an
IntConst, a string such as (a+n)*1 can
be recognized as an expression by reducing it to
Exp, as shown by the reduction sequence in the
right-hand side of Figure 5.1.
Figure 5.1. Context-free productions and a reduction sequence.
Id -> Var
Var -> Exp
IntConst -> Exp
"-" Exp -> Exp
Exp "*" Exp -> Exp
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
"(" Exp ")" -> Exp
|
(a + n ) * 1 -> (Id + n ) * 1 -> (Var + n ) * 1 -> (Exp + n ) * 1 -> (Exp + Id ) * 1 -> (Exp + Var) * 1 -> (Exp + Exp) * 1 -> (Exp ) * 1 -> Exp * 1 -> Exp * IntConst -> Exp * Exp -> Exp |
Recognition of a string only leads to its grammatical category, not to any other information. However, a context-free grammar not only describes a mapping from strings to sorts, but actually assigns structure to strings. A context-free grammar can be considered as a declaration of a set of trees of one level deep. For example, the following trees correspond to productions from the syntax definition in Figure 5.1:
Such one-level trees can be composed into larger trees by fusing
trees such that the symbol at a leaf of one tree matches with
the root symbol of another, as is illustrated in the fusion of
the plus and times productions on the right.
The fusion process can continue as long as the tree has
non-terminal leaves. A tree composed in this fashion is a parse
tree if all leaves are terminal symbols. Figure 5.2 shows a parse tree for the expression
(a+n)*1, for which we showed a reduction sequence
earlier in Figure 5.1. This
illustrates the direct correspondence between a string and its
grammatical structure. The string underlying a parse tree can be
obtained by concatening the symbols at its leaves, also known as
the yield.
Parse trees can be derived from the reduction sequence induced by the productions of a grammar. Each rewrite step is associated with a production, and thus with a tree fragment. Instead of replacing a symbol with the non-terminal symbol of the production, it is replaced with the tree fragment for the production fused with the trees representing the symbols being reduced. Thus, each node of a parse tree corresponds to a rewrite step in the reduction of its underlying string. This is illustrated by comparing the reduction sequence in Figure 5.1 with the tree in Figure 5.2
The recognition of strings described by a syntax definition, and the corresponding construction of parse trees can be done automatically by a parser, which can be generated from the productions of a syntax definition.
Parse trees contain all the details of a program including
literals, whitespace, and comments. This is usually not
necessary for performing transformations. A parse tree is
reduced to an abstract syntax tree by
eliminating irrelevant information such as literal symbols and
layout. Furthermore, instead of using sort names as node labels,
constructors encode the production from
which a node is derived. For this purpose, the productions in a
syntax definition are extended with constructor
annotations. Figure 5.3 shows
the extension of the syntax definition from Figure 5.1 with constructor
annotations and the abstract syntax tree for the same good old
string (a+n)*1. Note that some identifiers are used
as sort names and and as constructors. This
does not lead to a conflict since sort names and constructors
are derived from separate name spaces. Some productions do not
have a constructor annotation, which means that these
productions do not create a node in the abstract syntax tree.
Figure 5.3. Context-free productions with constructor annotations and an abstract syntax tree.
Id -> Var {cons("Var")}
Var -> Exp
IntConst -> Exp {cons("Int")}
"-" Exp -> Exp {cons("Uminus")}
Exp "*" Exp -> Exp {cons("Times")}
Exp "+" Exp -> Exp {cons("Plus")}
Exp "-" Exp -> Exp {cons("Minus")}
Exp "=" Exp -> Exp {cons("Eq")}
Exp ">" Exp -> Exp {cons("Gt")}
"(" Exp ")" -> Exp
|  |
In the next section we will take a closer look at the various features of the SDF language, but before that it is useful to know your tools, so that you can immediately experiment with the various SDF features you will learn about. You don't need to fully understand the SDF fragments we use to explain the tools: we will come back to that later.
One of the nice things about SDF and the tools for it, is that the concepts that we have discussed directly translate to practice. For example, SDF supports all context-free grammars; the parser produces complete parse trees, which can even be yielded; parse trees can be converted to abstract syntax trees.
In SDF, you can split a syntax definition into multiple
modules. So, a complete syntax definition consists of a set
modules. SDF modules are stored in files with the extension
.sdf. Figure 5.4 shows
two SDF modules for a small language of expressions. The module
Lexical defines the identifiers and integer
literals of the language. This module is imported by the module
Expression.
Figure 5.4. SDF modules for a small language of arithmetic expressions.
module Expression
imports
Lexical Operators
exports
context-free start-symbols Exp
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")}
"(" Exp ")" -> Exp {bracket}
|
module Operators
exports
sorts Exp
context-free syntax
Exp "*" Exp -> Exp {left, cons("Times")}
Exp "/" Exp -> Exp {left, cons("Div")}
Exp "%" Exp -> Exp {left, cons("Mod")}
Exp "+" Exp -> Exp {left, cons("Plus")}
Exp "-" Exp -> Exp {left, cons("Minus")}
context-free priorities
{left:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
|
module Lexical
exports
sorts Id IntConst
lexical syntax
[\ \t\n] -> LAYOUT
[a-zA-Z]+ -> Id
[0-9]+ -> IntConst
|
Before you can invoke the parser generator to create a parser
for this expression language, the modules that constitute a
complete syntax definition have to be collected into a single
file, usually called a definition. This
file has the extension .def. Collecting SDF
modules into a .def file is the job of the
tool pack-sdf.
$ pack-sdf -i Expression.sdf -o Expression.def
Pack-sdf collects all modules imported by the SDF module
specified using the -i parameter. This results in a
combined syntax definition, which is written to the file
specified with the -o parameter. Modules are looked
for in the current directory and any of the include directories
indicated with the -I dir arguments.
Pack-sdf does not analyse the contents of an SDF module to report possible errors (except for syntactical ones). The parser generator, discussed next, performs this analysis.
Standard options for input and output
All tools in Stratego/XT use the -i and
-o options for input and output. Also, most tools
read from the standard input or write to standard output if no
input or output is specified.
From the .def definition file (as produced by
pack-sdf), the parser
generator sdf2table constructs
a parse table. This parse table can later on be handed off to
the actual parser.
$ sdf2table -i Expression.def -o Expression.tbl -m Expression
The -m option is used to specify the module for
which to generate a parse table. The default module is
Main, so if the syntax definition has a different
main module (in this case Expression), then you
need to specify this option.
The parse table is stored in a file with extension
.tbl. If all you plan on doing with your grammar is
parsing, the resulting .tbl file is all you need to
deploy. sdf2table could be thought of as a
parse-generator; however, unlike many other parsing systems, it
does not construct an parser program, but a compact data
representation of the parse table.
Sdf2table analyzes the SDF syntax definition to detect possible
errors, such as undefined symbols, symbols for which no
productions exists, deprecated features, etc. It is a good idea
to try to fix these problems, although sdf2table
will usually still happily generated a parse table for you.
Now we have a parse table, we can invoke the actual parser with
this parse table to parse a source program. The parser is called
sglr and produces a
complete parse tree in the so-called AsFix
format. Usually, we are not really interested in the parse tree
and want to work on an abstract syntax tree. For this, there is
the somewhat easier to use tool sglri,
which indirectly just invokes sglr.
$cat mul.exp (a + n) * 1$sglri -p Expression.tbl -i mul.exp Times(Plus(Var("a"),Var("n")),Int("1"))
For small experiments, it is useful that sglri can also read the source file from standard input. Example:
$ echo "(a + n) * 1" | sglri -p Expression.tbl
Times(Plus(Var("a"),Var("n")),Int("1"))
Heuristic Filters. As we will discuss later, SGLR uses disambiguation filters to select the desired derivations if there are multiple possibilities. Most of these filters are based on specifications in the original syntax definition, such a associativity, priorities, follow restrictions, reject, avoid and prefer productions. However, unfortunately there are some filters that select based on heuristics. Sometimes these heuristics are applicable to your situation, but sometimes they are not. Also, the heuristic filters make it less clear when and why there are ambiguities in a syntax definition. For this reason, they are disabled by default if you use sglri, (but not yet if you use sglr).
Start Symbols.
If the original syntax definition contained multiple start
symbols, then you can optionally specify the desired start
symbol with the -s option. For example, if we add
Id to the start-symbols of our
expression language, then a single identifier is suddenly an
ambiguous input (we will come back to ambiguities later) :
$ echo "a" | sglri -p Expression.tbl
amb([Var("a"),"a"])
By specifying a start symbol, we can instruct the parser to give us the expression alternative, which is the first term in the list of two alternatives.
$ echo "a" | sglri -p Expression.tbl -s Exp
Var("a")Working with Parse Trees. If you need a parse tree, then you can use sglr itself. These parse trees contain a lot of information, so they are huge. Usually, you really don't want to see them. Still, the structure of the parse tree is quite interesting, since you can exactly inspect how the productions from the syntax definition have been applied to the input.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | pp-aterm
parsetree( ... )
Note that we passed the options -2 -fi -fe to
sglr. The -2 option specifies the
variant of the AsFix parse tree format that should be used:
AsFix2. The Stratego/XT tools use this variant at the
moment. All variants of the AsFix format are complete and
faithful representation of the derivation constructed by the
parser. It includes all details of the input file, including
whitespace, comments, and is self documenting as it uses the
complete productions of the syntax definition to encode node
labels. The AsFix2 variant preserves all the structure of the
derivation. In the other variant, the structure of the lexical
parts of a parse tree are not preserved. The -fi
-fe options are used to heuristic disambiguation filters,
which are by default disabled in sglri, but not in
sglr.
The parse tree can be imploded to an abstract syntax tree
using the tool implode-asfix. The
combination of sglr and
implode-asfix has the same effect as directly
invoking sglri.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | implode-asfix
Times(Plus(Var("a"),Var("n")),Int("1"))The parse tree can also be yielded back to the original source file using the tool asfix-yield. Applying this tool shows that whitespace and comments are indeed present in the parse tree, since the source is reproduced in exactly the same way as it was!
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | asfix-yield
(a + n) * 1Table of Contents
First, basic structure of SDF. Second, how syntax is defined SDF. Third, examples of lexical and context-free syntax. Fourth, more detailed coverage of disambigation.
In this section, we give an overview of the basic constructs of SDF. After this section, you will now the basic idea of SDF. The next sections will discuss these constructs more detail.
Before defining some actual syntax, we have to explain the basic structure of a module. For this, let's take a closer look at the language constructs that are used in the modules we showed earlier in Figure 5.4.
Example 6.1. Basic constructs of SDF
module Expressionimports Lexical Operators
exports
context-free start-symbol Exp
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")} "(" Exp ")" -> Exp {bracket} module Operators exports sorts Exp
context-free syntax Exp "*" Exp -> Exp {left, cons("Times")}
Exp "/" Exp -> Exp {left, cons("Div")} Exp "%" Exp -> Exp {left, cons("Mod")} Exp "+" Exp -> Exp {left, cons("Plus")} Exp "-" Exp -> Exp {left, cons("Minus")} context-free priorities
{left: Exp "*" Exp -> Exp Exp "/" Exp -> Exp Exp "%" Exp -> Exp } > {left: Exp "+" Exp -> Exp Exp "-" Exp -> Exp } module Lexical exports sorts Id IntConst
lexical syntax
[a-zA-Z]+ -> Id [0-9]+ -> IntConst [\ \t\n] -> LAYOUT lexical restrictions
Id -/- [a-zA-Z]
Example 6.1 shows these modules, highlighting some of the constructs that are important to know before we dive into the details of defining syntax.
Usually, parsing is performed in two phases. First, a lexical analysis phase splits the input in tokens, based on a grammar for the lexical syntax of the language. This lexical grammar is usually specified by a set of regular expressions that specifiy the tokens of the language. Second, a parser based on a grammar for the context-free syntax of the language performs the syntactic analysis. This approach has several disadvantages for certain applications, which won't discuss in detail for now. One of the most important disadvantages is that the combination of the two grammars is not a complete, declarative definition of the syntax of the language.
SDF integrates the definition of lexical and context-free syntax
in a single formalism, thus supporting the
complete description of the syntax of a
language in a single specification. All syntax, both lexical and
context-free, is defined by productions,
respectively in lexical syntax and
context-free syntax sections. Parsing of languages
defined in SDF is implemented by scannerless generalized-LR
parsing, which operates on individual characters instead of
tokens.
Expressive Power. Since lexical and context-free syntax are both defined by productions, there is actually no difference in the expressive power of the lexical and context-free grammar. Hence, lexical syntax can be a context-free language, instead of being restricted to a regular grammar, which is the case when using conventional lexical analysis tools based on regular expression. For example, this means that you can define the syntax of nested comments in SDF, which we will illustrate later. In practice, more important is that it is easier to define lexical syntax using productions than using regular expressions.
Layout. Then, why are there two different sections for defining syntax? The difference between these two kinds of syntax sections is that in lexical syntax no layout (typically whitespace and comments) is allowed between symbols. In contrast, in context-free syntax sections layout is allowed between the symbols of a production. We will explain later how layout is defined. The allowance of layout is the only difference between the two kinds of syntax sections.
In the Section 5.1 we recapped context-free grammars and productions, which have the form A0 -> A1 ... An, where A0 is non-terminal and A1 ... An is a string of terminals and non-terminals. Also, we mentioned earlier that the distinction between terminals and non-terminals is less useful in SDF, since only single characters are terminals if the lexical and context-free syntax are defined in a single formalism. For this reason, every element of a production, i.e. A0 ... An is called a symbol. So, productions take a list of symbols and produce another symbol.
There are two primary symbols:
- Sorts
-
Sorts are names for language specific constructs, such as
Exp,Id, andIntConst. These names are declared using the previously introducedsortsdeclaration and defined by productions. - Character Classes
-
A character class is set of characters. Character classes are specified by single characters, character ranges, and can be combined using set operators, such as complement, difference, union, intersection. Examples:
[abc],[a-z],[a-zA-Z0-9],~[\n]. We will discuss character classes in more detail in Section 6.2.4.
Of course, defining an entire language using productions that
can contain only sorts and character classes would be a lot of
work. For example, programming languages usually contain all
kinds of list constructs. Specification of lists with plain
context-free grammars requires several productions for each list
construct. SDF provides a bunch of regular expression operators
abbreviating these common patterns. In the following list,
A represents a symbol and c a
character.
-
"c0 ... cn" -
Literals are strings that must literally occur in the input, such as keywords (
if,while,class), literals (null,true) and operators (+,*). Literals can be written naturally as, for example,"while". Escaping of special characters will be discussed in ???. A*-
Zero or more symbols
A. Examples:Stm*,[a-zA-Z]* A+-
One or more symbols
A. Examples:TypeDec+,[a-zA-Z]+ {A0 A1}*-
Zero or more symbols
A0separated byA1. Examples:{Exp ","}*,{FormalParam ","}* {A0 A1}+-
One or more symbols
A0separated byA1. Examples:{Id "."}+,{InterfaceType ","}+ A?-
Optional symbol
A. Examples:Expr?,[fFdD]? A0 | A1-
Alternative of symbol
A0orA1. Example:{Expr ","}* | LocalVarDec (A0 ... An)-
Sequence of symbols
A0 ... An.
In order to define the syntax at the level of characters, SDF
provides character classes, which represent a set of characters
from which one character can be recognized during parsing. The
content of a character classes is a specification of single
characters or character ranges
(c0-c1). Letters
and digits can be written as themselves, all other characters
should be escaped using a slash,
e.g. \_. Characters can also be indicated by their
decimal ASCII code, e.g. \13 for linefeed. Some
often used non-printable characters have more mnemonic names,
e.g., \n for newline, \ for space and
\t for tab.
Character classes can be combined using set operations. The most
common one is the unary complement operator ~, e.g
~[\n]. Binary operators are the set difference
/, union \/ and intersection
/\.
Example 6.2. Examples of Character Classes
-
[0-9] -
Character class for digits: 0, 1, 2, 3, 4, 5, 6, 8, 9.
-
[0-9a-fA-F] -
Characters typically used in hexi-decimal literals.
-
[fFdD] -
Characters used as a floating point type suffix, typically in C-like languages.
-
[\ \t\12\r\n] -
Typical character class for defining whitespace. Note that SDF does not yet support \f as an escape for form feed (ASCII code 12).
-
[btnfr\"\'\\] -
Character class for the set of characters that are usually allowed as escape sequences in C-like programming languages.
-
~[\"\\\n\r] -
The set of characters that is typically allowed in string literals.
Until now, we have mostly discussed the design of SDF. Now, it's about time to see how all these fancy ideas for syntax definition work out in practice. In this and the next section, we will present a series of examples that explain how typical language constructs are defined in SDF. This first section covers examples of lexical syntax constructs. The next section will be about context-free syntax.
Before we can start with the examples of lexical constructs like
identifiers and literals, you need to know the basics of
defining whitespace. In SDF, layout is a special sort, called
LAYOUT. To define layout, you have to define
productions that produce this LAYOUT sort. Thus, to
allow whitespace we can define a production that takes all
whitespace characters and produces layout. Layout is lexical
syntax, so we define this in a lexical syntax section.
lexical syntax [\ \t\r\n] -> LAYOUT
We can now also reveal how context-free syntax
exactly works. In context-free syntax, layout is
allowed between symbols in the left-hand side of the
productions, by automatically inserting optional layout
(e.g. LAYOUT?) between them.
In the following examples, we will assume that whitespace is always defined in this way. So, we will not repeat this production in the examples. We will come back to the details of whitespace and comments later.
Almost every language has identifiers, so we will start with that. Defining identifiers themselves is easy, but there is some more definition of syntax required, as we will see next. First, the actual definition of identifiers. As in most languages, we want to disallow digits as the first character of an identifier, so we take a little bit more restrictive character class for that first character.
lexical syntax [A-Za-z][A-Za-z0-9]* -> Id
If a language would only consists of identifiers, then this
production does the job. Unfortunately, life is not that easy.
In practice, identifiers interact with other language
constructs. The best known interaction is that most languages
do not allow keywords (such as if,
while, class) and special literals
(such as null, true). In SDF,
keywords and special literals are not automatically preferred
over identifiers. For example, consider the following, very
simple expression language (for the context-free syntax we
appeal to your intuition for now).
lexical syntax
[A-Za-z][A-Za-z0-9]* -> Id
"true" -> Bool
"false" -> Bool
context-free start-symbols Exp
context-free syntax
Id -> Exp {cons("Id")}
Bool -> Exp {cons("Bool")}
The input true can now be parsed as an identifier
as well as a boolean literal. Since the generalized-LR parser
actually supports ambiguities, we can even try this out:
$ echo "true" | sglri -p Test.tbl
amb([Bool("true"), Id("true")])
The amb term is a representation of the
ambiguity. The argument of the ambiguity is a list of
alternatives. In this case, the first is the boolean literal
and the second is the identifier true. So, we have to define
explicitly that we do not want to allow these boolean literals
as identifiers. For this purpose, we can use SDF
reject productions. The intuition of
reject productions is that all
derivations of a symbol for which there is a reject production
are forbidden. In this example, we need to create productions
for the boolean literals to identifiers.
lexical syntax
"true" -> Id {reject}
"false" -> Id {reject}
For true, there will now be two derivations for
an Id: one using the reject production and one
using the real production for identifiers. Because of that
reject production, all derivations will be rejected, so
true is not an identifier anymore. Indeed, if we
add these productions to our syntax definition, then the true
literal is no longer ambiguous:
$ echo "true" | sglri -p Test.tbl
Bool("true")
We can make the definition of these reject productions a bit
more concise by just reusing the Bool sort. In
the same way, we can define keywords using separate production
rules and have a single reject production from keywords to
identifiers.
lexical syntax
Bool -> Id {reject}
Keyword -> Id {reject}
"class" -> Keyword
"if" -> Keyword
"while" -> Keyword
Scanners usually apply a longest match policy for scanning tokens. Thus, if the next character can be included in the current token, then this will always be done, regardless of the consequences after this token. In most languages, this is indeed the required behaviour, but in some languages longest match scanning actually doesn't work. Similar to not automatically reserving keywords, SDF doesn't choose the longest match by default. Instead, you need to specify explicitly that you want to recognize the longest match.
For example, suppose that we introduce two language constructs
based on the previously defined Id. The following
productions define two statements: a simple goto and a
construct for variable declarations, where the first
Id is the type and the second the variable name.
context-free syntax
Id -> Stm {cons("Goto")}
Id Id -> Stm {cons("VarDec")}
For the input foo, which is of course intended to
be a goto, the parser will now happily split up the identifier
foo, which results in variable
declarations. Hence, this input is ambiguous.
$ echo "foo" | sglri -p Test.tbl
amb([Goto("foo"), VarDec("f","oo"), VarDec("fo","o")])
To specify that we want the longest match of an identifier, we
define a follow restriction. Such a
follow restriction indicates that a string of a certain symbol
cannot be followed by a character from the given character
class. In this way, follow restrictions can be used to encode
longest match disambiguation. In this case, we need to specify
that an Id cannot be followed by one of the
identifier characters:
lexical restrictions Id -/- [A-Za-z0-9]
Indeed, the input foo is no longer ambiguous and
is parsed as a goto:
$ echo "foo" | sglri -p Test.tbl
Goto("foo")
In Section 6.3.2 we
explained how to reject keywords as identifiers, so we will not
repeat that here. Also, we discussed how to avoid that
identifiers get split. A similar split issue arises with
keywords. Usually, we want to forbid a letter immediately after
a keyword, but the scannerless parser will happily start a new
identifier token immediately after the keyword. To illustrate
this, we need to introduce a keyword, so let's make our previous
goto statement a bit more clear:
context-free syntax
"goto" Id -> Stm {cons("Goto")}
To illustrate the problem, let's take the input
gotox. Of course, we don't want to allow this
string to be a goto, but without a follow restriction, it will
actually be parsed by starting an identifier after the
goto:
$ echo "gotox" | sglri -p Test.tbl
Goto("x")
The solution is to specify a follow restriction on the
"goto" literal symbol.
lexical restrictions "goto" -/- [A-Za-z0-9]
It is not possible to define the follow restrictions on the
Keyword sort that we introduced earlier in the
reject example. The follow restriction must be
defined on the symbol that literally occurs
in the production, which is not the case with the
Keyword symbol. However, you can specify all the
symbols in a single follow restriction, seperated by spaces:
lexical restrictions "goto" "if" -/- [A-Za-z0-9]
Compared to identifiers, integer literals are usually very easy to define, since they do not really interact with other language constructs. Just to be sure, we still define a lexical restriction. The need for this restriction depends on the language in which the integer literal is used.
lexical syntax [0-9]+ -> IntConst lexical restrictions IntConst -/- [0-9]
In mainstream languages, there are often several notations for
integer literal, for example decimal, hexadecimal, or octal. The
alternatives are then usually prefixed with one or more
character that indicates the kind of integer literal. In Java,
hexadecimal numerals start with 0x and octal with a
0 (zero). For this, we have to make the definition
of decimal numerals a bit more precise, since 01234
is now an octal numeral.
lexical syntax "0" -> DecimalNumeral [1-9][0-9]* -> DecimalNumeral [0][xX] [0-9a-fA-F]+ -> HexaDecimalNumeral [0] [0-7]+ -> OctalNumeral
Until now, the productions for lexical syntax have not been very complex. In some cases, the definition of lexical syntax might even seem to be more complex in SDF, since you explicitly have to define behaviour that is implicit in existing lexical anlalysis tools. Fortunately, the expressiveness of lexical syntax in SDF also has important advantages, even if it is applied to language that are designed to be processed with a separate scanner. As a first example, let's take a look at the definition of floating-point literals.
Floating-point literals consists of three elements: digits,
which may include a dot, an exponent, and a float suffix
(e.g. f, d etc). There are three
optional elements in float literals: the dot, the exponent, and
the float suffix. But, if you leave them all out, then the
floating-point literal no longer distinguishes itself from an
integer literal. So, one of the floating-point specific elements
is required. For example, valid floating-point literals are:
1.0, 1., .1,
1f, and 1e5, but invalid are:
1, and .e5. These rules are encoded in
the usual definition of floating-point literals by duplicating
the production rule and making different elements optional and
required in each production. For example:
lexical syntax [0-9]+ "." [0-9]* ExponentPart? [fFdD]? -> FloatLiteral [0-9]* "." [0-9]+ ExponentPart? [fFdD]? -> FloatLiteral [0-9]+ ExponentPart [fFdD]? -> FloatLiteral [0-9]+ ExponentPart? [fFdD] -> FloatLiteral [eE] SignedInteger -> ExponentPart [\+\-]? [0-9]+ -> SignedInteger
However, in SDF we can use reject
production to reject these special cases. So, the
definition of floating-point literals itself can be more
naturally defined in a single production  . The reject production
. The reject production  defines that there
should at least be one element of a floating-point literal: it
rejects plain integer literals. The reject production
defines that there
should at least be one element of a floating-point literal: it
rejects plain integer literals. The reject production  defines that the digits part of the
floating-point literals is not allowed to be a single dot.
defines that the digits part of the
floating-point literals is not allowed to be a single dot.
lexical syntax FloatDigits ExponentPart? [fFdD]? -> FloatLiteral[0-9]* "." [0-9]* -> FloatDigits [0-9]+ -> FloatDigits [0-9]+ -> FloatLiteral {reject}
"." -> FloatDigits {reject}
Similar to defining whitespace, comments can be allowed
everywhere by defining additional LAYOUT
productions. In this section, we give examples of how to define
several kinds of common comments.
Most languages support end-of-line comments, which start with
special characters, such as //, #,
or %. After that, all characters on that line are
part of the comment. Defining end-of-line comments is quite
easy: after the initial characters, every character except for
the line-terminating characters is allowed until a line
terminator.
lexical syntax "//" ~[\n]* [\n] -> LAYOUT
Block comments (i.e. /* ... */) are a bit more
tricky to define, since the content of a block comment may
include an asterisk (*). Let's first take a look
at a definition of block comments that does not allow an
asterisk in its content:
"/*" ~[\*]* "*/" -> LAYOUT
If we allow an asterisk and a slash, the sequence
*/ will be allowed as well. So, the parser will
accept the string /* */ */ as a comment, which is
not valid in C-like languages. In general, allowing this in a
language would be very inefficient, since the parser can never
decide where to stop a block comment. So, we need to disallow
just the specific sequence of characters */
inside a comment. We can specify this using a follow
restriction: an asterisk in a block comments is
allowed, but it cannot be followed by a slash
(/).
But, on what symbol do we specify this follow restriction? As
explained earlier, we need to specify this follow restriction
on a symbol that literally occurs in the
production. So, we could try to allow a "*", and
introduce a follow restriction on that:
lexical syntax "/*" (~[\*] | "*")* "*/" -> LAYOUT lexical restrictions "*" -/- [\/]
But, the symbol "*" also occurs in other
productions, for example in multiplication expressions and we
do not explicitly say here that we intend to refer to the
"*" in the block comment production. To
distinguish the block comment asterisk from the multiplication
operator, we introduce a new sort, creatively named
Asterisk, for which we can specify a follow
restriction that only applies to the asterisk in a block
comment.
lexical syntax "/*" (~[\*] | Asterisk)* "*/" -> LAYOUT [\*] -> Asterisk lexical restrictions Asterisk -/- [\/]
To illustrate that lexical syntax in SDF can actually be
context-free, we now show an example of how to implement
balanced, nested block comments, i.e. a block comment that
supports block comments in its content: /* /* */
*/. Defining the syntax for nested block comments is
quite easy, since we can just define a production that allows
a block comment inside itself  . For performance and
predictability, it is important to require that the comments
are balanced correctly. So, in addition to disallowing
. For performance and
predictability, it is important to require that the comments
are balanced correctly. So, in addition to disallowing
*/ inside in block comments, we now also have to
disallow /*. For this, we introduce a
Slash sort, for which we define a follow
restriction  ,
similar to the
,
similar to the Asterisk sort that we discussed in
the previous section.
lexical syntax BlockComment -> LAYOUT "/*" CommentPart* "*/" -> BlockComment ~[\/\*] -> CommentPart Asterisk -> CommentPart Slash -> CommentPart BlockComment -> CommentPart[\/] -> Slash [\*] -> Asterisk lexical restrictions Asterisk -/- [\/] Slash -/- [\*]
Context-free syntax in SDF is syntax where layout is allowed between the symbols of the productions. Context-free syntax can be defined in a natural way, thanks to the use of generalized-LR parsing, declarative disambiguation mechanism, and an extensive set of regular expression operators. To illustrate the definition of context-free syntax, we give examples of defining expressions and statements. Most of the time will be spend on explaining the disambiguation mechanisms.
In the following sections, we will explain the details of a slightly extended version of the SDF modules in Example 6.1, shown in Example 6.3.
Example 6.3. Syntax of Small Expression Language in SDF
module Expression
imports
Lexical
exports
context-free start-symbols Exp
context-free syntax
Id -> Var 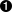 Var -> Exp {cons("Var")
Var -> Exp {cons("Var")  }
IntConst -> Exp {cons("Int")
}
IntConst -> Exp {cons("Int")  }}
"(" Exp ")" -> Exp {bracket
}}
"(" Exp ")" -> Exp {bracket  }
"-" Exp -> Exp {cons("UnaryMinus")}
Exp "*" Exp -> Exp {cons("Times"), left
}
"-" Exp -> Exp {cons("UnaryMinus")}
Exp "*" Exp -> Exp {cons("Times"), left  }
Exp "/" Exp -> Exp {cons("Div"), left}
Exp "%" Exp -> Exp {cons("Mod"), left}
Exp "+" Exp -> Exp {cons("Plus")
}
Exp "/" Exp -> Exp {cons("Div"), left}
Exp "%" Exp -> Exp {cons("Mod"), left}
Exp "+" Exp -> Exp {cons("Plus")  , left}
Exp "-" Exp -> Exp {cons("Minus"), left}
Exp "=" Exp -> Exp {cons("Eq"), non-assoc
, left}
Exp "-" Exp -> Exp {cons("Minus"), left}
Exp "=" Exp -> Exp {cons("Eq"), non-assoc  }
Exp ">" Exp -> Exp {cons("Gt"), non-assoc}
context-free priorities
}
Exp ">" Exp -> Exp {cons("Gt"), non-assoc}
context-free priorities  "-" Exp -> Exp
"-" Exp -> Exp  > {left:
> {left:  Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
> {non-assoc:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
> {non-assoc:  Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
}
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
}
First, it is about time to explain the constructor attribute,
cons, which was already briefly mentioned in Section 5.1.2. In the example
expression language, most productions have a constructor
attribute, for example 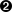 ,
,  and
and  ,
but some have not, for example
,
but some have not, for example  and
and  .
.
The cons attribute does not have any actual meaning
in the definition of the syntax, i.e the presence or absence of
a constructor does not affect the syntax that is defined in any
way. The constructor only serves to specify the name of the
abstract syntax tree node that is to be constructed if that
production is applied. In this way, the cons
attribute  of the production for
integer literals, defines that an
of the production for
integer literals, defines that an Int node should
be produced for that production:
$ echo "1" | sglri -p Test.tbl
Int("1")
Note that this Int constructor takes a single
argument, a string, which is the name of the variable. This
argument of Int is a string because the production
for IntConst is defined in lexical
syntax and all derivations from lexical syntax
productions are represented as strings, i.e. without
structure. As another example, the production for addition has a
Plus constructor attribute  . This production has three symbols on
the left-hand side, but the constructor takes only two
arguments, since literals are not included in the abstract
syntax tree.
. This production has three symbols on
the left-hand side, but the constructor takes only two
arguments, since literals are not included in the abstract
syntax tree.
$ echo "1+2" | sglri -p Test.tbl
Plus(Int("1"),Int("2"))
However, there are also productions that have no
cons attribute, i.e.  and
and  . The production
. The production  from
from Id to
Var is called an injection,
since it does not involve any additional syntax. Injections
don't need to have a constructor attribute. If it is left out,
then the application of the production will not produce a node
in the abstract syntax tree. Example:
$ echo "x" | sglri -p Test.tbl
Var("x")
Nevertheless, the production  does involve additional syntax, but does not have a
constructor. In this case, the
does involve additional syntax, but does not have a
constructor. In this case, the bracket attribute
should be used to indicate that this is a symbol between
brackets, which should be literals. The bracket
attribute does not affect the syntax of the language, similar to
the constructor attribute. Hence, the parenthesis in the
following example do not introduce a node, and the
Plus is a direct subterm of Times.
$ echo "(1 + 2) * 3" | sglri -p Test.tbl
Times(Plus(Int("1"),Int("2")),Int("3"))Conventions. In Stratego/XT, constructors are by covention CamelCase. Constructors may be overloaded, i.e. the same name can be used for several productions, but be careful with this feature: it might be more difficult to distinguish the several cases for some tools. Usually, constructors are not overloaded for productions with same number of arguments (arity).
Example 6.4. Ambiguous Syntax Definition for Expressions
Exp "+" Exp -> Exp {cons("Plus")}
Exp "-" Exp -> Exp {cons("Minus")}
Exp "*" Exp -> Exp {cons("Mul")}
Exp "/" Exp -> Exp {cons("Div")}
Syntax definitions that use only a single non-terminal for
expressions are highly ambiguous. Example 6.4 shows the basic arithmetic
operators defined in this way. For every combination of
operators, there are now multiple possible derivations. For
example, the string a+b*c has two possible
derivations, which we can actually see because of the use of a
generalized-LR parser:
$ echo "a + b * c" | sglri -p Test3.tbl | pp-aterm
amb(
[ Times(Plus(Var("a"), Var("b")), Var("c"))
, Plus(Var("a"), Times(Var("b"), Var("c")))
]
)
These ambiguities can be solved by using the associativities and
priorities of the various operators to disallow undesirable
derivations. For example, from the derivations of a + b *
c we usually want to disallow the second one, where the
multiplications binds weaker than the addition operator. In
plain context-free grammars the associativity and priority rules
of a language can be encoded in the syntax definition by
introducing separate non-terminals for all the priority levels
and let every argument of productions refer to such a specific
priority level. Example 6.5
shows how the usual priorities and associativity of the
operators of the example can be encoded in this way. For
example, this definition will never allow an AddExp
as an argument of a MulExp, which implies that
* binds stronger than +. Also,
AddExp can only occur at the left-hand side of an
AddExp, which makes the operator left associative.
This way of dealing with associativity and priorities has several disadvantages. First, the disambiguation is not natural, since it is difficult to derive the more high-level rules of priorities and associativity from this definition. Second, it is difficult to define expressions in a modular way, since the levels need to be known and new operators might affect the carefully crafted productions for the existing ones. Third, due to all the priority levels and the productions that connect these levels, the parse trees are more complex and parsing is less efficient. For these reasons SDF features a more declarative way of defining associativity and priorities, which we discuss in the next section.
Example 6.5. Non-Ambiguous Syntax Definition for Expressions
AddExp -> Exp
MulExp -> AddExp
AddExp "+" MulExp -> AddExp {cons("Plus")}
AddExp "-" MulExp -> AddExp {cons("Minus")}
PrimExp -> MulExp
MulExp "*" PrimExp -> MulExp {cons("Mul")}
MulExp "/" PrimExp -> MulExp {cons("Div")}
IntConst -> PrimExp {cons("Int")}
Id -> PrimExp {cons("Var")}
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
In order to support natural syntax definitions, SDF provides
several declarative disambiguation mechanisms. Associativity
declarations (left, right,
non-assoc), disambiguate combinations of a binary
operator with itself and with other operators. Thus, the left
associativity of + entails that a+b+c
is parsed as (a+b)+c. Priority declarations
(>) declare the relative priority of productions. A
production with lower priority cannot be a direct subtree of a
production with higher priority. Thus a+b*c is
parsed as a+(b*c) since the other parse
(a+b)*c has a conflict between the *
and + productions.
... > Exp "&" Exp -> Exp > Exp "^" Exp -> Exp > Exp "|" Exp -> Exp > Exp "&&" Exp -> Exp > Exp "||" Exp -> Exp > ...
This is usually handled with introducing a new non-terminal.
context-free syntax
"new" ArrayBaseType DimExp+ Dim* -> ArrayCreationExp {cons("NewArray")}
Exp "[" Exp "]" -> Exp {cons("ArrayAccess")}
ArrayCreationExp "[" Exp "]" -> Exp {reject}
Figure 6.1 illustrates the use of
these operators in the extension of the expression language with
statements and function declarations. Lists are used in numerous
places, such as for the sequential composition of statements
(Seq), the declarations in a let binding, and the
formal and actual arguments of a function (FunDec
and Call). An example function definition in this
language is:
Figure 6.1. Syntax definition with regular expressions.
module Statements
imports Expressions
exports
sorts Dec FunDec
context-free syntax
Var ":=" Exp -> Exp {cons("Assign")}
"(" {Exp ";"}* ")" -> Exp {cons("Seq")}
"if" Exp "then" Exp "else" Exp -> Exp {cons("If")}
"while" Exp "do" Exp -> Exp {cons("While")}
"let" Dec* "in" {Exp ";"}* "end" -> Exp {cons("Let")}
"var" Id ":=" Exp -> Dec {cons("VarDec")}
FunDec+ -> Dec {cons("FunDecs")}
"function" Id "(" {Id ","}* ")"
"=" Exp -> FunDec {cons("FunDec")}
Var "(" {Exp ","}* ")" -> Exp {cons("Call")}
context-free priorities
{non-assoc:
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp}
> Var ":=" Exp -> Exp
> {right:
"if" Exp "then" Exp "else" Exp -> Exp
"while" Exp "do" Exp -> Exp}
> {Exp ";"}+ ";" {Exp ";"}+ -> {Exp ";"}+
context-free start-symbols Exp
function fact(n, x) = if n > 0 then fact(n - 1, n * x) else x
Parse-unit is a tool, part of Stratego/XT, for testing SDF syntax definitions. The spirit of unit testing is implemented in parse-unit by allowing you to check that small code fragments are parsed correctly with your syntax definition.
In a parse testsuite you can define tests with an input and an
expected result. You can specify that a test should succeed
(succeeds, for lazy people), fail
(fails) or that the abstract syntax tree should have
a specific format. The input can be an inline string or the
contents of a file for larger tests.
Assuming the following grammar for a simple arithmetic expressions:
module Exp
exports
context-free start-symbols Exp
sorts Id IntConst Exp
lexical syntax
[\ \t\n] -> LAYOUT
[a-zA-Z]+ -> Id
[0-9]+ -> IntConst
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")}
Exp "*" Exp -> Exp {left, cons("Mul")}
Exp "/" Exp -> Exp {left, cons("Div")}
Exp "%" Exp -> Exp {left, cons("Mod")}
Exp "+" Exp -> Exp {left, cons("Plus")}
Exp "-" Exp -> Exp {left, cons("Minus")}
context-free priorities
{left:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
You could define the following parse testsuite in a file
expression.testsuite :
testsuite Expressions
topsort Exp
test simple int literal
"5" -> Int("5")
test simple addition
"2 + 3" -> Plus(Int("2"), Int("3"))
test addition is left associative
"1 + 2 + 3" -> Plus(Plus(Int("1"), Int("2")), Int("3"))
test
"1 + 2 + 3" succeeds
test multiplication has higher priority than addition
"1 + 2 * 3" -> Plus(Int("1"), Mul(Int("2"), Int("3")))
test
"x" -> Var("x")
test
"x1" -> Var("x1")
test
"x1" fails
test
"1 * 2 * 3" -> Mul(Int("1"), Mul(Int("2"), Int("3")))
Running this parse testsuite with:
$ parse-unit -i expression.testsuite -p Exp.tbl
will output:
-----------------------------------------------------------------------
executing testsuite Expressions with 9 tests
-----------------------------------------------------------------------
* OK : test 1 (simple int literal)
* OK : test 2 (simple addition)
* OK : test 3 (addition is left associative)
* OK : test 4 (1 + 2 + 3)
* OK : test 5 (multiplication has higher priority than addition)
* OK : test 6 (x)
sglr: error in g_0.tmp, line 1, col 2: character `1' (\x31) unexpected
* ERROR: test 7 (x1)
- parsing failed
- expected: Var("x1")
sglr: error in h_0.tmp, line 1, col 2: character `1' (\x31) unexpected
* OK : test 8 (x1)
* ERROR: test 9 (1 * 2 * 3)
- succeeded: Mul(Mul(Int("1"),Int("2")),Int("3"))
- expected: Mul(Int("1"),Mul(Int("2"),Int("3")))
-----------------------------------------------------------------------
results testsuite Expressions
successes : 7
failures : 2
-----------------------------------------------------------------------
You cannot escape special characters because there is no need to escape them. The idea of the testsuite syntax is that test input typically contains a lot of special characters, which therefore they should no be special and should not need escaping.
Anyhow, you still need some mechanism make it clear where the
test input stops. Therefore the testsuite syntax supports
several quotation symbols. Currently you can choose from:
", "", """, and
[, [[, [[[. Typically, if
you need a double quote in your test input, then you use the
[.
Parse-unit has an option to parse a single test and write the
result to the output. In this mode ambiguities are accepted,
which is useful for debugging. The option for the 'single test
mode' is --single
where nrnr is the number in the
testsuite (printed when the testsuite is executed). The
--asfix2 flag can be used to produce an asfix2
parse tree instead of an abstract syntax tree.
The following make rule can be used to invoke parse-unit from your build system.
%.runtestsuite : %.testsuite
$(SDF_TOOLS)/bin/parse-unit -i $< -p $(PARSE_UNIT_PTABLE) --verbose 1 -o /dev/null
A typical Makefile.am fo testing your
syntax definitions looks like:
EXTRA_DIST = $(wildcard *.testsuite)
TESTSUITES = \
expressions.testsuite \
identifiers.testsuite
PARSE_UNIT_PTABLE = $(top_srcdir)/syn/Foo.tbl
installcheck-local: $(TESTSUITES:.testsuite=.runtestsuite)
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
Import module and rename symbols in the imported definition.
Not very common, but heavily used for combining syntax definitions of different language. See concrete object syntax.
Modules can have formal parameters.
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
Format-check analyzes whether the input ATerm conforms to the format that is specified in the RTG (Regular Tree Grammar).
Format-check verifies that the input ATerm is part of the language defined in the RTG. If this is not the case, then the ATerm contains format errors. Format-check can operate in three modes: plain, visualize and XHTML.
The plain mode is used if the other modes are not enabled. In the plain mode format errors are reported and no result is written the the output (stdout or a file). Hence, if format-check is included in a pipeline, then the following tool will probably fail. If the input term is correct, then it is written to the output.
The visualize mode is enabled with the --vis
option. In visualize mode format errors are reported and in a
pretty-printed ATerm will be written to the output. All
innermost parts of the ATerm that cause format errors are
printed in red, if your terminal supports control characters
for colors. If you want to browse through the ATerm with less,
then you should use the -r flag.
The XHTML mode is enabled with the --xhtml
option. In XHTML mode format errors are reported and an report
in XHTML will be written to the output. This report shows the
parts of the ATerm that are not formatted correctly. Also,
moving with your mouse over the nodes of ATerm, will show the
non-terminals that have be inferred by format-check (do not use
IE6. Firefox or Mozilla is recommended).
Format-check reports all innermost format errors. That is, only the deepest format errors are reported. A format error is reported by showing the ATerm that is not in the correct format, and the inferred types of the children of the ATerm. In XHTML and visualize mode a format error of term in a list is presented by a red comma and term. This means that a type has been inferred for the term itself, but that it is not expected at this point in the list. If only the term is red, then no type could be inferred for the term itself.
In all modes format-check succeeds (exit code 0) if the ATerm contains no format errors. If the term does contain format errors, then format-check fails (exit code 1).
Consider the RTG generated in the example of sdf2rtg:
regular tree grammar
start Exp
productions
Exp -> Minus(Exp,Exp)
Exp -> Plus(Exp,Exp)
Exp -> Mod(Exp,Exp)
Exp -> Div(Exp,Exp)
Exp -> Mul(Exp,Exp)
Exp -> Int(IntConst)
Exp -> Var(Id)
IntConst -> <string>
Id -> <string>
The ATerm
Plus(Var("a"), Var("b"))
is part of the language defined by this RTG. Therefore, format-check succeeds:
$ format-check --rtg Exp.rtg -i exp1.trm
Plus(Var("a"),Var("b"))
$
Note that format-check outputs the input term in this case. In this way format-check can be used in a pipeline of tools. On the other hand, the ATerm
Plus(Var("a"), Var(1))
is not part of the language defined by this RTG. Therefore, the invocation of format-check fails. Format-check also reports which term caused the failure:
$ format-check --rtg Exp.rtg -i exp2.trm
error: cannot type Var(1)
inferred types of subterms:
typed 1 as <int>
$
In large ATerms it might be difficult to find the incorrect
subterm. To help with this, format-check supports the
--vis argument. If this argument is used, then the
result will pretty-printed (in the same way as pp-aterm) and the incorrect parts
will be printed in red.
For example, consider this term:
Plus(Mul(Int(1), Var("a")), Minus(Var("b"), Div(1, Var("c"))))
format-check will visualize the errors in this ATerm:

The XHTML mode shows the errors in red as well. Moreover, if you move your moves over the terms, then you'll see the inferred types of the term.
$ format-check --rtg Exp.rtg -i exp3.trm --xhtml -o foo.html
You can now view the resulting file in your browser. You need a decent browser (Firefox or Mozilla. no IE).
The abstract syntax of a programming language or data format can
be described by means of an algebraic
signature. A signature declares for each constructor
its arity m, the sorts of its arguments S1 *
... * Sm, and the sort of the resulting term
S0 by means of a constructor declaration c:S1 *
... * Sm -> S0. A term can be validated against a
signature by a format checker.
Signatures can be derived automatically from syntax definitions.
For each production A1...An -> A0 {cons(c)} in a
syntax definition, the corresponding constructor declaration is
c:S1 * ... * Sm -> S0, where the Si are
the sorts corresponding to the symbols Aj after
leaving out literals and layout sorts. Figure 8.1 shows the signatures of statement and
expression constructors for the example language from this
chapter. The modules have been derived automatically from the
syntax definitions in ??? and
Figure 6.1.
Figure 8.1. Signature for statement and expression constructors, automatically derived from a syntax definition.
module Statements
signature
constructors
FunDec : Id * List(Id) * Exp -> FunDec
FunDecs : List(FunDec) -> Dec
VarDec : Id * Exp -> Dec
Call : Var * List(Exp) -> Exp
Let : List(Dec) * List(Exp) -> Exp
While : Exp * Exp -> Exp
If : Exp * Exp * Exp -> Exp
Seq : List(Exp) -> Exp
Assign : Var * Exp -> Exp
Gt : Exp * Exp -> Exp
Eq : Exp * Exp -> Exp
Minus : Exp * Exp -> Exp
Plus : Exp * Exp -> Exp
Times : Exp * Exp -> Exp
Uminus : Exp -> Exp
Int : IntConst -> Exp
: Var -> Exp
Var : Id -> Var
: String -> IntConst
: String -> Id
signature
constructors
Some : a -> Option(a)
None : Option(a)
signature
constructors
Cons : a * List(a) -> List(a)
Nil : List(a)
Conc : List(a) * List(a) -> List(a)
sdf2rtg -i m.def -o m.rtg -m M
.
sdf2rtg derives from an SDF syntax definition
m.def a regular tree grammar for the module
M and all modules it imports.
rtg2sig -i m.def -o m.rtg
.
rtg2sig generates from a regular tree grammar a
Stratego signature.
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
The GPP package is a tool suite for generic pretty-printing. GPP supports pretty-printing of parse-trees in the AsFix format with comment preservation and of abstract syntax trees. GPP supports the output formats plain text, LaTeX, and HTML. Formattings are defined in pretty print tables, which can be generated from SDF syntax definitions.
The Box language is used in the GPP framework as a language-independent intermediate representation. The input language dependent parts and the output format dependent parts of GPP are connected through this intermediate representation.
Box is a mark-up language to describe the intended layout of text
and is used in pretty print
tables. A Box expression is constructed by composing
sub-boxes using Box operators. These operators specify the
relative ordering of boxes. Examples of Box operators are the
H and V operator which
format boxes horizontally and vertically, respectively.
The exact formatting of each Box operator can be customized using
Box options. For example, to control the horizontal layout between
boxes the H operator supports the
hs space option.
For a detailed description of Box (including a description of all available Box operators) we refer to To Reuse Or To Be Reused (Chapter 4)
Pretty-print tables are used to specify how language constructs have to be pretty-printed. Pretty-print tables are used in combination with GPP front-ends, such ast2abox.
Pretty-print tables use Box as language to specify formatting of language constructs. A pretty-print table contains mappings from constructor names to Box expressions. For example, for the SDF production
Exp "+" Exp -> Exp {cons("Plus")}
A pretty-print entry looks like:
Plus -- H hs=1 [ _1 "+" _2]
Pretty-print tables are ordered such that pretty-print rules occuring first take preceedence over overlapping pretty-print rules defined later. The syntax of pretty-print tables is available in GPP.
Pretty-print tables can be generated from SDF syntax definitions using ppgen. Generated pretty-print rules can easiliy be customized by overruling them in additional pretty-print tables. The tool pptable-diff notifies inconsistensies in pretty-print tables after the syntax definition has changed and can be used to bring inconsistent table up-to-date.
To be able to specify formattings for all nested constructs that are allowed in SDF productions, so called selectors are used in pretty-print tables to refer to specific parts of an SDF production and to define a formatting for them. For example, the SDF prodcution
"return" Exp? ";" -> Stm {cons("Return")}
contains a nested symbol A?. To specify a formatting for this production, two pretty-print entries can be used:
Return -- H [ KW["return"] _1 ";" ] Return.1:opt -- H [ _1 ]
A selector consists of a constructor name followed by a list of number+type tuples. A number selects a particular subtree of a constructor application, the type denotes the type of the selected construct (sequence, optional, separated list etc.). This rather verbose selector mechanism allows unambiguous selection of subtrees. Its verbosity (by specifying both the number of a subtree and its type), makes pretty-print tables easier to understand and, more importantly, it enables pretty-printing of AST's, because with type information, a concrete term can be correctly recontructed from an AST. Pretty-print tables can thus be used for both formatting of parse-trees and AST's.
Below we summarize which selector types are available:
- opt
-
For SDF optionals
S? - iter
-
For non-empty SDF lists
S+ - iter-star
-
For possible empty SDF lists
S* - iter-sep
-
For SDF separator lists
{S1 S2}+. Observe that the symbolS1and the separatorS2are ordinary subtrees of the iter-sep construct which can be refered to as first and second subtree, respectively. - iter-star-sep
-
For SDF separator lists
{S1 S2}*. Its symbolS1and separatorS2can be refered to as first and second sub tree. - alt
-
For SDF alternatives
S1 | S2 | S3. According to the SDF syntax, alternatives are binary operators. The pretty-printer flattens all subsequent alternatives. Pretty-print rules can be specified for each alternative individually by specifying the number of each alternative. To be able to format literals in alternative, a special formatting rule can be defined for the construct (See the examples below). - seq
-
For SDF alternatives
(S1 S2 S3).
Below we list a simple SDF module with productions containing all above rule selectors.
module Symbols
exports
context-free syntax
A? -> S {cons("ex1")}
A+ -> S {cons("ex2")}
A* -> S {cons("ex3")}
{S1 S2}+ -> S {cons("ex4")}
{S1 S2}* -> S {cons("ex5")}
"one" | "two" | S? -> S {cons("ex6")}
("one" "two" S? ) -> S {cons("ex7")}
The following pretty-print table shows which pretty-print rules can be defined for this syntax:
[ ex1 -- _1, ex1.1:opt -- _1, ex2 -- _1, ex2.1:iter -- _1, ex3 -- _1, ex3.1:iter-star -- _1, ex4 -- _1, ex4.1:iter-sep -- _1 _2, ex5 -- _1, ex5.1:iter-star-sep -- _1 _2, ex6 -- _1, ex6.1:alt -- KW["one"] KW["two"] _1, ex6.1:alt.1:opt -- _1, ex7 -- _1, ex7.1:seq -- KW["one"] KW["two"] _1, ex7.1:seq.1:opt -- _1 ]
The pretty-print rule ex6.1:alt is a special
case. It contains three Box expressions, one for each
alternative. It is used to specify a formatting for the
non-nested literals "one" and
"two". During pretty-printing one of the three Box
expressions is selected, depending on alternative contained the
term to format.
In this section, we explain how you can generate a tool that restores all parentheses at the places where necessary according to the priorities and associativities of a language.
In this section, we explain how you can use Box in Stratego to implement a pretty-printer by hand.
After transformation, an abstract syntax tree should be turned into text again to be useful as a program. Mapping a tree into text can be seen as the inverse as parsing, and is thus called unparsing. When an unparser makes an attempt at producing human readable, instead of just compiler parsable, program text, an unparser is called a pretty-printer. We use the pretty-printing model as provided by the Generic Pretty-Printing package GPP. In this model a tree is unparsed to a Box expression, which contains text with markup for pretty-printing. A Box expression can be interpreted by different back-ends to produce text for different displaying devices, such as plain ASCII text, HTML, and LaTeX.
Unparsing is the inverse of parsing composed with abstract syntax tree composition. That is, an unparser turns an abstract syntax tree into a string, such that if the resulting string is parsed again, it produces the same abstract syntax tree.
An unparser can be organized in two phases. In the first phase,
each node in an abstract syntax tree is replaced with the concrete
syntax tree of the corresponding grammar production. In the
second phase, the strings at the leaves of the tree are
concatenated into a string. Figure 9.1
illustrates this process. The replacement of abstract syntax tree
nodes by concrete syntax patterns should be done according to the
productions of the syntax definition. An unparsing table is an
abstraction of a syntax definition definining the inverse mapping
from constructors to concrete syntax patterns. An entry c --
s1 ... sn defines a mapping for constructor c
to the sequence s1 ... sn, where each
s_i is either a literal string or a parameter
_i referring to the ith argument of the
constructor. Figure 9.2 shows an
unparsing table for some expression and statement
constructors. Applying an unparsing mapping to an abstract syntax
tree results in a tree structure with strings at the leafs, as
illustrated in Figure 9.1.
Figure 9.2. Unparsing table
[
Var -- _1,
Int -- _1,
Plus -- _1 "+" _2,
Minus -- _1 "-" _2,
Assign -- _1 ":=" _2,
Seq -- "(" _1 ")",
Seq.1:iter-star-sep -- _1 ";",
If -- "if" _1 "then" _2 "else" _3,
Call -- _1 "(" _2 ")",
Call.2:iter-star-sep -- _1 ","
]
Although the unparse of an abstract syntax tree is a text that can be parsed by a compiler, it is not necessarily a readable text. A pretty-printer is an unparser attempting to produce readable program text. A pretty-printer can be obtained by annotating the entries in an unparsing table with markup instructing a typesetting process. Figure 9.3 illustrates this process.
Box is a target independent formatting language, providing
combinators for declaring the two-dimensional positioning of boxes
of text. Typical combinators are H[b_1...b_n], which
combines the b_i boxes horizontally, and
V[b_1...b_n], which combines the
b_i boxes vertically. Figure 9.4 shows a pretty-print table with
Box markup. A more complete overview of the Box language and the
GPP tools can be found in Chapter 9.
Figure 9.4. Pretty-print table with Box markup
[
Var -- _1,
Int -- _1,
Plus -- H[_1 "+" _2],
Minus -- H[_1 "-" _2],
Assign -- H[_1 ":=" _2],
Seq -- H hs=0["(" V[_1] ")"],
Seq.1:iter-star-sep -- H hs=0[_1 ";"],
If -- V[V is=2[H["if" _1 "then"] _2]
V is=2["else" _3]],
Call -- H hs=0[_1 "(" H[_2] ")"],
Call.2:iter-star-sep -- H hs=0[_1 ","]
]
Figure 9.5. Pretty-printing of if-then-else statement
If(Eq(Var("n"),Int("1")),
Int("0"),
Times(Var("n"),
Call(Var("fac"),[Minus(Var("n"),Int("1"))])))


if n = 1 then 0 else n * fac(n - 1)
Note: correct pretty-printing of an abstract syntax tree requires
that it contains nodes representing parentheses in the right
places. Otherwise, reparsing a pretty-printed string might get a
different interpretation. The sdf2parenthesize
tool generates from an SDF definition a Stratego program that
places parentheses at the necessary places in the tree.
ppgen -i m.def -o m.pp
.
Ppgen generates from an SDF syntax definition a
pretty-print table with an entry for each context-free syntax
production with a constructor annotation. Typically it is
necessary to edit the pretty-print table to add appropriate Box
markup to the entries. The result should be saved under a
different name to avoid overwriting it.
ast2abox -p m.pp -i file.ast -o file.abox
.
ast2abox maps an abstract syntax tree
file.ast to an abstract syntax representation
file.abox of a Box term based on a pretty-print
table m.pp.
abox2text -i file.abox -o file.txt
.
abox2text formats a Box term as ASCII text.
pp-aterm -i file1.trm -o file2.trm
.
pp-aterm formats an ATerm as an ATerm in text
format, adding newlines and indentation to make the structure of
the term understandable. This is a useful tool to inspect terms
while debugging transformations.
term-to-dot -i file.trm -o file.dot (--tree | --graph)
.
Term-to-dot is another visualization tool for terms
that creates a dot graph representation, which can
be visualized using the dot tool from the graphviz
graph layout package. Term-to-dot can produce an
expanded tree view (--tree), or a directed acyclic
graph view (--graph) preserving the maximal sharing
in the term. This tool was used to produce the tree
visualizations in this chapter.
This tool is not part of the Stratego/XT distribution, but
included in the Stratego/XT Utilities package.
Stratego Version
This manual is being written for and with Stratego 0.16; You are advised to install the latest milestone for this release. See the download page at stratego-language.org
Program transformation is the mechanical manipulation of a program in order to improve it relative to some cost function C such that C(P) > C(tr(P)), i.e. the cost decreases as a result of applying the transformation. The cost of a program can be measured in different dimensions such as performance, memory usage, understandability, flexibility, maintainability, portability, correctness, or satisfaction of requirements. Related to these goals, program transformations are applied in different settings; e.g. compiler optimizations improve performance and refactoring tools aim at improving understandability. While transformations can be achieved by manual manipulation of programs, in general, the aim of program transformation is to increase programmer productivity by automating programming tasks, thus enabling programming at a higher-level of abstraction, and increasing maintainability and re-usability of programs. Automatic application of program transformations requires their implementation in a programming language. In order to make the implementation of transformations productive such a programming language should support abstractions for the domain of program transformation.
Stratego is a language designed for this purpose. It is a language based on the paradigm of rewriting with programmable rewriting strategies and dynamic rules.
Transformation by Rewriting.
Term rewriting is an attractive formalism for expressing basic
program transformations. A rewrite rule p1 -> p2
expresses that a program fragment matching the left-hand side
pattern p1 can be replaced by the instantiation of the right-hand
side pattern p2. For instance, the rewrite rule
|[ i + j ]| -> |[ k ]| where <add>(i, j) => k
expresses constant folding for addition, i.e. replacing an addition of two constants by their sum. Similarly, the rule
|[ if 0 then e1 else e2 ]| -> |[ e2 ]|
defines unreachable code elimination by reducing a conditional statement to its right branch since the left branch can never be executed. Thus, rewrite rules can directly express laws derived from the semantics of the programming language, making the verification of their correctness straightforward. A correct rule can be safely applied anywhere in a program. A set of rewrite rules can be directly operationalized by rewriting to normal form, i.e. exhaustive application of the rules to a term representing a program. If the rules are confluent and terminating, the order in which they are applied is irrelevant.
Limitations of Pure Rewriting. However, there are two limitations to the application of standard term rewriting techniques to program transformation: the need to intertwine rules and strategies in order to control the application of rewrite rules and the context-free nature of rewrite rules.
Transformation Strategies. Exhaustive application of all rules to the entire abstract syntax tree of a program is not adequate for most transformation problems. The system of rewrite rules expressing basic transformations is often non-confluent and/or non-terminating. An ad hoc solution that is often used is to encode control over the application of rules into the rules themselves by introducing additional function symbols. This intertwining of rules and strategies obscures the underlying program equalities, incurs a programming penalty in the form of rules that define a traversal through the abstract syntax tree, and disables the reuse of rules in different transformations.
Stratego solves the problem of control over the application of rules while maintaining the separation of rules and strategies. A strategy is a little program that makes a selection from the available rules and defines the order and position in the tree for applying the rules. Thus rules remain pure, are not intertwined with the strategy, and can be reused in multiple transformations. schemas.
Context-Senstive Transformation. The second problem of rewriting is the context-free nature of rewrite rules. A rule has access only to the term it is transforming. However, transformation problems are often context-sensitive. For example, when inlining a function at a call site, the call is replaced by the body of the function in which the actual parameters have been substituted for the formal parameters. This requires that the formal parameters and the body of the function are known at the call site, but these are only available higher-up in the syntax tree. There are many similar problems in program transformation, including bound variable renaming, typechecking, data flow transformations such as constant propagation, common-subexpression elimination, and dead code elimination. Although the basic transformations in all these applications can be expressed by means of rewrite rules, these require contextual information.
Outline. The following chapters give a tutorial for the Stratego language in which these ideas are explained and illustrated. The first three chapters outline the basic ideas of Stratego programming in bold strokes. Chapter 10 introduces the term notation used to represent source programs in Stratego. Chapter 11 shows how to set up, compile, and use a Stratego program. Chapter 12 introduces term rewrite rules and term rewriting. Chapter 13 argues the need for control over the application of rewrite rules and introduces strategies for achieving this.
The rest of the chapters in this tutorial explain the language in more detail. Chapter 14 examines the named rewrite rules, defines the notion of a rewriting strategy, and explains how to create reusable strategy expressions using definitions. Chapter 15 introduces combinators for the combination of simple transformations into more complex transformations. Chapter 16 re-examines the notion of a rule, and introduces the notions of building and matching terms, which provide the core to all manipulations of terms. It then goes on to show how these actions can be used to define higher-level constructs for expressing transformations, such as rewrite rules. Chapter 17 introduces the notion of data-type specific and generic traversal combinators. Chapter 18 shows how to generically define program analyses using type-unifying strategies. Chapter 19 shows ho to use the syntax of the source language in the patterns of transformation rules. Finally, Chapter 20 introduces the notion of dynamic rules for expressing context-sensitive transformations.
Table of Contents
- 10. Terms
- 11. Running Stratego Programs
- 12. Term Rewriting
- 13. Rewriting Strategies
- 14. Rules and Strategies
- 15. Strategy Combinators
- 16. Creating and Analyzing Terms
- 17. Traversal Strategies
- 18. Type Unifying Strategies
- 19. Concrete Object Syntax
- 20. Dynamic Rules
Table of Contents
Stratego programs transform terms. When using Stratego for program transformation terms typically represent the abstract syntax tree of a program. But Stratego does not much care what a term represents. Terms can just as well represent structured documents, software models, or anything else that can be rendered in a structured format. The chapters in Part II show how to transform a program text into a term by means of parsing, and to turn a term into program text again by means of pretty-printing. From now on we will just assume that we have terms that should be transformed and ignore parsing and pretty-printing.
Terms in Stratego are terms in the Annotated Term Format, or
ATerms for short. The ATerm format provides a set of constructs
for representing trees, comparable to XML or abstract data types
in functional programming languages.
For example, the code 4 + f(5 * x) might be
represented in a term as:
Plus(Int("4"), Call("f", [Mul(Int("5"), Var("x"))]))ATerms are constructed from the following elements:
- Integer
-
An integer constant, that is a list of decimal digits, is an ATerm. Examples:
1,12343. - String
-
A string constant, that is a list of characters between double quotes is an ATerm. Special characters such as double quotes and newlines should be escaped using a backslash. The backslash character itself should be escaped as well. Examples:
"foobar","string with quotes\"","escaped escape character\\ and a newline\n". - Constructor application
-
A constructor is an identifier, that is an alphanumeric string starting with a letter, or a double quoted string.
A constructor application
c(t1,...,tn)creates a term by applying a constructor to a list of zero or more terms. For example, the termPlus(Int("4"),Var("x"))uses the constructorsPlus,Int, andVarto create a nested term from the strings"4"and"x".When a constructor application has no subterms the parentheses may be omitted. Thus, the term
Zerois equivalent toZero(). Some people consider it good style to explicitly write the parentheses for nullary terms in Stratego programs. Through this rule, it is clear that a string is really a special case of a constructor application. - List
-
A list is a term of the form
[t1,...,tn], that is a list of zero or more terms between square brackets. While all applications of a specific constructor typically have the same number of subterms, lists can have a variable number of subterms. The elements of a list are typically of the same type, while the subterms of a constructor application can vary in type. Example: The second argument of the call to"f"in the termCall("f",[Int("5"),Var("x")])is a list of expressions. - Tuple
-
A tuple
(t1,...,tn)is a constructor application without constructor. Example:(Var("x"), Type("int")) - Annotation
-
The elements defined above are used to create the structural part of terms. Optionally, a term can be annotated with a list terms. These annotations typically carry additional semantic information about the term. An annotated term has the form
t{t1,...,tn}. Example:Lt(Var("n"),Int("1")){Type("bool")}. The contents of annotations is up to the application.
The term format described above is used in Stratego programs to denote terms, but is also used to exchange terms between programs. Thus, the internal format and the external format exactly coincide. Of course, internally a Stratego program uses a data-structure in memory with pointers rather than manipulating a textual representation of terms. But this is completely hidden from the Stratego programmer. There are a few facts that are useful to be aware of, though.
The internal representation used in Stratego programs maintains maximal sharing of subterms. This means that all occurrences of a subterm are represented by a pointer to the same node in memory. This makes comparing terms in Stratego for syntactic equality a very cheap operation, i.e., just a pointer comparison.
TODO: picture of tree vs dag representation
When writing a term to a file in order to exchange it with another tool there are several representations to choose from. The textual format described above is the canonical `meaning' of terms, but does not preserve maximal sharing. Therefore, there is also a Binary ATerm Format (BAF) that preserves sharing in terms. The program baffle can be used to convert between the textual and binary representations.
As a Stratego programmer you will be looking a lot at raw ATerms. Stratego pioneers would do this by opening an ATerm file in emacs and trying to get a sense of the structure by parenthesis highlighting and inserting newlines here and there. These days your life is much more pleasant through the tool pp-aterm, which adds layout to a term to make it readable. For example, parsing the following program
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n - 1))
in printint(fact(10))
end
produces the following ATerm (say in file fac.trm):
Let([FunDecs([FunDec("fact",[FArg("n",Tp(Tid("int")))],Tp(Tid("int")),
If(Lt(Var("n"),Int("1")),Int("1"),Seq([Times(Var("n"),Call(Var("fact"),
[Minus(Var("n"),Int("1"))]))])))])],[Call(Var("printint"),[Call(Var(
"fact"),[Int("10")])])])
By pretty-printing the term using pp-aterm as
$ pp-aterm -i fac.trm -o fac-pp.trm --max-term-size 20
we get a much more readable term:
Let(
[ FunDecs(
[ FunDec(
"fact"
, [FArg("n", Tp(Tid("int")))]
, Tp(Tid("int"))
, If(
Lt(Var("n"), Int("1"))
, Int("1")
, Seq([ Times(Var("n"), Call(Var("fact"), [Minus(Var("n"), Int("1"))]))
])
)
)
]
)
]
, [ Call(Var("printint"), [Call(Var("fact"), [Int("10")])])
]
)
To use terms in Stratego programs, their constructors should be
declared in a signature. A signature declares a number of
sorts and a number of constructors for
these sorts. For each constructor, a signature declares the
number and types of its arguments. For example, the following
signature declares some typical constructors for constructing
abstract syntax trees of expressions in a programming language:
signature
sorts Id Exp
constructors
: String -> Id
Var : Id -> Exp
Int : Int -> Exp
Plus : Exp * Exp -> Exp
Mul : Exp * Exp -> Exp
Call : Id * List(Exp) -> Exp
Currently, the Stratego compiler only checks the arity of constructor applications against the signature. Still, it is considered good style to also declare the types of constructors in a sensible manner for the purpose of documentation. Also, a later version of the language may introduce typechecking.
Table of Contents
Now let's see how we can actually transform terms using Stratego programs. In the rest of this chapter we will first look at the structure of Stratego programs, and how to compile and run them. In the next chapters we will then see how to define transformations.
The simplest program you can write in Stratego is the following
identity.str program:
module identity imports list-cons strategies main = id
It features the following elements:
Each Stratego file is a module, which has the
same name as the file it is stored in without the .str
extension.
A module may import other modules in order to
use the definitions in those modules.
A module may contain one or more strategies sections
that introduce new strategy definitions. It will become clear later
what strategies and strategy definitions are.
Each Stratego program has one main definition,
which indicates the strategy to be executed on invocation of the
program.
In the example, the body of this program's main definition is the
identity strategy id.
Now let's see what this program means. To find that out, we first
need to compile it, which we do using the Stratego compiler
strc as follows:
$ strc -i identity.str
[ strc | info ] Compiling 'identity.str'
[ strc | info ] Front-end succeeded : [user/system] = [0.59s/0.56s]
[ strc | info ] Back-end succeeded : [user/system] = [0.46s/0.16s]
[ strc | info ] C compilation succeeded : [user/system] = [0.28s/0.23s]
[ strc | info ] Compilation succeeded : [user/system] = [1.35s/0.95s]
The -i option of strc indicates the
module to compile. The compiler also reads all imported modules, in
this case the list-cons.str module that is part of the
Stratego library and that strc magically knows how to
find. The compiler prints some information about what it is doing,
i.e., the stages of compilation that it goes through and the times
for those stages. You can turn this off using the argument
--verbose 0. However, since the compiler is not very
fast, it may be satisfying to see something going on.
The result of compilation is an executable named
identity after the name of the main module of the
program. Just to satisfy our curiosity we inspect the file system
to see what the compiler has done:
$ ls -l identity*
-rwxrwxr-x 1 7182 Sep 7 14:54 identity*
-rw------- 1 1362 Sep 7 14:54 identity.c
-rw-rw-r-- 1 200 Sep 7 14:54 identity.dep
-rw-rw-r-- 1 2472 Sep 7 14:54 identity.o
-rw-rw-r-- 1 57 Sep 7 13:03 identity.str
Here we see that in addition to the executable the compiler has
produced a couple of other files. First of all the
identity.c file gives away the fact that the compiler
first translates a Stratego program to C and then uses the C
compiler to compile to machine code. The identity.o
file is the result of compiling the generated C program. Finally,
the contents of the identity.dep file will look
somewhat like this:
identity: \
/usr/local/share/stratego-lib/collection/list/cons.rtree \
/usr/local/share/stratego-lib/list-cons.rtree \
./identity.str
It is a rule in the Make language that declares the dependencies of
the identity program. You can include this file in a
Makefile to automate its compilation. For example, the
following Makefile automates the compilation of the
identity program:
include identity.dep
identity : identity.str
strc -i identity.str
Just invoke make on the command-line whenever you
change something in the program.
Ok, we were digressing a bit. Let's turn back to finding out what
the identity program does. When we execute the program
with some arbitrary arguments on the command-line, this is what
happens:
$ ./identity foo bar
["./identity","foo","bar"]
The program writes to stdout the list of command-line
arguments as a list of strings in the ATerm format.
So what we have learned is that a Stratego program applies its
main strategy to the list of command-line arguments, and writes
the resulting term to stdout. Since the strategy in
the identity program is the identity transformation
it just writes the original command-line arguments (as a term).
That was instructive, but not very useful. We are not interested
in transforming lists of strings, but rather programs represented
as terms. So we want to read a term from a file, transform it, and
write it to another file. Let's open the bag of tricks. The
identity-io program improves the previous program:
module identity-io imports libstrategolib strategies main = io-wrap(id)
The program looks similar to the previous one, but there are a
couple of differences. First, instead of importing module
list-cons, this module imports
libstrategolib, which is the interface to the
separately compiled Stratego library. This library provides a host
of useful strategies that are needed in implementing program
transformations. Part IV gives an
overview of the Stratego library, and we will every now and then
use some useful strategies from the library before we get there.
Right now we are interested in the io-wrap strategy
used above. It implements a wrapper strategy that takes care of
input and output for our program. To compile the program we need
to link it with the stratego-lib library using the
-la option:
$ strc -i identity-io.str -la stratego-lib
What the relation is between libstrategolib and
stratego-lib will become clear later; knowing that it
is needed to compile programs using libstrategolib suffices
for now.
If we run the compiled identity-io program with its
--help option we see the standard interface supported
by the io-wrap strategy:
$ ./identity-io --help
Options:
-i f|--input f Read input from f
-o f|--output f Write output to f
-b Write binary output
-S|--silent Silent execution (same as --verbose 0)
--verbose i Verbosity level i (default 1)
( i as a number or as a verbosity descriptor:
emergency, alert, critical, error,
warning, notice, info, debug, vomit )
-k i | --keep i Keep intermediates (default 0)
--statistics i Print statistics (default 0 = none)
-h|-?|--help Display usage information
--about Display information about this program
--version Same as --about
The most relevant options are the -i option for the
input file and the -o option for the output file. For
instance, if we have some file foo-bar.trm containing
an ATerm we can apply the program to it:
$echo "Foo(Bar())" > foo-bar.trm$./identity-io -i foo-bar.trm -o foo-bar2.trm$cat foo-bar2.trm Foo(Bar)
If we leave out the -i and/or -o options,
input is read from stdin and output is written to
stdout. Thus, we can also invoke the program in a
pipe:
$ echo "Foo(Bar())" | ./identity-io
Foo(Bar)
Now it might seem that the identity-io program just
copies its input file to the output file. In fact, the
identity-io does not just accept any input. If we try
to apply the program to a text file that is not an ATerm, it
protests and fails:
$ echo "+ foo bar" | ./identity-io
readFromTextFile: parse error at line 0, col 0
not a valid term
./identity: rewriting failed
So we have written a program to check if a file represents an ATerm.
A Stratego program based on io-wrap defines a
transformation from terms to terms. Such transformations can be
combined into more complex transformations, by creating a chain of
tool invocations.
For example, if we have a Stratego program trafo-a
applying some undefined transformation-a to the input
term of the program
module trafo-a imports libstrategolib strategies main = io-wrap(transformation-a) transformation-a = ...
and we have another similar program trafo-b applying a
transformation-b
module tool-b imports libstrategolib strategies main = io-wrap(transformation-b) transformation-b = ...
then we can combine the transformations to transform an
input file to an output file using a Unix
pipe, as in
$ tool-a -i input | tool-b -o output
or using an intermediate file:
$tool-a -i input -o intermediate$tool-b -i intermediate -o output
We have just learned how to write, compile, and execute Stratego programs. This is the normal mode for development of transformation systems with Stratego. Indeed, we usually do not invoke the compiler from the command-line `by hand', but have an automated build system based on (auto)make to build all programs in a project at once. For learning to use the language this can be rather laborious, however. Therefore, we have also developed the Stratego Shell, an interactive interpreter for the Stratego language. The shell allows you to type in transformation strategies on the command-line and directly seeing their effect on the current term. While this does not scale to developing large programs, it can be instructive to experiment while learning the language. In the following chapters we will use the stratego-shell to illustrate various features of the language.
Here is a short session with the Stratego Shell that shows the basics of using it:
$stratego-shellstratego>:show ()stratego>!Foo(Bar()) Foo(Bar)stratego>id Foo(Bar)stratego>fail command failedstratego>:show Foo(Bar)stratego>:quit Foo(Bar)$
The shell is invoked by calling the command
stratego-shell on the regular command-line. The
stratego> prompt then indicates that you have entered
the Stratego Shell. After the prompt you can enter strategies or
special shell commands.
Strategies are the statements and functions of the Stratego
language. A strategy transforms a term into a new term, or
fails. The term to which a strategy is applied, is called the
current term. In the Stratego Shell you can see
the current term with :show. In the session above
we see that the current term is the empty tuple if you have just
started the Stratego Shell.
At the prompt of the shell you can enter strategies. If the strategy
succeeds, then the shell will show the transformed term, which is
now the new current term.
For example, in the session above the strategy
!Foo(Bar()) replaces the current term with the term
Foo(Bar()), which is echoed directly after applying the
strategy. The next strategy that is applied is the identity strategy
id that we saw before. Here it becomes clear that it
just returns the term to which it is applied.
Thus, we have the following general scheme of applying a strategy to
the current term:
current termstratego>strategy expressiontransformed currentstratego>
Strategies can also fail. For example, the application of the
fail strategy always fails. In the case of failure, the
shell will print a message and leave the current term untouched:
current termstratego>strategy expressioncommand failedstratego>:showcurrent term
Finally, you can leave the shell using the :quit command.
The Stratego Shell has a number of non-strategy commands to operate
the shell configuration. Theses commands are recognizable by the
: prefix. The :help command tells you
what commands are available in the shell:
$stratego-shellstratego>:help Rewriting strategy rewrite the current subject term with strategy Defining Strategies id = strategy define a strategy (doesn't change the current subject term) id : rule define a rule (doesn't change the current subject term) import modname import strategy definitions from 'modname' (file system or xtc) :undef id delete defintions of all strategies 'id'/(s,t) :undef id(s,t) delete defintion of strategy 'id'/(s,t) :reset delete all term bindings, all strategies, reset syntax. Debugging :show show the current subject term :autoshow on|off show the current subject term after each rewrite :binding id show term binding of id :bindings show all term bindings :showdef id show defintions of all strategies 'id'/(s,t) :showdef id(s,t) show defintion of strategy 'id'/(s,t) :showast id(s,t) show ast of defintion of strategy 'id'/(s,t) Concrete Syntax :syntax defname set the syntax to the sdf definition in 'defname'. XTC :xtc import pathname Misc :include file execute command in the script of `file` :verbose int set the verbosity level (0-9) :clear clear the screen :exit exit the Stratego Shell :quit same as :exit :q same as :exit :about information about the Stratego Shell :help show this help information stratego>
Let's summarize what we have learned so far about Stratego programming.
First, a Stratego program is divided into
modules, which reside in files with extension
.str and have the following general form:
module mod0
imports libstrategolib mod1 mod2
signature
sorts A B C
constructors
Foo : A -> B
Bar : A
strategies
main = io-wrap(foo)
foo = id
Modules can import other modules and can define signatures for
declaring the structure of terms and can define strategies, which we
not really know much about yet.
However, the io-wrap strategy can be used to handle the
input and output of a Stratego program. This strategy is defined in
the libstrategolib module, which provides an interface to the
Stratego Library.
The main module of a Stratego program should have a
main strategy that defines the entry point of the
program.
Next, a Stratego program is compiled to an executable program using
the Stratego Compiler strc.
$ strc -i mod0 -la stratego-lib
The resulting executable applies the main strategy to
command-line arguments turned into a list-of-strings term.
The io-wrap strategy interprets these command-line
arguments to handle input and output using standard command-line
options.
Finally, the Stratego Shell can be used to invoke strategies interactively.
$stratego-shellstratego>id ()stratego>
Next up: transforming terms with rewrite rules.
Table of Contents
In Part II we saw how terms provide a structured representation for programs derived from a formal definition of the syntax of a programming language. Transforming programs then requires tranformation of terms. In this chapter we show how to implement term transformations using term rewriting in Stratego. In term rewriting a term is transformed by repeated application of rewrite rules.
To see how this works we take as example the language of propositional formulae, also known as Boolean expressions:
module prop
signature
sorts Prop
constructors
False : Prop
True : Prop
Atom : String -> Prop
Not : Prop -> Prop
And : Prop * Prop -> Prop
Or : Prop * Prop -> Prop
Impl : Prop * Prop -> Prop
Eq : Prop * Prop -> Prop
Given this signature we can write terms such as
And(Impl(True,False),False), and
And(Atom("p"),False)). Atoms are also known as
proposition letters; they are the variables in propositional
formulae. That is, the truth value of an atom should be provided in
order to fully evaluate an expression. Here we will evaluate
expressions as far as possible, a transformation also known as
constant folding. We will do this using
rewrite rules that define how to simplify a
single operator application.
A term pattern is a term with meta
variables, which are identifiers that are not declared
as (nullary) constructors. For example, And(x, True)
is a term pattern with variable x. Variables in term
patterns are sometimes called meta variables,
to distinguish them from variables in the source language being
processed. For example, while atoms in the proposition expressions
are variables from the point of view of the language, they are not
variables from the perspective of a Stratego program.
A term pattern p matches with a
term t, if there is a
substitution that replaces the variables in
p such that it becomes equal to t. For
example, the pattern And(x, True) matches the term
And(Impl(True,Atom("p")),True) because replacing the
variable x in the pattern by
Impl(True,Atom("p")) makes the pattern equal to the
term. Note that And(Atom("x"),True) does
not match the term
And(Impl(True,Atom("p")),True), since the subterms
Atom("x") and Impl(True,Atom("p")) do not
match.
An unconditional rewrite rule has the form
L : p1 -> p2, where L is the name of the
rule, p1 is the left-hand side and p2 the
right-hand side term pattern.
A rewrite rule L : p1 -> p2 applies to a term
t when the pattern p1 matches
t. The result is the instantiation of p2
with the variable bindings found during matching.
For example, the rewrite rule
E : Eq(x, False) -> Not(x)
rewrites the term Eq(Atom("q"),False) to
Not(Atom("q")), since the variable x is
bound to the subterm Atom("q").
Now we can create similar evaluation rules for all constructors of
sort Prop:
module prop-eval-rules imports prop rules E : Not(True) -> False E : Not(False) -> True E : And(True, x) -> x E : And(x, True) -> x E : And(False, x) -> False E : And(x, False) -> False E : Or(True, x) -> True E : Or(x, True) -> True E : Or(False, x) -> x E : Or(x, False) -> x E : Impl(True, x) -> x E : Impl(x, True) -> True E : Impl(False, x) -> True E : Eq(False, x) -> Not(x) E : Eq(x, False) -> Not(x) E : Eq(True, x) -> x E : Eq(x, True) -> x
Note that all rules have the same name, which is allowed in Stratego.
Next we want to normalize terms with respect to a collection of rewrite rules. This entails applying all rules to all subterms until no more rules can be applied. The following module defines a rewrite system based on the rules for propositions above:
module prop-eval imports libstrategolib prop-eval-rules strategies main = io-wrap(eval) eval = innermost(E)
The module imports the Stratego Library
(libstrategolib) and the module with the evaluation
rules, and then defines the main strategy to apply
innermost(E) to the input term. (See the discussion of
io-wrap in Section 11.2.)
The innermost strategy from the library exhaustively
applies its argument transformation to the term it is applied to,
starting with `inner' subterms.
We can now compile the program as discussed in Chapter 11:
$ strc -i prop-eval.str -la stratego-lib
This results in an executable prop-eval that can be
used to evaluate Boolean expressions. For example, here are some
applications of the program:
$cat test1.prop And(Impl(True,And(False,True)),True)$./prop-eval -i test1.prop False$cat test2.prop And(Impl(True,And(Atom("p"),Atom("q"))),ATom("p"))$./prop-eval -i test2.prop And(And(Atom("p"),Atom("q")),ATom("p"))
We can also import these definitions in the Stratego Shell, as illustrated by the following session:
$stratego-shellstratego>import prop-evalstratego>!And(Impl(True(),And(False(),True())),True()) And(Impl(True,And(False,True)),True)stratego>eval Falsestratego>!And(Impl(True(),And(Atom("p"),Atom("q"))),ATom("p")) And(Impl(True,And(Atom("p"),Atom("q"))),ATom("p"))stratego>eval And(And(Atom("p"),Atom("q")),ATom("p"))stratego>:quit And(And(Atom("p"),Atom("q")),ATom("p"))$
The first command imports the prop-eval module, which
recursively loads the evaluation rules and the library, thus making
its definitions available in the shell. The ! commands
replace the current term with a new term. (This
build strategy will be properly introduced in
Chapter 16.)
The next commands apply the eval strategy to various
terms.
Next we extend the rewrite rules above to rewrite a Boolean expression to disjunctive normal form. A Boolean expression is in disjunctive normal form if it conforms to the following signature:
signature
sorts Or And NAtom Atom
constructors
Or : Or * Or -> Or
: And -> Or
And : And * And -> And
: NAtom -> And
Not : Atom -> NAtom
: Atom -> NAtom
Atom : String -> Atom
We use this signature only to describe what a disjunctive normal
form is, not in an the actual Stratego program. This is not
necessary, since terms conforming to the DNF signature are also
Prop terms as defined before.
For example, the disjunctive normal form of
And(Impl(Atom("r"),And(Atom("p"),Atom("q"))),ATom("p"))
is
Or(And(Not(Atom("r")),ATom("p")),
And(And(Atom("p"),Atom("q")),ATom("p")))
Module prop-dnf-rules extends the rules defined in
prop-eval-rules with rules to achieve disjunctive
normal forms:
module prop-dnf-rules imports prop-eval-rules rules E : Impl(x, y) -> Or(Not(x), y) E : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) E : Not(Not(x)) -> x E : Not(And(x, y)) -> Or(Not(x), Not(y)) E : Not(Or(x, y)) -> And(Not(x), Not(y)) E : And(Or(x, y), z) -> Or(And(x, z), And(y, z)) E : And(z, Or(x, y)) -> Or(And(z, x), And(z, y))
The first two rules rewrite implication (Impl) and
equivalence (Eq) to combinations of And,
Or, and Not.
The third rule removes double negation.
The fifth and sixth rules implement the well known DeMorgan laws.
The last two rules define distribution of conjunction over
disjunction.
We turn this set of rewrite rules into a compilable Stratego program in the same way as before:
module prop-dnf imports libstrategolib prop-dnf-rules strategies main = io-wrap(dnf) dnf = innermost(E)
compile it in the usual way
$ strc -i prop-dnf.str -la stratego-lib
so that we can use it to transform terms:
$cat test3.prop And(Impl(Atom("r"),And(Atom("p"),Atom("q"))),ATom("p"))$./prop-dnf -i test3.prop Or(And(Not(Atom("r")),ATom("p")),And(And(Atom("p"),Atom("q")),ATom("p")))
We have seen how to define simple transformations on terms using
unconditional term rewrite rules. Using the innermost
strategy, rules are applied exhaustively to all subterms of the
subject term.
The implementation of a rewrite system in Stratego has the following
form:
module mod
imports libstrategolib
signature
sorts A B C
constructors
Foo : A * B -> C
rules
R : p1 -> p2
R : p3 -> p4
strategies
main = io-wrap(rewr)
rewr = innermost(R)
The ingredients of such a program can be divided over several modules. Thus, a set of rules can be used in multiple rewrite systems.
Compiling the module by means of the command
$ strc -i mod.str -la stratego-lib
produces an executable mod that can be used to
transform terms.
Table of Contents
In Chapter 12 we saw how term
rewriting can be used to implement transformations on programs
represented by means of terms.
Term rewriting involves exhaustively applying rules to subterms
until no more rules apply.
This requires a strategy for selecting the
order in which subterms are rewritten.
The innermost strategy introduced in Chapter 12 applies rules automatically throughout a
term from inner to outer terms, starting with the leaves.
The nice thing about term rewriting is that there is no need to
define traversals over the syntax tree; the rules express basic
transformation steps and the strategy takes care of applying it
everywhere.
However, the complete normalization approach of rewriting turns out
not to be adequate for program transformation, because rewrite
systems for programming languages will often be non-terminating
and/or non-confluent.
In general, it is not desirable to apply all rules at the same time
or to apply all rules under all circumstances.
Consider for example, the following extension of
prop-dnf-rules with distribution rules to achieve
conjunctive normal forms:
module prop-cnf imports prop-dnf-rules rules E : Or(And(x, y), z) -> And(Or(x, z), Or(y, z)) E : Or(z, And(x, y)) -> And(Or(z, x), Or(z, y)) strategies main = io-wrap(cnf) cnf = innermost(E)
This rewrite system is non-terminating because after applying one of the and-over-or distribution rules, the or-over-and distribution rules introduced here can be applied, and vice versa.
And(Or(Atom("p"),Atom("q")), Atom("r"))
->
Or(And(Atom("p"), Atom("r")), And(Atom("q"), Atom("r")))
->
And(Or(Atom("p"), And(Atom("q"), Atom("r"))),
Or(Atom("r"), And(Atom("q"), Atom("r"))))
->
...
There are a number of solutions to this problem. We'll first discuss a couple of solutions within pure rewriting, and then show how programmable rewriting strategies can overcome the problems of these solutions.
The non-termination of prop-cnf is due to the fact that
the and-over-or and or-over-and distribution rules interfere with
each other.
This can be prevented by refactoring the module structure such that
the two sets of rules are not present in the same rewrite system.
For example, we could split module prop-dnf-rules into
prop-simplify and prop-dnf2 as follows:
module prop-simplify imports prop-eval-rules rules E : Impl(x, y) -> Or(Not(x), y) E : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) E : Not(Not(x)) -> x E : Not(And(x, y)) -> Or(Not(x), Not(y)) E : Not(Or(x, y)) -> And(Not(x), Not(y))
module prop-dnf2 imports prop-simplify rules E : And(Or(x, y), z) -> Or(And(x, z), And(y, z)) E : And(z, Or(x, y)) -> Or(And(z, x), And(z, y)) strategies main = io-wrap(dnf) dnf = innermost(E)
Now we can reuse the rules from prop-simplify without
the and-over-or distribution rules to create a
prop-cnf2 for normalizing to conjunctive normal form:
module prop-cnf2 imports prop-simplify rules E : Or(And(x, y), z) -> And(Or(x, z), Or(y, z)) E : Or(z, And(x, y)) -> And(Or(z, x), Or(z, y)) strategies main = io-wrap(cnf) cnf = innermost(E)
Although this solves the non-termination problem, it is not an ideal solution. In the first place it is not possible to apply the two transformations in the same program. In the second place, extrapolating the approach to fine-grained selection of rules might require definition of a single rule per module.
Another common solution to this kind of problem is to introduce
additional constructors that achieve normalization under a
restricted set of rules. That is, the original set of rules p1
-> p2 is transformed into rules of the form f(p_1) ->
p_2', where f is some new constructor symbol and
the right-hand side of the rule also contains such new
constructors. In this style of programming, constructors such as
f are called functions and are
distinghuished from constructors. Normal forms over such rewrite
systems are assumed to be free of these `function' symbols;
otherwise the function would have an incomplete definition.
To illustrate the approach we adapt the DNF rules by introducing the
function symbols Dnf and DnfR. (We ignore
the evaluation rules in this example.)
module prop-dnf3
imports libstrategolib prop
signature
constructors
Dnf : Prop -> Prop
DnfR : Prop -> Prop
rules
E : Dnf(Atom(x)) -> Atom(x)
E : Dnf(Not(x)) -> DnfR(Not(Dnf(x)))
E : Dnf(And(x, y)) -> DnfR(And(Dnf(x), Dnf(y)))
E : Dnf(Or(x, y)) -> Or(Dnf(x), Dnf(y))
E : Dnf(Impl(x, y)) -> Dnf(Or(Not(x), y))
E : Dnf(Eq(x, y)) -> Dnf(And(Impl(x, y), Impl(y, x)))
E : DnfR(Not(Not(x))) -> x
E : DnfR(Not(And(x, y))) -> Or(Dnf(Not(x)), Dnf(Not(y)))
E : DnfR(Not(Or(x, y))) -> Dnf(And(Not(x), Not(y)))
D : DnfR(Not(x)) -> Not(x)
E : DnfR(And(Or(x, y), z)) -> Or(Dnf(And(x, z)), Dnf(And(y, z)))
E : DnfR(And(z, Or(x, y))) -> Or(Dnf(And(z, x)), Dnf(And(z, y)))
D : DnfR(And(x, y)) -> And(x, y)
strategies
main = io-wrap(dnf)
dnf = innermost(E <+ D)
The Dnf function mimics the innermost normalization
strategy by recursively traversing terms.
The auxiliary transformation function DnfR is used to
encode the distribution and negation rules.
The D rules are default rules that
are only applied if none of the E rules apply, as
specified by the strategy expression E <+ D.
In order to compute the disjunctive normal form of a term, we have
to `apply' the Dnf function to it, as illustrated in
the following application of the prop-dnf3 program:
$cat test1.dnf Dnf(And(Impl(Atom("r"),And(Atom("p"),Atom("q"))),ATom("p")))$./prop-dnf3 -i test1.dnf Or(And(Not(Atom("r")),Dnf(Dnf(ATom("p")))), And(And(Atom("p"),Atom("q")),Dnf(Dnf(ATom("p")))))
For conjunctive normal form we can create a similar definition, which can now co-exist with the definition of DNF. Indeed, we could then simultaneously rewrite one subterm to DNF and the other to CNF.
E : DC(x) -> (Dnf(x), Cnf(x))
In the solution above, the original rules have been completely
intertwined with the Dnf transformation.
The rules for negation cannot be reused in the definition of
normalization to conjunctive normal form.
For each new transformation a new traversal function and new
transformation functions have to be defined.
Many additional rules had to be added to traverse the term to find
the places to apply the rules.
In the modular solution we had 5 basic rules and 2 additional rules
for DNF and 2 rules for CNF, 9 in total. In the functionalized
version we needed 13 rules for each
transformation, that is 26 rules in total.
In general, there are two problems with the functional approach to encoding the control over the application of rewrite rules, when comparing it to the original term rewriting approach: traversal overhead and loss of separation of rules and strategies.
In the first place, the functional encoding incurs a large overhead due to the explicit specification of traversal. In pure term rewriting, the strategy takes care of traversing the term in search of subterms to rewrite. In the functional approach traversal is spelled out in the definition of the function, requiring the specification of many additional rules. A traversal rule needs to be defined for each constructor in the signature and for each transformation. The overhead for transformation systems for real languages can be inferred from the number of constructors for some typical languages:
language : constructors Tiger : 65 C : 140 Java : 140 COBOL : 300 - 1200
In the second place, rewrite rules and the strategy that defines their application are completely intertwined. Another advantage of pure term rewriting is the separation of the specification of the rules and the strategy that controls their application. Intertwining these specifications makes it more difficult to understand the specification, since rules cannot be distinghuished from the transformation they are part of. Furthermore, intertwining makes it impossible to reuse the rules in a different transformation.
Stratego introduced the paradigm of programmable rewriting strategies with generic traversals, a unifying solution in which application of rules can be carefully controlled, while incurring minimal traversal overhead and preserving separation of rules and strategies.
The following are the design criteria for strategies in Stratego:
- Separation of rules and strategy
-
Basic transformation rules can be defined separately from the strategy that applies them, such that they can be understood independently.
- Rule selection
-
A transformation can select the necessary set of rules from a collection (library) of rules.
- Control
-
A transformation can exercise complete control over the application of rules. This control may be fine-grained or course-grained depending on the application.
- No traversal overhead
-
Transformations can be defined without overhead for the definition of traversals.
- Reuse of rules
-
Rules can be reused in different transformations.
- Reuse of traversal schemas
-
Traversal schemas can be defined generically and reused in different transformations.
In the next chapters we will examine the language constructs that Stratego provides for programming with strategies, starting with the low-level actions of building and matching terms. To get a feeling for the purpose of these constructs, we first look at a couple of typical idioms of strategic rewriting.
The basic idiom of program transformation achieved with term rewriting is that of cascading transformations. Instead of applying a single complex transformation algorithm to a program, a number of small, independent transformations are applied in combination throughout a program or program unit to achieve the desired effect. Although each individual transformation step achieves little, the cumulative effect can be significant, since each transformation feeds on the results of the ones that came before it.
One common cascading of transformations is accomplished by
exhaustively applying rewrite rules to a subject term. In Stratego
the definition of a cascading normalization strategy with respect to
rules R1, ... ,Rn can be formalized using
the innermost strategy that we saw before:
simplify = innermost(R1 <+ ... <+ Rn)
The argument strategy of innermost is a
selection of rules. By giving
different names to rules, we can control the
selection used in each transformation. There can be multiple
applications of innermost to different sets of rules,
such that different transformations can co-exist in the same module
without interference. Thus, it is now possible to develop a large
library of transformation rules that can be called upon when
necessary, without having to compose a rewrite system by cutting and
pasting.
For example, the following module defines the normalization of
proposition formulae to both disjunctive and to conjunctive normal
form:
module prop-laws imports libstrategolib prop rules DefI : Impl(x, y) -> Or(Not(x), y) DefE : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) DN : Not(Not(x)) -> x DMA : Not(And(x, y)) -> Or(Not(x), Not(y)) DMO : Not(Or(x, y)) -> And(Not(x), Not(y)) DAOL : And(Or(x, y), z) -> Or(And(x, z), And(y, z)) DAOR : And(z, Or(x, y)) -> Or(And(z, x), And(z, y)) DOAL : Or(And(x, y), z) -> And(Or(x, z), Or(y, z)) DOAR : Or(z, And(x, y)) -> And(Or(z, x), Or(z, y)) strategies dnf = innermost(DefI <+ DefE <+ DAOL <+ DAOR <+ DN <+ DMA <+ DMO) cnf = innermost(DefI <+ DefE <+ DOAL <+ DOAR <+ DN <+ DMA <+ DMO) main-dnf = io-wrap(dnf) main-cnf = io-wrap(cnf)
The rules are named, and for each strategy different selections from the ruleset are made.
The module even defines two main strategies, which allows us to use
one module for deriving multiple programs. Using the
--main option of strc we declare
which strategy to invoke as main strategy in a particular
program. Using the -o option we can give a different
name to each derived program.
$ strc -i prop-laws.str -la stratego-lib --main main-dnf -o prop-dnf4
Cascading transformations can be defined with other strategies as
well, and these strategies need not be exhaustive, but can be
simpler one-pass traversals.
For example, constant folding of Boolean expressions only requires a
simple one-pass bottom-up traversal. This can be achieved using the
bottomup strategy according the the following scheme:
simplify = bottomup(repeat(R1 <+ ... <+ Rn))
The bottomup strategy applies its argument strategy to
each subterm in a bottom-to-top traversal. The repeat
strategy applies its argument strategy repeatedly to a term.
Module prop-eval2 defines the evaluation rules for
Boolean expressions and a strategy for applying them using this
approach:
module prop-eval2 imports libstrategolib prop rules Eval : Not(True) -> False Eval : Not(False) -> True Eval : And(True, x) -> x Eval : And(x, True) -> x Eval : And(False, x) -> False Eval : And(x, False) -> False Eval : Or(True, x) -> True Eval : Or(x, True) -> True Eval : Or(False, x) -> x Eval : Or(x, False) -> x Eval : Impl(True, x) -> x Eval : Impl(x, True) -> True Eval : Impl(False, x) -> True Eval : Eq(False, x) -> Not(x) Eval : Eq(x, False) -> Not(x) Eval : Eq(True, x) -> x Eval : Eq(x, True) -> x strategies main = io-wrap(eval) eval = bottomup(repeat(Eval))
The strategy eval applies these rules in a bottom-up
traversal over a term, using the bottomup(s)
strategy. At each sub-term, the rules are applied repeatedly until
no more rule applies using the repeat(s) strategy. This
is sufficient for the Eval rules, since the rules never
construct a term with subterms that can be rewritten.
Another typical example of the use of one-pass traversals is desugaring, that is rewriting language constructs to more basic language constructs. Simple desugarings can usually be expressed using a single top-to-bottom traversal according to the scheme
simplify = topdown(try(R1 <+ ... <+ Rn))
The topdown strategy applies its argument strategy to
a term and then traverses the resulting term.
The try strategy tries to apply its argument strategy
once to a term.
Module prop-desugar defines a number of desugaring
rules for Boolean expressions, defining propositional operators in
terms of others. For example, rule DefN defines
Not in terms of Impl, and rule
DefI defines Impl in terms of
Or and Not. So not all rules should be
applied in the same transformation or non-termination would result.
module prop-desugar
imports prop libstrategolib
rules
DefN : Not(x) -> Impl(x, False)
DefI : Impl(x, y) -> Or(Not(x), y)
DefE : Eq(x, y) -> And(Impl(x, y), Impl(y, x))
DefO1 : Or(x, y) -> Impl(Not(x), y)
DefO2 : Or(x, y) -> Not(And(Not(x), Not(y)))
DefA1 : And(x, y) -> Not(Or(Not(x), Not(y)))
DefA2 : And(x, y) -> Not(Impl(x, Not(y)))
IDefI : Or(Not(x), y) -> Impl(x, y)
IDefE : And(Impl(x, y), Impl(y, x)) -> Eq(x, y)
strategies
desugar =
topdown(try(DefI <+ DefE))
impl-nf =
topdown(repeat(DefN <+ DefA2 <+ DefO1 <+ DefE))
main-desugar =
io-wrap(desugar)
main-inf =
io-wrap(impl-nf)
The strategies desugar and impl-nf define
two different desugaring transformation based on these rules.
The desugar strategy gets rid of the implication and
equivalence operators, while the impl-nf strategy
reduces an expression to implicative normal-form, a format in which
only implication (Impl) and
False are used.
A final example of a one-pass traversal is the downup
strategy, which applies its argument transformation during a
traversal on the way down, and again on the way up:
simplify = downup(repeat(R1 <+ ... <+ Rn))
An application of this strategy is a more efficient implementation of constant folding for Boolean expressions:
eval = downup(repeat(Eval))
This strategy reduces terms such as
And(... big expression ..., False)
in one step (to False in this case), while the
bottomup strategy defined above would first evaluate
the big expression.
Cascading transformations apply a number of rules one after another to an entire tree. But in some cases this is not appropriate. For instance, two transformations may be inverses of one another, so that repeatedly applying one and then the other would lead to non-termination. To remedy this difficulty, Stratego supports the idiom of staged transformation.
In staged computation, transformations are not applied to a subject term all at once, but rather in stages. In each stage, only rules from some particular subset of the entire set of available rules are applied. In the TAMPR program transformation system this idiom is called sequence of normal forms, since a program tree is transformed in a sequence of steps, each of which performs a normalization with respect to a specified set of rules. In Stratego this idiom can be expressed directly according to the following scheme:
strategies
simplify =
innermost(A1 <+ ... <+ Ak)
; innermost(B1 <+ ... <+ Bl)
; ...
; innermost(C1 <+ ... <+ Cm)
In conventional program optimization, transformations are applied throughout a program. In optimizing imperative programs, for example, complex transformations are applied to entire programs. In GHC-style compilation-by-transformation, small transformation steps are applied throughout programs. Another style of transformation is a mixture of these ideas. Instead of applying a complex transformation algorithm to a program we use staged, cascading transformations to accumulate small transformation steps for large effect. However, instead of applying transformations throughout the subject program, we often wish to apply them locally, i.e., only to selected parts of the subject program. This allows us to use transformations rules that would not be beneficial if applied everywhere.
One example of a strategy which achieves such a transformation is
strategies
transformation =
alltd(
trigger-transformation
; innermost(A1 <+ ... <+ An)
)
The strategy alltd(s) descends into a term until a
subterm is encountered for which the transformation s
succeeds. In this case the strategy
trigger-transformation recognizes a program fragment
that should be transformed. Thus, cascading transformations are
applied locally to terms for which the transformation is
triggered. Of course more sophisticated strategies can be used for
finding application locations, as well as for applying the rules
locally. Nevertheless, the key observation underlying this idiom
remains: Because the transformations to be applied are local,
special knowledge about the subject program at the point of
application can be used. This allows the application of rules that
would not be otherwise applicable.
While term rewrite rules can express individual transformation steps, the exhaustive applications of all rules to all subterms is not always desirable. The selection of rules to apply through the module system does not allow transformations to co-exist and may require very small-grained modules. The `functionalization' of rewrite rules leads to overhead in the form of traversal definitions and to the loss of separation between rules and strategy. The paradigm of rewriting with programmable strategies allows the separate definition of individual rewrite rules, which can be (re)used in different combinations with a choice of strategies to form a variety of transformations. Idioms such as cascading transformations, one-pass traversals, staged, and local transformations cater for different styles of applying strategies.
Next up: The next chapters give an in depth overview of the constructs for composing strategies.
Table of Contents
In the previous chapter we saw that pure term rewriting is not adequate for program transformation because of the lack of control over the application of rules. Attempts to encoding such control within the pure rewriting paradigm lead to functionalized control by means of extra rules and constructors at the expense of traversal overhead and at the loss of the separation of rules and strategies. By selecting the appropriate rules and strategy for a transformation, Stratego programmers can control the application of rules, while maintaining the separation of rules and strategies and keeping traversal overhead to a minimum.
We saw that many transformation problems can be solved by alternative strategies such as a one-pass bottom-up or top-down traversals. Others can be solved by selecting the rules that are applied in an innermost normalization, rather than all the rules in a specification. However, no fixed set of such alternative strategies will be sufficient for dealing with all transformation problems. Rather than providing one or a few fixed collection of rewriting strategies, Stratego supports the composition of strategies from basic building blocks with a few fundamental operators.
While we have seen rules and strategies in the previous chapters, we have been vague about what kinds of things they are. In this chapter we define the basic notions of rules and strategies, and we will see how new strategies and strategy combinators can be defined. The next chapters will then introduce the basic combinators used for composition of strategies.
A named rewrite rule is a declaration of the form
L : p1 -> p2
where L is the rule name, p1 the left-hand
side term pattern, and p2 the right-hand side term
pattern.
A rule defines a transformation on terms.
A rule can be applied through its name to a
term.
It will transform the term if it matches with p1, and
will replace the term with p2 instantiated with the
variables bound during the match to p1.
The application fails if the term does not
match p1.
Thus, a transformation is a partial
function from terms to terms
Let's look at an example. The SwapArgs rule swaps the
subterms of the Plus constructor. Note that it is
possible to introduce rules on the fly in the Stratego Shell.
stratego> SwapArgs : Plus(e1,e2) -> Plus(e2,e1)
Now we create a new term, and apply the SwapArgs rule
to it by calling its name at the prompt. (The build !t
of a term replaces the current term by t, as will be
explained in Chapter 16.)
stratego>!Plus(Var("a"),Int("3")) Plus(Var("a"),Int("3"))stratego>SwapArgs Plus(Int("3"),Var("a"))
The application of SwapArgs fails when applied to a
term to which the left-hand side does not match. For example, since
the pattern Plus(e1,e2) does not match with a term
constructed with Times the following application fails:
stratego>!Times(Int("4"),Var("x")) Times(Int("4"),Var("x"))stratego>SwapArgs command failed
A rule is applied at the root of a term, not at
one of its subterms. Thus, the following application fails even
though the term contains a Plus
subterm:
stratego>!Times(Plus(Var("a"),Int("3")),Var("x")) Times(Plus(Var("a"),Int("3")),Var("x"))stratego>SwapArgs command failed
Likewise, the following application only transforms the outermost
occurrence of Plus, not the inner occurrence:
stratego>!Plus(Var("a"),Plus(Var("x"),Int("42"))) Plus(Var("a"),Plus(Var("x"),Int("42")))stratego>SwapArgs Plus(Plus(Var("x"),Int("42")),Var("a"))
Finally, there may be multiple rules with the same name. This has
the effect that all rules with that name will be tried in turn until
one succeeds, or all fail. The rules are tried in some undefined
order. This means that it only makes sense to define rules with the
same name if they are mutually exclusive, that is, do not have
overlapping left-hand sides. For example, we can extend the
definition of SwapArgs with a rule for the
Times constructor, as follows:
stratego> SwapArgs : Times(e1, e2) -> Times(e2, e1)
Now the rule can be applied to terms with a Plus
and a Times constructor, as
illustrated by the following applications:
stratego>!Times(Int("4"),Var("x")) Times(Int("4"),Var("x"))stratego>SwapArgs Times(Var("x"),Int("4"))stratego>!Plus(Var("a"),Int("3")) Plus(Var("a"),Int("3"))stratego>SwapArgs Plus(Int("3"),Var("a"))
Later we will see that a rule is nothing more than a syntactical convention for a strategy definition.
A rule defines a transformation, that is, a partial function from terms to terms. A strategy expression is a combination of one or more transformations into a new transformation. So, a strategy expression also defines a transformation, i.e., a partial function from terms to terms. Strategy operators are functions from transformations to transformations.
In the previous
chapter we saw some examples of strategy expressions.
Lets examine these examples in the light of our new definition.
First of all, rule names are basic strategy
expressions. If we import module prop-laws, we have at
our disposal all rules it defines as basic strategies:
stratego>import prop-lawsstratego>!Impl(True(), Atom("p")) Impl(True, Atom("p"))stratego>DefI Or(Not(True),Atom("p"))
Next, given a collection of rules we can create more complex
transformations by means of strategy operators. For example, the
innermost strategy creates from a collection of rules a
new transformation that exhaustively applies those rules.
stratego>!Eq(Atom("p"), Atom("q")) Eq(Atom("p"),Atom("q"))stratego>innermost(DefI <+ DefE <+ DAOL <+ DAOR <+ DN <+ DMA <+ DMO) Or(Or(And(Not(Atom("p")),Not(Atom("q"))), And(Not(Atom("p")),Atom("p"))), Or(And(Atom("q"),Not(Atom("q"))), And(Atom("q"),Atom("p"))))
(Exercise: add rules to this composition that remove tautologies or
false propositions.)
Here we see that the rules are first combined using the choice
operator <+ into a composite transformation, which
is the argument of the innermost strategy.
The innermost strategy always succeeds (but may not
terminate), but this is not the case for all strategies.
For example bottomup(DefI) will not succeed, since it
attempts to apply rule DefI to all subterms, which is
clearly not possible.
Thus, strategies extend the property of rules that they are
partial functions from terms to terms.
Observe that in the composition innermost(...), the
term to which the transformation is applied is never mentioned.
The `current term', to which a transformation is applied is
often implicit in the definition of a strategy.
That is, there is no variable that is bound to the current term and
then passed to an argument strategy.
Thus, a strategy operator such as innermost is a
function from transformations to transformations.
While strategies are functions, they are not necessarily
pure functions. Strategies in Stratego may
have side effects such as performing input/output operations.
This is of course necessary in the implementation of basic tool
interaction such as provided by io-wrap, but is also
useful for debugging. For example, the debug strategy
prints the current term, but does not transform it. We can use it to
visualize the way that innermost transforms a term.
stratego>!Not(Impl(Atom("p"), Atom("q"))) Not(Impl(Atom("p"),Atom("q")))stratego>innermost(debug(!"in: "); (DefI <+ DefE <+ DAOL <+ DAOR <+ DN <+ DMA <+ DMO); debug(!"out: ")) in: p in: Atom("p") in: q in: Atom("q") in: Impl(Atom("p"),Atom("q")) out: Or(Not(Atom("p")),Atom("q")) in: p in: Atom("p") in: Not(Atom("p")) in: q in: Atom("q") in: Or(Not(Atom("p")),Atom("q")) in: Not(Or(Not(Atom("p")),Atom("q"))) out: And(Not(Not(Atom("p"))),Not(Atom("q"))) in: p in: Atom("p") in: Not(Atom("p")) in: Not(Not(Atom("p"))) out: Atom("p") in: p in: Atom("p") in: q in: Atom("q") in: Not(Atom("q")) in: And(Atom("p"),Not(Atom("q"))) And(Atom("p"),Not(Atom("q")))
This session nicely shows how innermost traverses the term it
transforms. The in: lines show terms to which it
attempts to apply a rule, the out: lines indicate when
this was successful and what the result of applying the rule was.
Thus, innermost performs a post-order traversal
applying rules after transforming the subterms of a term.
(Note that when applying debug to a string constant,
the quotes are not printed.)
Stratego programs are about defining transformations in the form of rules and strategy expressions that combine them. Just defining strategy expressions does not scale, however. Strategy definitions are the abstraction mechanism of Stratego and allow naming and parameterization of strategy expresssions for reuse.
A simple strategy definition names a strategy expression. For
instance, the following module defines a combination of rules
(dnf-rules), and some strategies based on it:
module dnf-strategies
imports libstrategolib prop-dnf-rules
strategies
dnf-rules =
DefI <+ DefE <+ DAOL <+ DAOR <+ DN <+ DMA <+ DMO
dnf =
innermost(dnf-rules)
dnf-debug =
innermost(debug(!"in: "); dnf-rules; debug(!"out: "))
main =
io-wrap(dnf)
Note how dnf-rules is used in the definition of
dnf, and dnf itself in the definition of
main.
In general, a definition of the form
f = s
introduces a new transformation f, which can be invoked
by calling f in a strategy expression, with the effect
of executing strategy expression s.
The expression should have no free variables. That is, all strategie
called in s should be defined strategies.
Simple strategy definitions just introduce names for strategy
expressions.
Still such strategies have an argument, namely the implicit current
term.
Strategy definitions with strategy and/or term parameters can be used to define transformation schemas that can instantiated for various situations.
A parameterized strategy definition of the form
f(x1,...,xn | y1,..., ym) = s
introduces a user-defined operator f with
n strategy arguments and
m term arguments. Such a
user-defined strategy operator can be called as
f(s1,...,sn|t1,...,tm) by providing it n
argument strategies and m argument terms. The meaning
of such a call is the body s of the definition in which
the actual arguments have been substituted for the formal arguments.
Strategy arguments and term arguments can be left out of calls and
definitions. That is, a call f(|) without strategy and
term arguments can be written as f(), or even just
f. A call f(s1,..., sn|) without term
arguments can be written as f(s1,...,sn) The same holds
for definitions.
As we will see in the coming chapters, strategies such as
innermost, topdown, and
bottomup are not built into the
language, but are defined using strategy definitions in
the language itself using more basic combinators, as illustrated by
the following definitions (without going into the exact meaning of
these definitions):
strategies try(s) = s <+ id repeat(s) = try(s; repeat(s)) topdown(s) = s; all(topdown(s)) bottomup(s) = all(bottomup(s)); s
Such parameterized strategy operators are invoked by providing
arguments for the parameters. Specifically, strategy arguments are
instantiated by means of strategy expressions. Wherever the argument
is invoked in the body of the definition, the strategy expression is
invoked.
For example, in the previous chapter we
saw the following instantiations of the topdown,
try, and repeat strategies:
module prop-desugar
// ...
strategies
desugar =
topdown(try(DefI <+ DefE))
impl-nf =
topdown(repeat(DefN <+ DefA2 <+ DefO1 <+ DefE))
There can be multiple definitions with the same name but different numbers of parameters. Such definitions introduce different strategy operators.
Strategy definitions at top-level are visible everywhere. Sometimes
it is useful to define a local strategy
operator. This can be done using a let expression of the form
let d* in s end, where d* is a list of
definitions.
For example, in the following strategy expression, the definition of
dnf-rules is only visible in the instantiation of
innermost:
let dnf-rules = DefI <+ DefE <+ DAOL <+ DAOR <+ DN <+ DMA <+ DMO in innermost(dnf-rules) end
The current version of Stratego does not support hidden strategy definitions at the module level. Such a feature is under consideration for a future version.
As we saw in Chapter 12, a Stratego program can introduce several rules with the same name. It is even possible to extend rules across modules. This is also possible for strategy definitions. If two strategy definitions have the same name and the same number of parameters, they effectively define a single strategy that tries to apply the bodies of the definitions in some undefined order. Thus, a definition of the form
strategies f = s1 f = s2
entails that a call to f has the effect of first trying
to apply s1, and if that fails applies s2,
or the other way around. Thus, the definition above is either
translated to
strategies f = s1 <+ s2
or to
strategies f = s2 <+ s1
Stratego provides combinators for composing transformations and
basic operators for analyzing, creating and traversing
terms. However, it does not provide built-in support for other types
of computation such as input/output and process control. In order to
make such functionality available to Stratego programmers, the
language provides access to user-definable
primitive strategies through the
prim construct. For example, the following call to
prim invokes the SSL_printnl function from
the native code of the C library:
stratego> prim("SSL_printnl", stdout(), ["foo", "bar"])
foobar
""
In general, a call prim("f", s* | t*) represents a call
to a primitive function f with
strategy arguments s* and term arguments
t*.
Note that the `current' term is not passed automatically as
argument.
This mechanism allows the incorporation of mundane tasks such as arithmetic, I/O, and other tasks not directly related to transformation, but necessary for the integration of transformations with the other parts of a transformation system.
Primitive functions should take ATerms as arguments. It is not
possible to use `unboxed' values, i.e., raw native types. This
requires writing a wrapper function in C. For example, the addition
of two integers is defined via a call to a primitive
prim("SSL_addi",x,y), where the argument should
represent integer ATerms, not C integers.
Implementing Primitives. The Stratego Library provides all the primitives for I/O, arithmetic, string processing, and process control that are usually needed in Stratego programs. However, it is possible to add new primitives to a program as well. That requires linking with the compiled program a library that implements the function. See the documentation of strc for instructions.
The Stratego Compiler is a whole program compiler. That is, the compiler includes all definitions from imported modules (transitively) into the program defined by the main module (the one being compiled). This is the reason that the compiler takes its time to compile a program. To reduce the compilation effort and the size of the resulting programs it is possible to create separately compiled libraries of Stratego definitions. The strategies that such a library provides are declared as external definitions. A declaration of the form
external f(s1 ... sn | x1 ... xm)
states that there is an externally defined strategy operator
f with n strategy arguments and
m term arguments. When compiling a program with
external definitions a library should be provided that implements
these definitions.
The Stratego Library is provided as a separately compiled library.
The libstrateglib module that we have been using in the
example programs contains external definitions for all strategies in
the library, as illustrated by the following excerpt:
module libstrategolib // ... strategies // ... external io-wrap(s) external bottomup(s) external topdown(s) // ...
When compiling a program using the library we used the -la
stratego-lib option to provide the implementation of those
definitions.
External Definitions cannot be Extended. Unlike definitions imported in the normal way, external definitions cannot be extended. If we try to compile a module extending an external definition, such as
module wrong imports libstrategolib strategies bottomup(s) = fail
compilation fails:
$ strc -i wrong.str
[ strc | info ] Compiling 'wrong.str'
error: redefining external definition: bottomup/1-0
[ strc | error ] Compilation failed (3.66 secs)
Creating Libraries.
It is possible to create your own Stratego libraries as
well. Currently that exposes you to a bit of C compilation giberish;
in the future this may be incorporated in the Stratego compiler.
Lets create a library for the rules and strategy definitions in the
prop-laws module. We do this using the
--library option to indicate that a library is being
built, and the -c option to indicate that we are only
interested in the generated C code.
$strc -i prop-laws.str -c -o libproplib.rtree --library [ strc | info ] Compiling 'proplib.str' [ strc | info ] Front-end succeeded : [user/system] = [4.71s/0.77s] [ strc | info ] Abstract syntax in 'libproplib.rtree' [ strc | info ] Concrete syntax in 'libproplib.str' [ strc | info ] Export of externals succeeded : [user/system] = [2.02s/0.11s] [ strc | info ] Back-end succeeded : [user/system] = [6.66s/0.19s] [ strc | info ] Compilation succeeded : [user/system] = [13.4s/1.08s]$rm libproplib.str
The result is of this compilation is a module
libproplib that contains the external definitions of
the module and those inherited from
libstrategolib. (This module comes in to versions; one
in concrete syntax libproplib.str and one in abstract
syntax libproplib.rtree; for some obscure reason you
should throw away the .str file.)
Furthermore, the Stratego Compiler produces a C program
libproplib.c with the implementation of the
library. This C program should be turned into an object library
using libtool, as follows:
$libtool --mode=compile gcc -g -O -c libproplib.c -o libproplib.o -I <path/to/aterm-stratego/include> ...$libtool --mode=link gcc -g -O -o libproplib.la libproplib.lo ...
The result is a shared library libproplib.la that can
be used in other Stratego programs.
(TODO: the production of the shared library should really be
incorporated into strc.)
Using Libraries. Programmers that want to use your library can now import the module with external definitions, instead of the original module.
module dnf-tool imports libproplib strategies main = main-dnf
This program can be compiled in the usual way, adding the new library to the libraries that should be linked against:
$strc -i dnf-tool.str -la stratego-lib -la ./libproplib.la$cat test3.prop And(Impl(Atom("r"),And(Atom("p"),Atom("q"))),ATom("p"))$./dnf-tool -i test3.prop Or(And(Not(Atom("r")),ATom("p")),And(And(Atom("p"),Atom("q")),ATom("p")))
To correctly deploy programs based on shared libraries requires some additional effort. Chapter 29 explains how to create deployable packages for your Stratego programs.
Strategies can be called dynamically by name, i.e., where the name
of the strategy is specified as a string. Such calls can be made
using the call construct, which has the form:
call(f | s1, ..., sn | t1, ..., tn)
where f is a term that should evaluate to a string,
which indicates the name of the strategy to be called, followed by a
list of strategy arguments, and a list of term arguments.
Dynamic calls allow the name of the strategy to be computed at run-time. This is a rather recent feature of Stratego that was motivated by the need for call-backs from a separately compiled Stratego library combined with the computation of dynamic rule names. Otherwise, there is not yet much experience with the feature.
In the current version of Stratego it is necessary to 'register' a
strategy to be able to call it dynamically. (In order to avoid
deletion in case it is not called explicitly somewhere in the
program.) Strategies are registered by means of a dummy strategy
definition DYNAMIC-CALLS with calls to the strategies
that should called dynamically.
DYNAMICAL-CALLS = foo(id)
We have learned that rules and strategies define transformations, that is, functions from terms to terms that can fail, i.e., partial functions. Rule and strategy definitions introduce names for transformations. Parameterized strategy definitions introduce new strategy operators, functions that construct transformations from transformations.
Primitive strategies are transformations that are implemented in
some language other than Stratego (usually C), and are called
through the prim construct.
External definitions define an interface to a separately compiled
library of Stratego definitions.
Dynamic calls allow the name of the strategy to be called to be
computed as a string.
Table of Contents
We have seen the use of strategies to combine rules into complex
transformations.
Rather than providing a fixed set of high-level strategy operators
such as bottomup, topdown, and
innermost, Stratego provides a small set of basic
combinators, that can be used to create a wide variety of
strategies.
In Chapter 15 until Chapter 18 we will introduce these
combinators.
In this chapter we start with a set of combinators for sequential
composition and choice of strategies.
The most basic operations in Stratego are id and
fail.
The identity strategy id always succeeds and behaves as
the identity function on terms.
The failure strategy fail always fails.
The operations have no side effects.
stratego>!Foo(Bar()) Foo(Bar)stratego>id Foo(Bar)stratego>fail command failed
The sequential composition s1 ; s2 of the strategies
s1 and s2 first applies the strategy
s1 to the subject term and then s2 to the
result of that first application. The strategy fails if either
s1 or s2 fails.
Properties.
Sequential composition is associative. Identity is a left and right
unit for sequential composition; since id always
succeeds and leaves the term alone, it has no additional effect to
the strategy that it is composed with. Failure is a left zero for
sequential composition; since fail always fails the
next strategy will never be reached.
(s1; s2) ; s3 = s1; (s2; s3) id; s = s s; id = s fail; s = fail
However, not for all strategies s we have that failure
is a right zero for sequential composition:
s ; fail = fail (is not a law)
Although the composition s; fail will always fail, the
execution of s may have side effects that are not
performed by fail. For example, consider printing a
term in s.
Examples. As an example of the use of sequential composition consider the following rewrite rules.
stratego>A : P(Z(),x) -> xstratego>B : P(S(x),y) -> P(x,S(y))
The following session shows the effect of first applying
B and then A:
stratego>!P(S(Z()), Z()) P(S(Z),Z)stratego>B P(Z,S(Z))stratego>A S(Z)
Using the sequential composition of the two rules, this effect can be achieved `in one step':
stratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>B; A S(Z)
The following session shows that the application of a composition fails if the second strategy in the composition fails to apply to the result of the first:
stratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>B; B command failed
Choosing between rules to apply is achieved using one of several choice combinators, all of which are based on the guarded choice combinator. The common approach is that failure to apply one strategy leads to backtracking to an alternative strategy.
The left choice or deterministic choice s1 <+ s2
tries to apply s1 and s2 in that
order. That is, it first tries to apply s1, and if that
succeeds the choice succeeds. However, if the application of
s1 fails, s2 is applied to the
original term.
Properties.
Left choice is associative. Identity is a left zero for left choice;
since id always succeeds, the alternative strategy will
never be tried. Failure is a left and right unit for left choice;
since fail always fails, the choice will always
backtrack to the alternative strategy, and use of fail
as alternative strategy is pointless.
(s1 <+ s2) <+ s3 = s1 <+ (s2 <+ s3) id <+ s = id fail <+ s = s s <+ fail = s
However, identity is not a right zero for left choice. That is,
not for all strategies s we have that
s <+ id = s (is not a law)
The expression s <+ id always succeeds, even
(especially) in the case that s fails, in which case
the right-hand side of the equation fails of course.
Local Backtracking. The left choice combinator is a local backtracking combinator. That is, the choice is committed once the left-hand side strategy has succeeded, even if the continuation strategy fails. This is expressed by the fact that the property
(s1 <+ s2); s3 = (s1; s3) <+ (s2; s3) (is not a law)
does not hold for all s1,
s2, and s3.
The difference is illustrated by the following applications:
stratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>(B <+ id); B command failedstratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>(B <+ id) P(Z,S(Z))stratego>B command failedstratego>(B; B) <+ (id; B) P(Z,S(Z))
In the application of (B <+ id); B, the first
application of B succeeds after which the choice is
committed. The subsequent application of B then fails.
This equivalent to first applying (B <+ id) and then
applying B to the result.
The application of (B; B) <+ (id; B), however, is
successful; the application of B; B fails, after which
the choice backtracks to id; B, which succeeds.
Choosing between Transformations. The typical use of left choice is to create a composite strategy trying one from several possible transformations. If the strategies that are composed are mutually exclusive, that is, don't succeed for the same terms, their sum is a transformation that (deterministically) covers a larger set of terms. For example, consider the following two rewrite rules:
stratego>PlusAssoc : Plus(Plus(e1, e2), e3) -> Plus(e1, Plus(e2, e3))stratego>PlusZero : Plus(Int("0"),e) -> e
These rules are mutually exclusive, since there is no term that
matches the left-hand sides of both rules. Combining the rules with
left choice into PlusAssoc <+ PlusZero creates a
strategy that transforms terms matching both rules as illustrated by
the following applications:
stratego>!Plus(Int("0"),Int("3")) Plus(Int("0"),Int("3"))stratego>PlusAssoc command failedstratego>PlusAssoc <+ PlusZero Int("3")stratego>!Plus(Plus(Var("x"),Int("42")),Int("3")) Plus(Plus(Var("x"),Int("42")),Int("3"))stratego>PlusZero command failedstratego>PlusAssoc <+ PlusZero Plus(Var("x"),Plus(Int("42"),Int("3")))
Ordering Overlapping Rules.
When two rules or strategies are mutually exlusive the order of
applying them does not matter.
In cases where strategies are overlapping, that is, succeed for the
same terms, the order becomes crucial to determining the semantics
of the composition.
For example, consider the following rewrite rules reducing
applications of Mem:
stratego>Mem1 : Mem(x,[]) -> False()stratego>Mem2 : Mem(x,[x|xs]) -> True()stratego>Mem3 : Mem(x,[y|ys]) -> Mem(x,ys)
Rules Mem2 and Mem3 have overlapping
left-hand sides. Rule Mem2 only applies if the first
argument is equal to the head element of the list in the second
argument. Rule Mem3 applies always if the list in the
second argument is non-empty.
stratego>!Mem(1, [1,2,3]) Mem(1, [1,2,3])stratego>Mem2 Truestratego>!Mem(1, [1,2,3]) Mem(1,[1,2,3])stratego>Mem3 Mem(1,[2,3])
In such situations, depending on the order of the rules, differents
results are produced. (The rules form a non-confluent rewriting
system.)
By ordering the rules as Mem2 <+ Mem3, rule
Mem2 is tried before Mem3, and we have a
deterministic transformation strategy.
Try.
A useful application of <+ in combination with
id is the reflexive closure of a strategy
s:
try(s) = s <+ id
The user-defined strategy combinator try tries to apply
its argument strategy s, but if that fails, just
succeeds using id.
Sometimes it is not desirable to backtrack to the alternative
specified in a choice. Rather, after passing a
guard, the choice should be committed. This can
be expressed using the guarded left choice
operator s1 < s2 + s3.
If s1 succeeds s2 is applied, else
s3 is applied. If s2 fails, the complete
expression fails; no backtracking to s3 takes place.
Properties.
This combinator is a generalization of the left choice combinator
<+.
s1 <+ s2 = s1 < id + s2
The following laws make clear that the `branches' of the choice are selected by the success or failure of the guard:
id < s2 + s3 = s2 fail < s2 + s3 = s3
If the right branch always fails, the construct reduces to the sequential composition of the guard and the left branch.
s1 < s2 + fail = s1; s2
Guarded choice is not associative:
(s1 < s2 + s3) < s4 + s5 = s1 < s2 + (s3 < s4 + s5) (not a law)
To see why consider the possible traces of these expressions. For example,
when s1 and s2 succeed subsequently, the left-hand
side expression calls s4, while the right-hand side expression does
not.
However, sequential composition distributes over guarded choice from left and right:
(s1 < s2 + s3); s4 = s1 < (s2; s4) + (s3; s4) s0; (s1 < s2 + s3) = (s0; s1) < s2 + s3
Examples.
The guarded left choice operator is most useful for the
implementation of higher-level control-flow strategies.
For example, the negation not(s)
of a strategy s, succeeds if s fails, and
fails when it succeeds:
not(s) = s < fail + id
Since failure discards the effect of a (succesful) transformation,
this has the effect of testing whether s succeeds. So
we have the following laws for not:
not(id) = fail not(fail) = id
However, side effects performed by s are not undone, of
course. Therefore, the following equation does
not hold:
not(not(s)) = s (not a law)
Another example of the use of guarded choice is the
restore-always combinator:
restore-always(s, r) = s < r + (r; fail)
It applies a `restore' strategy r after applying a
strategy s, even if s fails, and preserves
the success/failure behaviour of s. Since
fail discards the transformation effect of
r, this is mostly useful for ensuring that some
side-effecting operation is done (or undone) after applying
s.
For other applications of guarded choice, Stratego provides syntactic sugar.
The guarded choice combinator is similar to the traditional
if-then-else construct of programming languages. The difference is
that the `then' branch applies to the result of the application of
the condition.
Stratego's if s1 then s2 else s3 end construct is more
like the traditional construct since both branches apply to the
original term. The condition strategy is only used to test if it
succeeds or fails, but it's transformation effect is
undone. However, the condition strategy s1 is still
applied to the current term.
The if s1 then s2 end strategy is similar; if the
condition fails, the strategy succeeds.
Properties.
The if-then-else-end strategy is just syntactic sugar
for a combination of guarded choice and the where
combinator:
if s1 then s2 else s3 end = where(s1) < s2 + s3
The strategy where(s) succeeds if s
succeeds, but returns the original subject term. The implementation
of the where combinator will be discussed in Chapter 16.
The following laws show that the branches are selected by success or
failure of the condition:
if id then s2 else s3 end = s2 if fail then s2 else s3 end = s3
The if-then-end strategy is an abbreviation for the
if-then-else-end with the identity strategy as right
branch:
if s1 then s2 end = where(s1) < s2 + id
Examples.
The inclusive or or(s1, s2)
succeeds if one of the strategies s1 or s2
succeeds, but guarantees that both are applied, in the order
s1 first, then s2:
or(s1, s2) = if s1 then try(where(s2)) else where(s2) end
This ensures that any side effects are always performed, in contrast
to s1 <+ s2, where s2 is only executed
if s1 fails. (Thus, left choice implements a short
circuit Boolean or.)
Similarly, the following and(s1, s2) combinator is the
non-short circuit version of Boolean conjunction:
and(s1, s2) = if s1 then where(s2) else where(s2); fail end
The switch construct is an n-ary branching construct
similar to its counter parts in other programming languages. It is
defined in terms of guarded choice.
The switch construct has the following form:
switch s0
case s1 : s1'
case s2 : s2'
...
otherwise : sdef
end
The switch first applies the s0 strategy to the current
term t resulting in a term t'. Then it
tries the cases in turn applying each si to
t'. As soon as this succeeds the corresponding case is
selected and si' is applied to the t, the
term to which the switch was applied. If none of the cases applies,
the default strategy sdef from the
otherwise is applied.
Properties. The switch construct is syntactic sugar for a nested if-then-else:
{x : where(s0 => x);
if <s1> x
then s1'
else if <s2> x
then s2'
else if ...
then ...
else sdef
end
end
end}
This translation uses a couple of Stratego constructs that we haven't discussed so far.
Examples. TODO
The deterministic left choice operator prescribes that the left alternative should be tried before the right alternative, and that the latter is only used if the first fails. There are applications where it is not necessary to define the order of the alternatives. In those cases non-deterministic choice can be used.
The non-deterministic choice operator s1 + s2 chooses
one of the two strategies s1 or s2 to
apply, such that the one it chooses succeeds. If both strategies
fail, then the choice fails as well.
Operationally the choice operator first tries one strategy, and, if
that fails, tries the other. The order in which this is done is
undefined, i.e., arbitrarily chosen by the compiler.
The + combinator is used to model modular composition
of rewrite rules and strategies with the same name. Multiple
definitions with the same name, are merged into a single definition
with that name, where the bodies are composed with
+. The following transformation illustrates this:
f = s1 f = s2 ==> f = s1 + s2
This transformation is somewhat simplified; the complete transformation needs to take care of local variables and parameters.
While the + combinator is used internally by the
compiler for this purpose, programmers are advised
not to use this combinator, but rather use the
left choice combinator <+ to avoid surprises.
Repeated application of a strategy can be achieved with recursion.
There are two styles for doing this; with a recursive definition or
using the fixpoint operator rec. A recursive
definition is a normal strategy definition with a recursive call in
its body.
f(s) = ... f(s) ...
Another way to define recursion is using the fixpoint operator
rec x(s), which recurses on applications of
x within s. For example, the definition
f(s) = rec x(... x ...)
is equivalent to the one above.
The advantage of the rec operator is that it allows
the definition of an unnamed strategy expression to be recursive.
For example, in the definition
g(s) = foo; rec x(... x ...); bar
the strategy between foo and bar is a
recursive strategy that does not recurse to
g(s).
Originally, the rec operator was the only way to
define recursive strategies. It is still in the language in the
first place because it is widely used in many existing programs,
and in the second place because it can be a concise expression of a
recursive strategy, since call parameters are not included in the
call. Furthermore, all free variables remain in scope.
Examples.
The repeat strategy applies a transformation
s until it fails. It is defined as a recursive
definition using try as follows:
try(s) = s <+ id repeat(s) = try(s; repeat(s))
An equivalent definition using rec is:
repeat(s) = rec x(try(s; x))
The following Stratego Shell session illustrates how it works. We first define the strategies:
stratego>try(s) = s <+ idstratego>repeat(s) = try(s; repeat(s))stratego>A : P(Z(),x) -> xstratego>B : P(S(x),y) -> P(x,S(y))
Then we observe that the repeated application of the individual
rules A and B reduces terms:
stratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>B P(Z,S(Z))stratego>A S(Z)
We can automate this using the repeat strategy, which
will repeat the rules as often as possible:
stratego>!P(S(Z()),Z()) P(S(Z),Z)stratego>repeat(A <+ B) S(Z)stratego>!P(S(S(S(Z()))),Z()) P(S(S(S(Z))),Z)stratego>repeat(A <+ B) S(S(S(Z)))
To illustrate the intermediate steps of the transformation we can
use debug from the Stratego Library.
stratego>import liblibstratego>!P(S(S(S(Z()))),Z()) P(S(S(S(Z))),Z)stratego>repeat(debug; (A <+ B)) P(S(S(S(Z))),Z) P(S(S(Z)),S(Z)) P(S(Z),S(S(Z))) P(Z,S(S(S(Z)))) S(S(S(Z))) S(S(S(Z)))
A Library of Iteration Strategies.
Using sequential composition, choice, and recursion a large
variety of iteration strategies can be defined. The following
definitions are part of the Stratego Library (in module
strategy/iteration).
repeat(s) = rec x(try(s; x)) repeat(s, c) = (s; repeat(s, c)) <+ c repeat1(s, c) = s; (repeat1(s, c) <+ c) repeat1(s) = repeat1(s, id) repeat-until(s, c) = s; if c then id else repeat-until(s, c) end while(c, s) = if c then s; while(c, s) end do-while(s, c) = s; if c then do-while(s, c) end
The following equations describe some relations between these strategies:
do-while(s, c) = repeat-until(s, not(c)) do-while(s, c) = s; while(c, s)
We have seen that rules and strategies can be combined into more
complex strategies by means of strategy combinators.
Cumulative effects are obtained by sequential composition of
strategies using the s1 ; s2 combinator.
Choice combinators allow a strategy to decide between alternative
transformations. While Stratego provides a variety of choice
combinators, they are all based on the guarded choice combinator
s1 < s2 + s3.
Repetition of transformations is achieved using recursion, which can
be achieved through recursive definitions or the rec
combinator.
Next up: Chapter 16 shows the stuff that rewrite rules are made of.
Table of Contents
In previous chapters we have presented rewrite rules as basic transformation steps. However, rules are not really atomic transformation actions. To see this, consider what happens when the rewrite rule
DAOL : And(Or(x, y), z) -> Or(And(x, z), And(y, z))
is applied. First it matches the subject term against the pattern
And(Or(x, y), z) in the left-hand side. This means that
a substitution for the variables x, y, and
z is sought, that makes the pattern equal to the
subject term. If the match fails, the rule fails. If the match
succeeds, the pattern Or(And(x, z), And(y, z)) on the
right-hand side is instantiated with the bindings found during the
match of the left-hand side. The instantiated term then replaces the
original subject term. Furthermore, the rule limits the scope of the
variables occurring in the rule. That is, the variables
x, y, z are local to this
rule. After the rule is applied the bindings to these variables are
invisible again.
Thus, rather than considering rules as the atomic actions of transformation programs, Stratego provides their constituents, that is building terms from patterns and matching terms against patterns, as atomic actions, and makes these available to the programmer. In this chapter, you will learn these basic actions and their use in the composition of more complex operations such as various flavours of rewrite rules.
The build operation !p replaces the subject term with
the instantiation of the pattern p using the bindings
from the environment to the variables occurring in p.
For example, the strategy !Or(And(x, z), And(y, z))
replaces the subject term with the instantiation of
Or(And(x, z), And(y, z)) using bindings to variables
x, y and z.
stratego>!Int("10") Int("10")stratego>!Plus(Var("a"), Int("10")) Plus(Var("a"), Int("10"))
It is possible to build terms with variables. We call this
building a term pattern. A pattern is a term with
meta-variables. The current term is replaced
by an instantiation of pattern p.
stratego>:binding e e is bound to Var("b")stratego>!Plus(Var("a"),e) Plus(Var("a"),Var("b"))stratego>!e Var("b")
Pattern matching allows the analysis of terms. The simplest case
is matching against a literal term.
The match operation ?t matches the subject term
against the term t.
Plus(Var("a"),Int("3"))
stratego> ?Plus(Var("a"),Int("3"))
stratego> ?Plus(Int("3"),Var("b"))
command failed
Matching against a term pattern with
variables binds those variables to (parts of) the current term.
The match strategy ?
compares the current term (xt) to
variable x. It binds variable
x to term t
in the environment. A variable can only be bound once, or to the
same term.
Plus(Var("a"),Int("3"))
stratego> ?e
stratego> :binding e
e is bound to Plus(Var("a"),Int("3"))
stratego> !Int("17")
stratego> ?e
command failed
The general case is matching against an arbitrary term pattern.
The match strategy ?
compares the current term to a pattern
pp. It will add bindings for the
variables in pattern p to the
environment. The wildcard _ in a match will match any
term.
Plus(Var("a"),Int("3"))
stratego> ?Plus(e,_)
stratego> :binding e
e is bound to Var("a")
Plus(Var("a"),Int("3"))
Patterns may be non-linear. Multiple occurences of the same variable can occur and each occurence matches the same term.
Plus(Var("a"),Int("3"))
stratego> ?Plus(e,e)
command failed
stratego> !Plus(Var("a"),Var("a"))
stratego> ?Plus(e,e)
stratego> :binding e
e is bound to Var("a")
Non-linear pattern matching is a way to test equality of terms. Indeed the equality predicates from the Stratego Library are defined using non-linear pattern matching:
equal = ?(x, x) equal(|x) = ?x
The equal strategy tests whether the current term is a
a pair of the same terms.
The equal(|x) strategy tests whether the current term
is equal to the argument term.
stratego>equal = ?(x, x)stratego>!("a", "a") ("a", "a")stratego>equal ("a", "a")stratego>!("a", "b") ("a", "b")stratego>equal command failedstratego>equal(|x) = ?xstratego>!Foo(Bar()) Foo(Bar)stratego>equal(|Foo(Baz())) command failedstratego>equal(|Foo(Bar())) Foo(Bar)
Match and build are first-class citizens in Stratego, which means that they can be used and combined just like any other strategy expressions. In particular, we can implement rewrite rules using these operations, since a rewrite rule is basically a match followed by a build. For example, consider the following combination of match and build:
Plus(Var("a"),Int("3"))
stratego> ?Plus(e1, e2); !Plus(e2, e1)
Plus(Int("3"),Var("a"))
This combination first recognizes a term, binds variables to the pattern in the match, and then replaces the current term with the instantiation of the build pattern. Note that the variable bindings are propagated from the match to the build.
Stratego provides syntactic sugar for various combinations of match and build. We'll explore these in the rest of this chapter.
An anonymous rewrite rule (p1 ->
p2) transforms a term matching p1 into an
instantiation of p2.
Such a rule is equivalent to the sequence ?p1; !p2.
Plus(Var("a"),Int("3"))
stratego> (Plus(e1, e2) -> Plus(e2, e1))
Plus(Int("3"),Var("a"))
Once a variable is bound it cannot be rebound to a different
term. Thus, once we have applied an anonymous rule once, its
variables are bound and the next time it is applied it only
succeeds for the same term. For example, in the next session the
second application of the rule fails, because e2 is
bound to Int("3") and does not match with
Var("b").
stratego>!Plus(Var("a"),Int("3")) Plus(Var("a"),Int("3"))stratego>(Plus(e1,e2) -> Plus(e2,e1)) Plus(Int("3"),Var("a"))stratego>:binding e1 e1 is bound to Var("a")stratego>:binding e2 e2 is bound to Int("3")stratego>!Plus(Var("a"),Var("b")) Plus(Var("a"),Var("b"))stratego>(Plus(e1,e2) -> Plus(e2,e1)) command failed
To use a variable name more than once Stratego provides
term variable scope.
A scope {x1,...,xn : s} locally undefines the
variables xi. That is, the binding to a variable
xi outside the scope is not visible inside it, nor is
the binding to xi inside the scope visible outside
it.
For example, to continue the session above, if we wrap the
anonymous swap rule in a scope for its variables, it can be
applied multiple times.
stratego>!Plus(Var("a"),Int("3")) Plus(Var("a"),Int("3"))stratego>{e3,e4 : (Plus(e3,e4) -> Plus(e4,e3))} Plus(Var("a"),Int("3"))stratego>:binding e3 e3 is not bound to a termstratego>!Plus(Var("a"),Var("b")) Plus(Var("a"),Var("b"))stratego>{e3,e4 : (Plus(e3,e4) -> Plus(e4,e3))} Plus(Var("b"),Var("a"))
Of course we can name such a scoped rule using a strategy definition, and then invoke it by its name:
stratego>SwapArgs = {e1,e2 : (Plus(e1,e2) -> Plus(e2,e1))}stratego>!Plus(Var("a"),Int("3")) Plus(Var("a"),Int("3"))stratego>SwapArgs Plus(Int("3"),Var("a"))
When using match and build directly in a strategy definition, rather than in the form of a rule, the definition contains free variables. Strictly speaking such variables should be declared using a scope, that is one should write
SwapArgs = {e1,e2 : (Plus(e1,e2) -> Plus(e2,e1))}
However, since declaring all variables at the top of a definition is destracting and does not add much to the definition, such a scope declaration can be left out. Thus, one can write
SwapArgs = (Plus(e1,e2) -> Plus(e2,e1))
instead. The scope is automatically inserted by the compiler. This implies that there is no global scope for term variables. Of course, variables in inner scopes should be declared where necessary. In particular, note that variable scope is not inserted for strategy definitions in a let binding, such as
let SwapArgs = (Plus(e1,e2) -> Plus(e2,e1)) in ... end
While the variables are bound in the enclosing definition, they are
not restricted to SwapArgs in this case, since in a let
you typically want to use bindings to variables in the enclosing
code.
Often it is useful to apply a strategy only to test whether some
property holds or to compute some auxiliary result. For this
purpose, Stratego provides the where(s) combinator,
which applies s to the current term, but restores that
term afterwards. Any bindings to variables are kept, however.
Plus(Int("14"),Int("3"))
stratego> where(?Plus(Int(i),Int(j)); <addS>(i,j) => k)
Plus(Int("14"),Int("3"))
stratego> :binding i
i is bound to "14"
stratego> :binding k
k is bound to "17"
With the match and build constructs where(s) is in fact
just syntactic sugar for {x: ?x; s; !x} with
x a fresh variable not occurring in s.
Thus, the current subject term is saved by
binding it to a new variable x, then the strategy
s is applied, and finally, the original term is
restored by building x.
We saw the use of where in the definition of
if-then-else in Chapter 15.
A simple rewrite rule succeeds if the match of the left-hand side
succeeds. Sometimes it is useful to place additional requirements on
the application of a rule, or to compute some value for use in the
right-hand side of the rule. This can be achieved with
conditional rewrite rules.
A conditional rule L: p1 -> p2 where s is a simple rule
extended with an additional computation s which should
succeed in order for the rule to apply.
The condition can be used to test properties of terms in the
left-hand side, or to compute terms to be used in the right-hand
side. The latter is done by binding such new terms to variables used
in the right-hand side.
For example, the EvalPlus rule in the following session
uses a condition to compute the sum of i and
j:
stratego>EvalPlus: Plus(Int(i),Int(j)) -> Int(k) where !(i,j); addS; ?kstratego>!Plus(Int("14"),Int("3")) Plus(Int("14"),Int("3"))stratego>EvalPlus Int("17")
A conditional rule can be desugared similarly to an unconditional rule. That is, a conditional rule of the form
L : p1 -> p2 where s
is syntactic sugar for
L = ?p1; where(s); !p2
Thus, after the match with p1 succeeds the strategy
s is applied to the subject term. Only if the
application of s succeeds, is the right-hand side
p2 built. Note that since s is applied
within a where, the build !p2 is applied
to the original subject term; only variable
bindings computed within s can be used in
p2.
As an example, consider the following constant folding rule, which reduces an addition of two integer constants to the constant obtained by computing the addition.
EvalPlus : Add(Int(i),Int(j)) -> Int(k) where !(i,j); addS; ?k
The addition is computed by applying the primitive strategy
add to the pair of integers (i,j) and
matching the result against the variable k, which is
then used in the right-hand side. This rule is desugared to
EvalPlus = ?Add(Int(i),Int(j)); where(!(i,j); addS; ?k); !Int(k)
Sometimes it is useful to define a rule anonymously within a strategy expression. The syntax for anonymous rules with scopes is a bit much since it requires enumerating all variables. A `lambda' rule of the form
\ p1 -> p2 where s \
is an anonymous rewrite rule for which the variables in the
left-hand side p1 are local to the rule, that is,
it is equivalent to an expression of the form
{x1,...,xn : (p1 -> p2 where s)}
with x1,...,xn the variables of
p1.
This means that any variables used in s and
p2 that do not occur in
p1 are bound in the context of the rule.
A typical example of the use of an anonymous rule is
stratego>![(1,2),(3,4),(5,6)] [(1,2),(3,4),(5,6)]stratego>map(\ (x, y) -> x \ ) [1,3,5]
One frequently occuring scenario is that of applying a strategy to a term and then matching the result against a pattern. This typically occurs in the condition of a rule. In the constant folding example above we saw this scenario:
EvalPlus : Add(Int(i),Int(j)) -> Int(k) where !(i,j); addS; ?k
In the condition, first the term (i,j) is built, then
the strategy addS is applied to it, and finally the
result is matched against the pattern k.
To improve the readability of such expressions, the following two
constructs are provided. The operation <s> p
captures the notion of applying a strategy to a
term, i.e., the scenario !p; s. The operation s
=> p capture the notion of applying a strategy to the current
subject term and then matching the result against the pattern
p, i.e., s; ?p. The combined operation
<s> p1 => p2 thus captures the notion of applying a
strategy to a term p1 and matching the result against
p2, i.e, !t1; s; ?t2. Using this notation
we can improve the constant folding rule above as
EvalPlus : Add(Int(i),Int(j)) -> Int(k) where <add>(i,j) => k
Applying Strategies in Build. Sometimes it useful to apply a strategy directly to a subterm of a pattern, for example in the right-hand side of a rule, instead of computing a value in a condition, binding the result to a variable, and then using the variable in the build pattern. The constant folding rule above, for example, could be further simplified by directly applying the addition in the right-hand side:
EvalPlus : Add(Int(i),Int(j)) -> Int(<add>(i,j))
This abbreviates the conditional rule above. In general, a strategy application in a build pattern can always be expressed by computing the application before the build and binding the result to a new variable, which then replaces the application in the build pattern.
Another example is the following definition of the
map(s) strategy, which applies a strategy to each term
in a list:
map(s) : [] -> [] map(s) : [x | xs] -> [<s> x | <map(s)> xs]
Term wrapping and projection are concise idioms for constructing terms that wrap the current term and for extracting subterms from the current term.
One often write rules of the form \ x -> Foo(Bar(x))\,
i.e. wrapping a term pattern around the current term. Using rule
syntax this is quite verbose. The syntactic abstraction of
term wraps, allows the concise specification of
such little transformations as !Foo(Bar(<id>)).
In general, a term wrap is a build strategy !p[<s>]
containing one or more strategy applications <s>
that are not applied to a term.
When executing the the build operation, each occurrence of such a
strategy application <s> is replaced with the term
resulting from applying s to the current subject term,
i.e., the one that is being replaced by the build.
The following sessions illustrate some uses of term wraps:
3stratego>!(<id>,<id>) (3,3)stratego>!(<Fst; inc>,<Snd>) (4,3)stratego>!"foobar" "foobar"stratego>!Call(<id>, []) Call("foobar", [])stratego>mod2 = <mod>(<id>,2)stratego>!6 6stratego>mod2 0
As should now be a common pattern, term projects are implemented by
translation to a combination of match and build expressions.
Thus, a term wrap !p[<s>] is translated to a strategy
expression
{x: where(s => x); !p[x]}
where x is a fresh variable not occurring in
s.
In other words, the strategy s is applied to the
current subject term, i.e., the term to which
the build is applied.
As an example, the term wrap !Foo(Bar(<id>)) is
desugared to the strategy
\{x: where(id => x); !Foo(Bar(x))}
which after simplification is equivalent to \{x: ?x;
!Foo(Bar(x))\}, i.e., exactly the original lambda rule
\ x -> Foo(Bar(x))\.
Term projections are the match dual of term wraps.
Term projections can be used to project a
subterm from a term pattern. For example, the expression
?And(<id>,x) matches terms of the form
And(t1,t2) and reduces them to the first subterm
t1.
Another example is the strategy
map(?FunDec(<id>,_,_))
which reduces a list of function declarations to a list of the
names of the functions, i.e., the first arguments of the
FunDec constructor.
Here are some more examples:
[1,2,3]stratego>?[_|<id>] [2,3]stratego>!Call("foobar", []) Call("foobar", [])stratego>?Call(<id>, []) "foobar"
Term projections can also be used to apply additional constraints
to subterms in a match pattern. For example, ?Call(x,
<?args; length => 3>) matches only with function calls
with three arguments.
A match expression ?p[<s>] is desugared as
{x: ?p[x]; <s> x}
That is, after the pattern p[x] matches, it is reduced
to the subterm bound to x to which s is
applied. The result is also the result of the projection.
When multiple projects are used within a match the outcome is
undefined, i.e., the order in which the projects will be performed
can not be counted on.
Table of Contents
In Chapter 13 we saw a number of idioms of strategic rewriting, which all involved tree traversal. In the previous chapters we saw how strategies can be used to control transformations and how rules can be broken down into the primitive actions match, build and scope. The missing ingredient are combinators for defining traversals.
There are many ways to traverse a tree. For example, a bottom-up
traversal, visits the subterms of a node before it visits the node
itself, while a top-down traversal visits nodes before it visits
children. One-pass traversals traverse the tree one time, while
fixed-point traversals, such as innermost, repeatedly
traverse a term until a normal form is reached.
It is not desirable to provide built-in implementations for all traversals needed in transformations, since such a collection would necessarily be imcomplete. Rather we would like to define traversals in terms of the primitive ingredients of traversal. For example, a top-down, one-pass traversal strategy will first visit a node, and then descend to the children of a node in order to recursively traverse all subterms. Similarly, the bottom-up, fixed-point traversal strategy innermost, will first descend to the children of a node in order to recursively traverse all subterms, then visit the node itself, and possibly recursively reapply the strategy.
Traversal in Stratego is based on the observation that a full term traversal is a recursive closure of a one-step descent, that is, an operation that applies a strategy to one or more direct subterms of the subject term. By separating this one-step descent operator from recursion, and making it a first-class operation, many different traversals can be defined.
In this chapter we explore the ways in which Stratego supports the definition of traversal strategies. We start with explicitly programmed traversals using recursive traversal rules. Next, congruences operators provide a more concise notation for such data-type specific traversal rules. Finally, generic traversal operators support data type independent definitions of traversals, which can be reused for any data type. Given these basic mechanisms, we conclude with an an exploration of idioms for traversal and standard traversal strategies in the Stratego Library.
In Chapter 16 we saw
the following definition of the map strategy, which
applies a strategy to each element of a list:
map(s) : [] -> [] map(s) : [x | xs] -> [<s> x | <map(s)> xs]
The definition uses explicit recursive calls to the strategy in the
right-hand side of the second rule.
What map does is to traverse the
list in order to apply the argument strategy to all elements.
We can use the same technique to other term structures as well.
We will explore the definition of traversals using the propositional formulae from Chapter 13, where we introduced the following rewrite rules:
module prop-rules imports libstrategolib prop rules DefI : Impl(x, y) -> Or(Not(x), y) DefE : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) DN : Not(Not(x)) -> x DMA : Not(And(x, y)) -> Or(Not(x), Not(y)) DMO : Not(Or(x, y)) -> And(Not(x), Not(y)) DAOL : And(Or(x, y), z) -> Or(And(x, z), And(y, z)) DAOR : And(z, Or(x, y)) -> Or(And(z, x), And(z, y)) DOAL : Or(And(x, y), z) -> And(Or(x, z), Or(y, z)) DOAR : Or(z, And(x, y)) -> And(Or(z, x), Or(z, y))
In Chapter 13 we saw how a
functional style of rewriting could be encoded using extra
constructors. In Stratego we can achieve a similar approach by using
rule names, instead of extra constructors. Thus, one way to achieve
normalization to disjunctive normal form, is the use of an
explicitly programmed traversal, implemented using recursive rules,
similarly to the map example above:
module prop-dnf4 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules dnf : True -> True dnf : False -> False dnf : Atom(x) -> Atom(x) dnf : Not(x) -> <dnfred> Not (<dnf>x) dnf : And(x, y) -> <dnfred> And (<dnf>x, <dnf>y) dnf : Or(x, y) -> Or (<dnf>x, <dnf>y) dnf : Impl(x, y) -> <dnfred> Impl(<dnf>x, <dnf>y) dnf : Eq(x, y) -> <dnfred> Eq (<dnf>x, <dnf>y) strategies dnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)
The dnf rules recursively apply themselves to the
direct subterms and then apply dnfred to actually apply
the rewrite rules.
We can reduce this program by abstracting over the base cases. Since
there is no traversal into True, False,
and Atoms, these rules can be be left out.
module prop-dnf5 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules dnft : Not(x) -> <dnfred> Not (<dnf>x) dnft : And(x, y) -> <dnfred> And (<dnf>x, <dnf>y) dnft : Or(x, y) -> Or (<dnf>x, <dnf>y) dnft : Impl(x, y) -> <dnfred> Impl(<dnf>x, <dnf>y) dnft : Eq(x, y) -> <dnfred> Eq (<dnf>x, <dnf>y) strategies dnf = try(dnft) dnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)
The dnf strategy is now defined in terms of the
dnft rules, which implement traversal over the
constructors. By using try(dnft), terms for which no
traversal rule has been specified are not transformed.
We can further simplify the definition by observing that the
application of dnfred does not necessarily have to take
place in the right-hand side of the traversal rules.
module prop-dnf6 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules dnft : Not(x) -> Not (<dnf>x) dnft : And(x, y) -> And (<dnf>x, <dnf>y) dnft : Or(x, y) -> Or (<dnf>x, <dnf>y) dnft : Impl(x, y) -> Impl(<dnf>x, <dnf>y) dnft : Eq(x, y) -> Eq (<dnf>x, <dnf>y) strategies dnf = try(dnft); dnfred dnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)
In this program dnf first calls dnft to
transform the subterms of the subject term, and then calls
dnfred to apply the transformation rules (and possibly
a recursive invocation of dnf).
The program above has two problems. First, the traversal behaviour
is mostly uniform, so we would like to specify that more
concisely. We will address that concern below. Second, the traversal
is not reusable, for example, to define a conjunctive normal form
transformation. This last concern can be addressed by factoring out
the recursive call to dnf and making it a parameter of
the traversal rules.
module prop-dnf7 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules proptr(s) : Not(x) -> Not (<s>x) proptr(s) : And(x, y) -> And (<s>x, <s>y) proptr(s) : Or(x, y) -> Or (<s>x, <s>y) proptr(s) : Impl(x, y) -> Impl(<s>x, <s>y) proptr(s) : Eq(x, y) -> Eq (<s>x, <s>y) strategies dnf = try(proptr(dnf)); dnfred dnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf) cnf = try(proptr(cnf)); cnfred cnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR); cnf)
Now the traversal rules are reusable and used in two different
transformations, by instantiation with a call to the particular
strategy in which they are used (dnf or
cnf).
But we can do better, and also make the composition of this strategy reusable.
module prop-dnf8 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules proptr(s) : Not(x) -> Not (<s>x) proptr(s) : And(x, y) -> And (<s>x, <s>y) proptr(s) : Or(x, y) -> Or (<s>x, <s>y) proptr(s) : Impl(x, y) -> Impl(<s>x, <s>y) proptr(s) : Eq(x, y) -> Eq (<s>x, <s>y) strategies propbu(s) = proptr(propbu(s)); s strategies dnf = propbu(dnfred) dnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf) cnf = propbu(cnfred) cnfred = try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR); cnf)
That is, the propbu(s) strategy defines a complete
bottom-up traversal over propostion terms, applying the strategy
s to a term after transforming its subterms. The
strategy is completely independent of the dnf and
cnf transformations, which instantiate the strategy
using the dnfred and cnfred strategies.
Come to think of it, dnfred and cnfred are
somewhat useless now and can be inlined directly in the
instantiation of the propbu(s) strategy:
module prop-dnf9 imports libstrategolib prop-rules strategies main = io-wrap(dnf) rules proptr(s) : Not(x) -> Not (<s>x) proptr(s) : And(x, y) -> And (<s>x, <s>y) proptr(s) : Or(x, y) -> Or (<s>x, <s>y) proptr(s) : Impl(x, y) -> Impl(<s>x, <s>y) proptr(s) : Eq(x, y) -> Eq (<s>x, <s>y) strategies propbu(s) = proptr(propbu(s)); s strategies dnf = propbu(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)) cnf = propbu(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR); cnf))
Now we have defined a transformation independent traversal strategy that is specific for proposition terms.
Next we consider cheaper ways for defining the traversal rules, and then ways to get completely rid of them.
The definition of the traversal rules above frequently occurs in the
definition of transformation strategies.
Congruence operators provide a convenient abbreviation of precisely
this operation.
A congruence operator applies a strategy to each direct subterm of a
specific constructor.
For each n-ary constructor c declared in a signature, there is a
corresponding congruence operator c(s1 ,
..., sn), which applies to terms of the form c(t1 ,
..., tn) by applying the argument strategies to the
corresponding argument terms.
A congruence fails if the application of one the argument strategies
fails or if constructor of the operator and that of the term do not
match.
Example. For example, consider the following signature of expressions:
module expressions
signature
sorts Exp
constructors
Int : String -> Exp
Var : String -> Exp
Plus : Exp * Exp -> Exp
Times : Exp * Exp -> Exp
The following Stratego Shell session applies the congruence
operators Plus and Times to a term:
stratego>import expressionsstratego>!Plus(Int("14"),Int("3")) Plus(Int("14"),Int("3"))stratego>Plus(!Var("a"), id) Plus(Var("a"),Int("3"))stratego>Times(id, !Int("42")) command failed
The first application shows how a congruence transforms a specific subterm, that is the strategy applied can be different for each subterm. The second application shows that a congruence only succeeds for terms constructed with the same constructor.
The import at the start of the session is necessary to
declare the constructors used; the definitions of congruences are
derived from constructor declarations.
Forgetting this import would lead to a complaint about an undeclared
operator:
stratego>!Plus(Int("14"),Int("3")) Plus(Int("14"),Int("3"))stratego>Plus(!Var("a"), id) operator Plus/(2,0) not defined command failed
Defining Traversals with Congruences.
Now we return to our dnf/cnf example, to
see how congruence operators can help in their implementation.
Since congruence operators basically define a one-step traversal for
a specific constructor, they capture the traversal rules defined above.
That is, a traversal rule such as
proptr(s) : And(x, y) -> And(<s>x, <s>y)
can be written by the congruence And(s,s).
Applying this to the prop-dnf program we can replace
the traversal rules by congruences as follows:
module prop-dnf10 imports libstrategolib prop-rules strategies main = io-wrap(dnf) strategies proptr(s) = Not(s) <+ And(s, s) <+ Or(s, s) <+ Impl(s, s) <+ Eq(s, s) propbu(s) = proptr(propbu(s)); s strategies dnf = propbu(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)) cnf = propbu(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR); cnf))
Observe how the five traversal rules have been reduced to five congruences which fit on a single line.
Traversing Tuples and Lists.
Congruences can also be applied to tuples,
(s1,s2,...,sn), and lists,
[s1,s2,...,sn]. A special list congruence is
[] which 'visits' the empty list.
As an example, consider again the definition of map(s)
using recursive traversal rules:
map(s) : [] -> [] map(s) : [x | xs] -> [<s> x | <map(s)> xs]
Using list congruences we can define this strategy as:
map(s) = [] <+ [s | map(s)]
The [] congruence matches an empty list. The [s |
map(s)] congruence matches a non-empty list, and applies
s to the head of the list and map(s) to
the tail. Thus, map(s) applies s to each
element of a list:
stratego>import liblibstratego>![1,2,3] [1,2,3]stratego>map(inc) [2,3,4]
Note that map(s) only succeeds if s
succeeds for each element of the list.
The fetch and filter strategies are
variations on map that use the failure of
s to list elements.
fetch(s) = [s | id] <+ [id | fetch(s)]
The fetch strategy traverses a list
until it finds a element for which
s succeeds and then stops. That element is the only one
that is transformed.
filter(s) = [] + ([s | filter(s)] <+ ?[ |<id>]; filter(s))
The filter strategy applies s to each
element of a list, but only keeps the elements for which it
succeeds.
stratego>import liblibstratego>even = where(<eq>(<mod>(<id>,2),0))stratego>![1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8]stratego>filter(even) [2,4,6,8]
Format Checking. Another application of congruences is in the definition of format checkers. A format checker describes a subset of a term language using a recursive pattern. This can be used to verify input or output of a transformation, and for documentation purposes. Format checkers defined with congruences can check subsets of signatures or regular tree grammars. For example, the subset of terms of a signature in a some normal form.
As an example, consider checking the output of the dnf
and cnf transformations.
conj(s) = And(conj(s), conj(s)) <+ s disj(s) = Or (disj(s), disj(s)) <+ s // Conjunctive normal form conj-nf = conj(disj(Not(Atom(x)) <+ Atom(x))) // Disjunctive normal form disj-nf = disj(conj(Not(Atom(x)) <+ Atom(x)))
The strategies conj(s) and disj(s) check
that the subject term is a conjunct or a disjunct, respectively,
with terms satisfying s at the leaves.
The strategies conj-nf and disj-nf check
that the subject term is in conjunctive or disjunctive normal form,
respectively.
Using congruence operators we constructed a generic,
i.e. transformation independent, bottom-up traversal for proposition
terms. The same can be done for other data types. However, since the
sets of constructors of abstract syntax trees of typical programming
languages can be quite large, this may still amount to quite a bit
of work that is not reusable across data types;
even though a strategy such as `bottom-up traversal', is basically
data-type independent.
Thus, Stratego provides generic traversal by means of several
generic one-step descent operators. The
operator all, applies a strategy to all direct
subterms. The operator one, applies a strategy to one
direct subterm, and the operator some, applies a
strategy to as many direct subterms as possible, and at least one.
The all(s) strategy transforms a constructor
application by applying the parameter strategy s to
each direct subterm. An application of all(s) fails if
the application to one of the subterms fails.
The following example shows how all (1) applies to any
term, and (2) applies its argument strategy uniformly to all direct
subterms. That is, it is not possible to do something special for a
particular subterm (that's what congruences are for).
stratego>!Plus(Int("14"),Int("3")) Plus(Int("14"),Int("3"))stratego>all(!Var("a")) Plus(Var("a"),Var("a"))stratego>!Times(Var("b"),Int("3")) Times(Var("b"),Int("3"))stratego>all(!Var("z")) Times(Var("z"),Var("z"))
The all(s) operator is really the ultimate replacement
for the traversal rules that we saw above. Instead of specifying a
rule or congruence for each constructor, the single application of
the all operator takes care of traversing all
constructors.
Thus, we can replace the propbu strategy by a
completely generic definition of bottom-up traversal. Consider again
the last definition of propbu:
proptr(s) = Not(s) <+ And(s, s) <+ Or(s, s) <+ Impl(s, s) <+ Eq(s, s) propbu(s) = proptr(propbu(s)); s
The role of proptr(s) in this definition can be
replaced by all(s), since that achieves exactly the
same, namely applying s to the direct subterms of
constructors:
propbu(s) = all(propbu(s)); s
However, the strategy now is completely generic, i.e. independent of
the particular structure it is applied to. In the Stratego Library
this strategy is called bottomup(s), and defined as
follows:
bottomup(s) = all(bottomup(s)); s
It first recursively transforms the subterms of the subject term and
then applies s to the result.
Using this definition, the normalization of propositions now reduces
to the following module, which is only concerned with the selection
and composition of rewrite rules:
module prop-dnf11 imports libstrategolib prop-rules strategies main = io-wrap(dnf) strategies dnf = bottomup(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR); dnf)) cnf = bottomup(try(DN <+ (DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR); cnf))
In fact, these definitions still contain a reusable pattern. With a little squinting we see that the definitions match the following pattern:
dnf = bottomup(try(dnf-rules; dnf)) cnf = bottomup(try(cnf-rules; cnf))
In which we can recognize the definition of innermost reduction, which the Stratego Library defines as:
innermost(s) = bottomup(try(s; innermost(s)))
The innermost strategy performs a bottom-up traversal
of a term. After transforming the subterms of a term it tries to
apply the transformation s. If succesful the result is
recursively transformed with an application of
innermost.
This brings us to the final form for the proposition normalizations:
module prop-dnf12 imports libstrategolib prop-rules strategies main = io-wrap(dnf) strategies dnf = innermost(DN <+ DefI <+ DefE <+ DMA <+ DMO <+ DAOL <+ DAOR) cnf = innermost(DN <+ DefI <+ DefE <+ DMA <+ DMO <+ DOAL <+ DOAR)
Different transformations can be achieved by using a selection of rules and a strategy, which is generic, yet defined in Stratego itself using strategy combinators.
The one(s) strategy transforms a constructor
application by applying the parameter strategy s to
exactly one direct subterm. An application of one(s)
fails if the application to all of the subterms fails.
The following Stratego Shell session illustrates the behaviour of
the combinator:
stratego>!Plus(Int("14"),Int("3")) Plus(Int("14"),Int("3"))stratego>one(!Var("a")) Plus(Var("a"),Int("3"))stratego>one(\ Int(x) -> Int(<addS>(x,"1")) \ ) Plus(Var("a"),Int("4"))stratego>one(?Plus(_,_)) command failed
A frequently used application of one is the
oncetd(s) traversal, which performs a left to right
depth first search/transformation that stops as soon as
s has been successfuly applied.
oncetd(s) = s <+ one(oncetd(s))
Thus, s is first applied to the root of the subject
term. If that fails, its direct subterms are searched one by one
(from left to right), with a recursive call to
oncetd(s).
An application of oncetd is the
contains(|t) strategy, which checks whether the subject
term contains a subterm that is equal to t.
contains(|t) = oncetd(?t)
Through the depth first search of oncetd, either an
occurrence of t is found, or all subterms are verified
to be unequal to t.
Here are some other one-pass traversals using the one
combinator:
oncebu(s) = one(oncebu(s)) <+ s spinetd(s) = s; try(one(spinetd(s))) spinebu(s) = try(one(spinebu(s))); s
Exercise: figure out what these strategies do.
Here are some fixe-point traversals, i.e., traversals that apply their argument transformation exhaustively to the subject term.
reduce(s) = repeat(rec x(one(x) + s)) outermost(s) = repeat(oncetd(s)) innermostI(s) = repeat(oncebu(s))
The difference is the subterm selection strategy. Exercise: create rewrite rules and terms that demonstrate the differences between these strategies.
The some(s) strategy transforms a constructor
application by applying the parameter strategy s to as
many direct subterms as possible and at least one. An application of
some(s) fails if the application to all of the subterms
fails.
Some one-pass traversals based on some:
sometd(s) = s <+ some(sometd(s)) somebu(s) = some(somebu(s)) <+ s
A fixed-point traversal with some:
reduce-par(s) = repeat(rec x(some(x) + s))
Above we have seen the basic mechanisms for defining traversals in Stratego: custom traversal rules, data-type specific congruence operators, and generic traversal operators. Term traversals can be categorized into classes according to how much of the term they traverse and to which parts of the term they modify. We will consider a number of idioms and standard strategies from the Stratego Library that are useful in the definition of traversals.
One class of traversal strategies performs a full
traversal, that is visits and transforms every subterm of
the subject term.
We already saw the bottomup strategy defined as
bottomup(s) = all(bottomup(s)); s
It first visits the subterms of the subject term, recursively
transforming its subterms, and then applies the
transformation s to the result.
A related strategy is topdown, which is defined as
topdown(s) = s; all(topdown(s))
It first transforms the subject therm and then visits the subterms of the result.
A combination of topdown and bottomup is
downup, defined as
downup(s) = s; all(downup(s)); s
It applies s on the way down the tree, and again on the
way up.
A variation is downup(2,0)
downup(s1, s2) = s1; all(downup(s1, s2)); s2
which applies one strategy on the way down and another on the way up.
Since the parameter strategy is applied at every subterm, these
traversals only succeed if it succeeds everywhere. Therefore, these
traversals are typically applied in combination with
try or repeat.
topdown(try(R1 <+ R2 <+ ...))
This has the effect that the rules are tried at each subterm. If none of the rules apply the term is left as it was and traversal continues with its subterms.
Choosing a Strategy. The strategy to be used for a particular transformation depends on the rules and the goal to be achieved.
For example, a constant folding transformation for proposition
formulae can be defined as a bottom-up traversal that tries to apply
one of the truth-rules T at each subterm:
T : And(True(), x) -> x T : And(x, True()) -> x T : And(False(), x) -> False() T : And(x, False()) -> False() T : Or(True(), x) -> True() T : Or(x, True()) -> True() T : Or(False(), x) -> x T : Or(x, False()) -> x T : Not(False()) -> True() T : Not(True()) -> False() eval = bottomup(try(T))
Bottomup is the strategy of choice here because it evaluates
subterms before attempting to rewrite a term.
An evaluation strategy using topdown
eval2 = topdown(try(T)) // bad strategy
does not work as well, since it attempts to rewrite terms before their subterms have been reduced, thus missing rewriting opportunities. The following Stratego Shell session illustrates this:
stratego>!And(True(), Not(Or(False(), True()))) And(True,Not(Or(False,True)))stratego>eval Falsestratego>!And(True(), Not(Or(False(), True()))) And(True,Not(Or(False,True)))stratego>eval2 Not(True)
Exercise: find other terms that show the difference between these strategies.
On the other hand, a desugaring transformation for propositions,
which defines implication and equivalence in terms of other
connectives is best defined as a topdown traversal
which tries to apply one of the rules DefI or
DefE at every subterm.
DefI : Impl(x, y) -> Or(Not(x), y) DefE : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) desugar = topdown(try(DefI <+ DefE))
Since DefE rewrites Eq terms to terms
involving Impl, a strategy with bottomup
does not work.
desugar2 = bottomup(try(DefI <+ DefE)) // bad strategy
Since the subterms of a node are traversed
before the node itself is visited, this
transformation misses the desugaring of the implications
(Impl) originating from the application of the
DefE rule.
The following Shell session illustrates this:
stratego>!Eq(Atom("p"), Atom("q")) Eq(Atom("p"),Atom("q"))stratego>desugar And(Or(Not(Atom("p")),Atom("q")),Or(Not(Atom("q")),Atom("p")))stratego>!Eq(Atom("p"), Atom("q")) Eq(Atom("p"),Atom("q"))stratego>desugar2 And(Impl(Atom("p"),Atom("q")),Impl(Atom("q"),Atom("p")))
Repeated Application.
In case one rule produces a term to which another desugaring rule
can be applied, the desugaring strategy should repeat the
application of rules to each subterm.
Consider the following rules and strategy for desugaring
propositional formulae to implicative normal form (using only
implication and False).
DefT : True() -> Impl(False(), False()) DefN : Not(x) -> Impl(x, False()) DefA2 : And(x, y) -> Not(Impl(x, Not(y))) DefO1 : Or(x, y) -> Impl(Not(x), y) DefE : Eq(x, y) -> And(Impl(x, y), Impl(y, x)) impl-nf = topdown(repeat(DefT <+ DefN <+ DefA2 <+ DefO1 <+ DefE))
Application of the rules with try instead of
repeat
impl-nf2 = topdown(try(DefT <+ DefN <+ DefA2 <+ DefO1 <+ DefE)) // bad strategy
is not sufficient, as shown by the following Shell session:
stratego>!And(Atom("p"),Atom("q")) And(Atom("p"),Atom("q"))stratego>impl-nf Impl(Impl(Atom("p"),Impl(Atom("q"),False)),False)stratego>!And(Atom("p"),Atom("q")) And(Atom("p"),Atom("q"))stratego>impl-nf2 Not(Impl(Atom("p"),Impl(Atom("q"),False)))
Note that the Not is not desugared with
impl-nf2.
Paramorphism. A variation on bottomup is a traversal that also provides the original term as well as the term in which the direct subterms have been transformed. (Also known as a paramorphism?)
bottomup-para(s) = <s>(<id>, <all(bottomup-para(s))>)
This is most useful in a bottom-up traversal; the original term is always available in a top-down traversal.
Exercise: give an example application of this strategy
Cascading transformations are transformations upon
transformations. While the full traversals discussed above walk over
the tree once, cascading transformations apply multiple `waves' of
transformations to the nodes in the tree.
The prototypical example is the innermost strategy,
which exhaustively applies a transformation, typically a set of
rules, to a tree.
simplify = innermost(R1 <+ ... <+ Rn)
The basis of innermost is a bottomup
traversal that tries to apply the transformation at each node after
visiting its subterms.
innermost(s) = bottomup(try(s; innermost(s)))
If the transformation s succeeds, the result term is
transformed again with a recursive call to innermost.
Application of innermost exhaustively applies
one set of rules to a tree.
Using sequential composition we can apply several
stages of reductions.
A special case of such a staged transformation,
is known as sequence of normal forms (in the
TAMPR system):
simplify = innermost(A1 <+ ... <+ Ak) ; innermost(B1 <+ ... <+ Bl) ; ... ; innermost(C1 <+ ... <+ Cm)
At each stage the term is reduced with respect to a different set of rules.
Of course it is possible to mix different types of transformations in such a stage pipeline, for example.
simplify = topdown(try(A1 <+ ... <+ Ak)) ; innermost(B1 <+ ... <+ Bl) ; ... ; bottomup(repeat(C1 <+ ... <+ Cm))
At each stage a different strategy and different set of rules can be used. (Of course one may use the same strategy several times, and some of the rule sets may overlap.)
While completely generic strategies such as bottomup
and innermost are often useful, there are also
situations where a mixture of generic and data-type specific
traversal is necessary. Fortunately, Stratego allows you to mix
generic traversal operators, congruences, your own traversal and
regular rules, any way you see fit.
A typical pattern for such strategies first tries a number of special cases that deal with traversal themselves. If none of the special cases apply, a generic traversal is used, followed by application of some rules applicable in the general case.
transformation = special-case1 <+ special-case2 <+ special-case3 <+ all(transformation); reduce reduce = ...
Constant Propagation. A typical example is the following constant propagation strategy. It uses the exceptions to the basic generic traversal to traverse the tree in the order of the control-flow of the program that is represented by the term. This program makes use of dynamic rewrite rules, which are used to propagate context-sensitive information through a program. In this case, the context-sensitive information concerns the constant values of some variables in the program, which should be propagated to the uses of those variables. Dynamic rules will be explained in Chapter 20; for now we are mainly concerned with the traversal strategy.
module propconst
imports
liblib
signature
constructors
Var : String -> Exp
Plus : Exp * Exp -> Exp
Assign : String * Exp -> Stat
If : Exp * Stat * Stat -> Stat
While : Exp * Stat -> Stat
strategies
propconst =  PropConst
PropConst  <+ propconst-assign
<+ propconst-if
<+ propconst-while
<+ all(propconst); try(EvalBinOp)
EvalBinOp :
<+ propconst-assign
<+ propconst-if
<+ propconst-while
<+ all(propconst); try(EvalBinOp)
EvalBinOp :  Plus(Int(i), Int(j)) -> Int(k) where <addS>(i,j) => k
EvalIf :
If(Int("0"), s1, s2) -> s2
EvalIf :
If(Int(i), s1, s2) -> s1 where <not(eq)>(i, "0")
propconst-assign =
Plus(Int(i), Int(j)) -> Int(k) where <addS>(i,j) => k
EvalIf :
If(Int("0"), s1, s2) -> s2
EvalIf :
If(Int(i), s1, s2) -> s1 where <not(eq)>(i, "0")
propconst-assign =  Assign(?x, propconst => e)
; if <is-value> e then
rules( PropConst : Var(x) -> e )
else
rules( PropConst :- Var(x) )
end
propconst-if =
Assign(?x, propconst => e)
; if <is-value> e then
rules( PropConst : Var(x) -> e )
else
rules( PropConst :- Var(x) )
end
propconst-if =  If(propconst, id, id)
; (EvalIf; propconst
<+ (If(id, propconst, id) /PropConst\ If(id,id,propconst)))
propconst-while =
If(propconst, id, id)
; (EvalIf; propconst
<+ (If(id, propconst, id) /PropConst\ If(id,id,propconst)))
propconst-while =  While(id,id)
; (/PropConst\* While(propconst, propconst))
is-value = Int(id)
While(id,id)
; (/PropConst\* While(propconst, propconst))
is-value = Int(id)
The main strategy of the constant propagation transformation  , follows the pattern described
above; a number of special case alternatives followed by a generic
traversal alternative. The special cases are defined in their own
definitions.
Generic traversal is followed by the constant folding rule
, follows the pattern described
above; a number of special case alternatives followed by a generic
traversal alternative. The special cases are defined in their own
definitions.
Generic traversal is followed by the constant folding rule
EvalBinOp  .
.
The first special case is an application of the dynamic rule
PropConst, which replaces a constant valued variable by
its constant value  .
This rule is defined by the second special case strategy,
.
This rule is defined by the second special case strategy,
propconst-assign  . It first traverses the
right-hand side of an assignment with an
. It first traverses the
right-hand side of an assignment with an Assign
congruence operator, and a recursive call to
propconst. Then, if the expression evaluated to a
constant value, a new PropConst rule is
defined. Otherwise, any old instance of PropConst for
the left-hand side variable is undefined.
The third special case for If uses congruence operators
to order the application of propconst to its subterms
 . The first congruence
applies
. The first congruence
applies propconst to the condition expression. Then an
application of the rule EvalIf attempts to eliminate
one of the branches of the statement, in case the condition
evaluated to a constant value. If that is not possible the branches
are visited by two more congruence operator applications joined by a
dynamic rule intersection operator, which distributes the constant
propagation rules over the branches and merges the rules afterwards,
keeping only the consistent ones.
Something similar happens in the case of While
statements  .
For details concerning dynamic rules, see Chapter 20.
.
For details concerning dynamic rules, see Chapter 20.
To see what propconst achieves, consider the following
abstract syntax tree (say in file foo.prg).
Block([
Assign("x", Int("1")),
Assign("y", Int("42")),
Assign("z", Plus(Var("x"), Var("y"))),
If(Plux(Var("a"), Var("z")),
Assign("b", Plus(Var("x"), Int("1"))),
Block([
Assign("z", Int("17")),
Assign("b", Int("2"))
])),
Assign("c", Plus(Var("b"), Plus(Var("z"), Var("y"))))
])
We import the module in the Stratego Shell, read the abstract syntax
tree from file, and apply the propconst transformation
to it:
stratego>import libstrategolibstratego>import propconststratego><ReadFromFile> "foo.prg" ...stratego>propconst Block([Assign("x",Int("1")),Assign("y",Int("42")),Assign("z",Int("43")), If(Plux(Var("a"),Int("43")),Assign("b",Int("2")),Block([Assign("z", Int("17")),Assign("b",Int("2"))])),Assign("c",Plus(Int("2"),Plus( Var("z"),Int("42"))))])
Since the Stratego Shell does not (yet) pretty-print terms, the result is rather unreadable. We can remedy this by writing the result of the transformation to a file, and pretty-printing it on the regular command-line with pp-aterm.
stratego><ReadFromFile> "foo.prg" ...stratego>propconst; <WriteToTextFile> ("foo-pc.prg", <id>) ...stratego>:quit ...$pp-aterm -i foo-pc.prg Block( [ Assign("x", Int("1")) , Assign("y", Int("42")) , Assign("z", Int("43")) , If( Plux(Var("a"), Int("43")) , Assign("b", Int("2")) , Block( [Assign("z", Int("17")), Assign("b", Int("2"))] ) ) , Assign( "c" , Plus(Int("2"), Plus(Var("z"), Int("42"))) ) ] )
Compare the result to the original program and try to figure out what has happened and why that is correct. (Assuming the `usual' semantics for this type of imperative language.)
Generic Strategies with Exceptional Cases.
Patterns for mixing specific and generic traversal can be captured
in parameterized strategies such as the following. They are
parameterized with the usual transformation parameter s
and with a higher-order strategy operator stop, which
implements the special cases.
topdownS(s, stop: (a -> a) * b -> b) = rec x(s; (stop(x) <+ all(x))) bottomupS(s, stop: (a -> a) * b -> b) = rec x((stop(x) <+ all(x)); s) downupS(s, stop: (a -> a) * b -> b) = rec x(s; (stop(x) <+ all(x)); s) downupS(s1, s2, stop: (a -> a) * b -> b) = rec x(s1; (stop(x) <+ all(x)); s2)
While normal strategies (parameters) are functions from terms to
terms, the stop parameter is a function from strategies
to strategies. Such exceptions to the default have to be declared
explicitly using a type annotation.
Note that the bottomupS strategy is slightly different
from the pattern of the propconst strategy; instead of
applying s only after the generic
traversal case, it is here applied in all cases.
However, the added value of these strategies is not very high. The
payoff in the use of generic strategies is provided by the basic
generic traversal operators, which provide generic behaviour for all
constructors. The stop callback can make it harder to
understand the control-flow structure of a strategy; use with care
and don't overdo it.
Separate rules and strategies
While it is possible to construct your own strategies by mixing traversal elements and rules, in general, it is a good idea to try to get a clean separation between pure rewrite rules and a (simple) strategy that applies them.
The full traversals introduced above mostly visit all nodes in the tree. Now we consider traversals that visit only some of the nodes of a tree.
The oncet and oncebu strategies apply the
argument strategy s at one position in the tree. That
is, application is tried at every node along the traversal until it
succeeds.
oncetd(s) = s <+ one(oncetd(s)) oncebu(s) = one(oncebu(s)) <+ s
The sometd and somebu strategies are
variations on oncet and oncebu that apply
s at least once at some positions, but possibly many
times. As soon as one is found, searching is stopped, i.e., in the
top-down case searching in subtrees is stopped, in bottom-up case,
searching in upper spine is stopped.
sometd(s) = s <+ some(sometd(s)) somebu(s) = some(somebu(s)) <+ s
Similar strategies that find as many applications as possible, but at
least one, can be built using some:
manybu(s) = rec x(some(x); try(s) <+ s) manytd(s) = rec x(s; all(try(x)) <+ some(x))
somedownup(s) = rec x(s; all(x); try(s) <+ some(x); try(s))
The alltd(s) strategy stops as soon as it has found a
subterm to which s can be succesfully applied.
alltd(s) = s <+ all(alltd(s))
If s does not succeed, the strategy is applied
recursively at all direct subterms. This means that s
is applied along a frontier of the subject term. This strategy is
typically used in substitution operations in which subterms are
replaced by other terms. For example, the strategy
alltd(?Var(x); !e) replaces all occurrences of
Var(x) by e.
Note that alltd(try(s)) is not a useful strategy.
Since try(s) succeeds at the root of the term, no
traversal is done.
A typical application of alltd is the definition of
local transformations, that only apply to some specific subterm.
transformation =
alltd(
trigger-transformation
; innermost(A1 <+ ... <+ An)
)
Some relatives of alltd that add a strategy to apply on
the way up.
alldownup2(s1, s2) = rec x((s1 <+ all(x)); s2) alltd-fold(s1, s2) = rec x(s1 <+ all(x); s2)
Finally, the following strategies select the leaves of a tree, where the determination of what is a leaf is upto a parameter strategy.
leaves(s, is-leaf, skip: a * (a -> a) -> a) = rec x((is-leaf; s) <+ skip(x) <+ all(x)) leaves(s, is-leaf) = rec x((is-leaf; s) <+ all(x))
A spine of a term is a chain of nodes from the root to some
subterm. spinetd goes down one spine and applies
s along the way to each node on the spine. The
traversal stops when s fails for all children of a
node.
spinetd(s) = s; try(one(spinetd(s))) spinebu(s) = try(one(spinebu(s))); s spinetd'(s) = s; (one(spinetd'(s)) + all(fail)) spinebu'(s) = (one(spinebu'(s)) + all(fail)); s
Apply s everywhere along al spines where s
applies.
somespinetd(s) = rec x(s; try(some(x))) somespinebu(s) = rec x(try(some(x)); s) spinetd'(s) = rec x(s; (one(x) + all(fail))) spinebu'(s) = rec x((one(x) + all(fail)); s)
While these strategies define the notion of applying along a spine, they are rarely used. In practice one would use more specific traversals with that determine which subterm to include in the search for a path.
TODO: examples
TODO: format checking
TODO: matching of complex patterns
TODO: contextual rules (local traversal)
We have seen that tree traversals can be defined in several ways.
Recursive traversal rules allow finegrained specification of a
traversal, but usually require too much boilerplate code.
Congruence operators provide syntactic sugar for traversal rules
that apply a strategy to each direct subterm of a term.
The generic traversal operators all, one,
and some allow consise, data-type independent
implementation of traversals.
A host of traversal strategies can be obtained by a combination of
the strategy combinators from the previous chapters with these
traversal operators.
Table of Contents
In Chapter 17 we have seen combinators for composing type preserving strategies. That is, structural transformations in which basic transformation rules don't change the type of a term. Such strategies are typically applied in transformations, which change the structure of a term, but not its type. Examples are simplification and optimization. In this chapter we consider the class of type unifying strategies, in which terms of different types are mapped onto one type. The application area for this type of strategy is analysis of expresssions with examples such as free variables collection and call-graph extraction.
We consider the following example problems:
-
term-size: Count the number of nodes in a term
-
occurrences: Count number of occurrences of a subterm in a term
-
collect-vars: Collect all variables in expression
-
free-vars: Collect all free variables in expression
These problems have in common that they reduce a structure to a single value or to a collection of derived values. The structure of the original term is usually lost.
We start with examining these problems in the context of lists, and then generalize the solutions we find there to arbitrary terms using generic term deconstruction, which allows concise implementation of generic type unifying strategies, similarly to the generic traversal strategies of Chapter 17.
We start with considering type-unifying operations on lists.
Sum.
Reducing a list to a value can be conveniently expressed by means of
a fold, which has as parameters operations for reducing the list
constructors.
The foldr/2 strategy reduces a list by replacing each
Cons by an application of s2, and the
empty list by s1.
foldr(s1, s2) = []; s1 <+ \ [y|ys] -> <s2>(y, <foldr(s1, s2)> ys) \
Thus, when applied to a list with three terms the result is
<foldr(s1,s2)> [t1,t2,t3] => <s2>(t1, <s2>(t2, <s2>(t3, <s1> [])))
A typical application of foldr/2 is sum,
which reduces a list to the sum of its elements. It sums the
elements of a list of integers, using 0 for the empty
list and add to combine the head of a list and the
result of folding the tail.
sum = foldr(!0, add)
The effect of sum is illustrated by the following
application:
<foldr(!0,add)> [1,2,3] => <add>(1, <add>(2, <add>(3, <!0> []))) => 6
Note the build operator for replacing the empty list with
0; writing foldr(0, add) would be wrong,
since 0 by itself is a congruence operator, which
basically matches the subject term with the
term 0 (rather than replacing it).
Size.
The foldr/2 strategy does not touch the elements of a
list. The foldr/3 strategy is a combination of fold
and map that extends foldr/2 with a parameter that is
applied to the elements of the list.
foldr(s1, s2, f) = []; s1 <+ \ [y|ys] -> <s2>(<f>y, <foldr(s1,s2,f)>ys) \
Thus, when applying it to a list with three elements, we get:
<foldr(s1,s2)> [t1,t2,t3] => <s2>(<f>t1, <s2>(<f>t2, <s2>(<f>t3, <s1> [])))
Now we can solve our first example problem
term-size. The size of a list is its
length, which corresponds to the sum of the
list with the elements replaced by 1.
length = foldr(!0, add, !1)
Number of occurrences.
The number of occurrences in a list of terms that satisfy some
predicate, entails only counting those elements in the list for
which the predicate succeeds. (Where a predicate is implemented with
a strategy that succeeds only for the elements in the domain of the
predicate.)
This follows the same pattern as counting the length of a list, but
now only counting the elements for which s succeeds.
list-occurrences(s) = foldr(!0, add, s < !1 + !0)
Using list-occurrences and a match strategy we can
count the number of variables in a list:
list-occurrences(?Var(_))
Collect.
The next problem is to collect all terms for
which a strategy succeeds. We have already seen how to do this for
lists. The filter strategy reduces a list to the
elements for which its argument strategy succeeds.
filter(s) = [] <+ [s | filter(s)] <+ ?[ |<filter(s)>]
Collecting the variables in a list is a matter of filtering with the
?Var(_) match.
filter(?Var(_))
The final problem, collecting the free variables in a term, does not really have a counter part in lists, but we can mimick this if we consider having two lists; where the second list is the one with the bound variables that should be excluded.
(filter(?Var(_)),id); diff
This collects the variables in the first list and subtracts the variables in the second list.
We have seen how to do typical analysis transformations on lists. How can we generalize this to arbitrary terms? The general idea of a folding operator is that it replaces the constructors of a data-type by applying a function to combine the reduced arguments of constructor applications. For example, the following definition is a sketch for a fold over abstract syntax trees:
fold-exp(binop, assign, if, ...) = rec f( fold-binop(f, binop) <+ fold-assign(f, assign) <+ fold-if(f, if) <+ ... ) fold-binop(f, s) : BinOp(op, e1, e2) -> <s>(op, <f>e1, <f>e2) fold-assign(f, s) : Assign(e1, e2) -> <s>(<f>e1, <f>e2) fold-if(f, s) : If(e1, e2, e3) -> <s>(<f>e1, <f>e2, <f>e3)
For each constructor of the data-type the fold has an argument strategy and a rule that matches applications of the constructor, which it replaces with an application of the strategy to the tuple of subterms reduced by a recursive invocation of the fold.
Instantation of this strategy requires a rule for each constructor
of the data-type. For instance, the following instantiation defines
term-size using fold-exp by providing
rules that sum up the sizes of the subterms and add one
(inc) to account for the node itself.
term-size = fold-exp(BinOpSize, AssignSize, IfSize, ...) BinOpSize : (Plus(), e1, e2) -> <add; inc>(e1, e2) AssignSize : (e1, e2) -> <add; inc>(e1, e2) IfSize : (e1, e2, e3) -> <add; inc>(e1, <add>(e2, e3))
This looks suspiciously like the traversal rules in Chapter 17. Defining folds in this manner has several limitations. In the definition of fold, one parameter for each constructor is provided and traversal is defined explicitly for each constructor. Furthermore, in the instantiation of fold, one rule for each constructor is needed, and the default behaviour is not generically specified.
One solution would be to use the generic traversal strategy
bottomup to deal with fold:
fold-exp(s) = bottomup(s) term-size = fold-exp(BinOpSize <+ AssignSize <+ IfSize <+ ...) BinOpSize : BinOp(Plus(), e1, e2) -> <add>(1, <add>(e1, e2)) AssignSize : Assign(e1, e2) -> <add>(e1, e2) IfSize : If(e1, e2, e3) -> <add>(e1, <add>(e2, e3))
Although the recursive application to subterms is now defined generically , one still has to specify rules for the default behaviour.
Instead of having folding rules that are specific to a data type, such as
BinOpSize : BinOp(op, e1, e2) -> <add>(1, <add>(e1, e2)) AssignSize : Assign(e1, e2) -> <add>(1, <add>(e1, e2))
we would like to have a generic definition of the form
CSize : c(e1, e2, ...) -> <add>(e1, <add>(e2, ...))
This requires generic decomposition of a constructor application
into its constructor and the list with children. This can be done
using the # operator. The match strategy
?p1#(p2) decomposes a constructor application into its
constructor name and the list of direct subterms. Matching such a
pattern against a term of the form C(t1,...,tn) results
in a match of "C" against p1 and a match
of [t1,...,tn] against p2.
Plus(Int("1"), Var("2"))
stratego> ?c#(xs)
stratego> :binding c
variable c bound to "Plus"
stratego> :binding xs
variable xs bound to [Int("1"), Var("2")]
Crush.
Using generic term deconstruction we can now generalize the type
unifying operations on lists to arbitrary terms.
In analogy with the generic traversal operators we need a generic
one-level reduction operator.
The crush/3 strategy reduces a constructor application
by folding the list of its subterms using foldr/3.
crush(nul, sum, s) : c#(xs) -> <foldr(nul, sum, s)> xs
Thus, crush performs a fold-map over the direct
subterms of a term. The following application illustrates what
<crush(s1, s2, f)> C(t1, t2) => <s2>(<f>t1, <s2>(<f>t2, <s1>[]))
The following Shell session instantiates this application in two ways:
stratego>import libstrategolibstratego>!Plus(Int("1"), Var("2")) Plus(Int("1"),Var("2"))stratego>crush(id, id, id) (Int("1"),(Var("2"),[]))stratego>!Plus(Int("1"), Var("2")) Plus(Int("1"),Var("2"))stratego>crush(!Tail(<id>), !Sum(<Fst>,<Snd>), !Arg(<id>)) Sum(Arg(Int("1")),Sum(Arg(Var("2")),Tail([])))
The crush strategy is the tool we need to implement
solutions for the example problems above.
Size.
Counting the number of direct subterms of a term is similar to
counting the number of elements of a list. The definition of
node-size is the same as the definition of
length, except that it uses crush instead
of foldr:
node-size = crush(!0, add, !1)
Counting the number of subterms (nodes) in a term is a similar problem. But, instead of counting each direct subterm as 1, we need to count its subterms.
term-size = crush(!1, add, term-size)
The term-size strategy achieves this simply with a
recursive call to itself.
stratego><node-size> Plus(Int("1"), Var("2")) 2stratego><term-size> Plus(Int("1"), Var("2")) 5
Occurrences.
Counting the number of occurrences of a certain term in another
term, or more generally, counting the number of subterms that
satisfy some predicate is similar to counting the term size.
However, only those terms satisfying the predicate should be
counted.
The solution is again similar to the solution for lists, but now
using crush.
om-occurrences(s) = s < !1 + crush(!0, add, om-occurrences(s))
The om-occurrences strategy counts the
outermost subterms satisfying
s. That is, the strategy stops counting as soon as it
finds a subterm for which s succeeds.
The following strategy counts all occurrences:
occurrences(s) = <add>(<s < !1 + !0>, <crush(!0, add, occurrences(s))>)
It counts the current term if it satisfies s and adds
that to the occurrences in the subterms.
stratego><om-occurrences(?Int(_))> Plus(Int("1"), Plus(Int("34"), Var("2"))) 2stratego><om-occurrences(?Plus(_,_))> Plus(Int("1"), Plus(Int("34"), Var("2"))) 1stratego><occurrences(?Plus(_,_))> Plus(Int("1"), Plus(Int("34"), Var("2"))) 2
Collect.
Collecting the subterms that satisfy a
predicate is similar to counting, but now a
list of subterms is produced.
The collect(s) strategy collects all
outermost occurrences satisfying
s.
collect(s) = ![<s>] <+ crush(![], union, collect(s))
When encountering a subterm for which s succeeds, a
singleton list is produced. For other terms, the matching subterms
are collected for each direct subterm, and the resulting lists are
combined with union to remove duplicates.
A typical application of collect is the collection of
all variables in an expression, which can be defined as follows:
get-vars = collect(?Var(_))
Applying get-vars to an expression AST produces the
list of all subterms matching Var(_).
The collect-all(s) strategy collects
all occurrences satisfying s.
collect-all(s) = ![<s> | <crush(![], union, collect(s))>] <+ crush(![], union, collect(s))
If s succeeds for the subject term combines the subject
term with the collected terms from the subterms.
Free Variables. Collecting the variables in an expression is easy, as we saw above. However, when dealing with languages with variable bindings, a common operation is to extract only the free variables in an expression or block of statements. That is, the occurrences of variables that are not bound by a variable declaration. For example, in the expression
x + let var y := x + 1 in f(y, a + x + b) end
the free variables are {x, a, b}, but not
y, since it is bound by the declaration in the let.
Similarly, in the function definition
function f(x : int) = let var y := h(x) in x + g(z) * y end
the only free variable is z since x and
y are declared.
Here is a free variable extraction strategy for Tiger expressions.
It follows a similar pattern of mixing generic and data-type specific
operations as we saw in Chapter 17.
The crush alternative takes care of the non-special
constructors, while ExpVars and FreeVars
deal with the special cases, i.e. variables and variable binding
constructs:
free-vars = ExpVars <+ FreeVars(free-vars) <+ crush(![], union, free-vars) ExpVars : Var(x) -> [x] FreeVars(fv) : Let([VarDec(x, t, e1)], e2) -> <union>(<fv> e1, <diff>(<fv> e2, [x])) FreeVars(fv) : Let([FunctionDec(fdecs)], e2) -> <diff>(<union>(<fv> fdecs, <fv>e2), fs) where <map(?FunDec(<id>,_,_,_))> fdecs => fs FreeVars(fv) : FunDec(f, xs, t, e) -> <diff>(<fv>e, xs) where <map(Fst)> xs => xs
The FreeVars rules for binding constructs use their
fv parameter to recursively get the free variables from
subterms, and they subtract the bound variables from any free
variables found using diff.
We can even capture the pattern exhibited here in a generic collection algorithm with support for special cases:
collect-exc(base, special : (a -> b) * a -> b) = base <+ special(collect-exc(base, special)) <+ crush(![], union, collect-exc(base, special))
The special parameter is a strategy parameterized with
a recursive call to the collection strategy.
The original definition of free-vars above, can now be
replaced with
free-vars = collect-exc(ExpVars, FreeVars)
It can also be useful to construct terms
generically. For example, in parse tree implosion, application nodes
should be reduced to constructor applications. Hence build operators
can also use the # operator. In a strategy
!p1#(p2), the current subject term is replaced by a
constructor application, where the constructor name is provided by
p1 and the list of subterms by p2. So, if
p1 evaluates to "C" and p2
evaluates to [t1,...,tn], the expression
!p1#(p2) build the term C(t1,...,tn).
Imploding Parse Trees. A typical application of generic term construction is the implosion of parse trees to abstract syntax trees performed by implode-asfix. Parse trees produced by sglr have the form:
appl(prod(sorts, sort, attrs([cons("C")])),[t1,...,tn])
That is, a node in a parse tree consists of an encoding of the
original production from the syntax definition, and a list with
subtrees. The production includes a constructor annotation
cons("C") with the name of the abstract syntax tree
constructor. Such a tree node should be imploded to an abstract
syntax tree node of the form C(t1,...,tn).
Thus, this requires the construction of a term with constructor
C given the string with its name.
The following implosion strategy achieves this using generic term
construction:
implode = appl(id, map(implode)); Implode Implode : appl(prod(sorts, sort, attrs([cons(c)])), ts) -> c#(ts)
The Implode rule rewrites an appl term to
a constructor application, by extracing the constructor name from
the production and then using generic term construction to apply the
constructor.
Note that this is a gross over simplification of the actual implementation of implode-asfix. See the source code for the full strategy.
Generic term construction and deconstruction support the definition of generic analysis and generic translation problems. The generic solutions for the example problems term size, number of occurrences, and subterm collection demonstrate the general approach to solving these types of problems.
Table of Contents
Stratego programs can be used to analyze, generate, and transform object programs. In this process object programs are structured data represented by terms. Terms support the easy composition and decomposition of abstract syntax trees. For applications such as compilers, programming with abstract syntax is adequate; only small fragments, i.e., a few constructors per pattern, are manipulated at a time. Often, object programs are reduced to a core language that only contains the essential constructs. The abstract syntax can then be used as an intermediate language, such that multiple languages can be expressed in it, and meta-programs can be reused for several source languages.
However, there are many applications of program transformation in which the use of abstract syntax is not adequate since the distance between the concrete programs that we understand and the abstract syntax trees used in specifications is too large. Even with pattern matching on algebraic data types, the construction of large code fragments in a program generator can become painful. For example, even the following tiny program pattern is easier to read in the concrete variant
let d* in let var x ta := (e1*) in e2* end end
than the abstract variant
Let(d*, [Let([VarDec(x, ta, Seq(e1*))], e2*)])
While abstract syntax is manageable for fragments of this size (and sometimes even more concise!), it becomes unpleasant to use when larger fragments need to be specified.
Besides the problems of understandability and complexity, there are other reasons why the use of abstract syntax may be undesirable. Desugaring to a core language is not always possible. For example, in the renovation of legacy code the goal is to repair the bugs in a program, but leave it intact otherwise. This entails that a much larger abstract syntax needs to be dealt with. Another occasion that calls for the use of concrete syntax is the definition of transformation or generation rules by users (programmers) rather than by compiler writers (meta-programmers). Other application areas that require concrete syntax are application generation and structured document (XML) processing.
Hence, it is desirable to have a meta-language that lets us write object-program fragments in the concrete syntax of the object language. This requires the extension of the meta-language with the syntax of the object language of interest, such that expressions in that language are interpreted as terms. In this chapter it is shown how the Stratego language based on abstract syntax terms is extended to support the use of concrete object syntax for terms.
To appreciate the need for concrete syntax in program transformation, it is illuminating to constrast the use of concrete syntax with the traditional use of abstract syntax in a larger example. Program instrumentation is the extension of a program in a systematic way in order to obtain measurements during run-time. Instrumentation is used, for example, in debugging to get information about the run-time behaviour of a program, and in profiling to collect statistics about about run-time and call frequency of program elements. Here we consider a simple instrumentation scheme that instruments Tiger functions with calls to trace functions.
The following Stratego fragment shows rewrite rules that instrument
a function f such that it prints f entry
on entry of the function and f exit at the exit. The
actual printing is delegated to the functions enterfun
and exitfun. Functions are instrumented differently
than procedures, since the body of a function is an expression
statement and the return value is the value of the expression. It is
not possible to just glue a print statement or function call at the
end of the body. Therefore, a let expression is introduced, which
introduces a temporary variable to which the body expression of the
function is assigned. The code for the functions
enterfun and exitfun is generated by rule
IntroducePrinters. Note that the declarations of the
Let generated by that rule have been omitted.
instrument =
topdown(try(TraceProcedure + TraceFunction))
; IntroducePrinters
; simplify
TraceProcedure :
FunDec(f, x*, NoTp, e) ->
FunDec(f, x*, NoTp,
Seq([Call(Var("enterfun"),[String(f)]), e,
Call(Var("exitfun"),[String(f)])]))
TraceFunction :
FunDec(f, x*, Tp(tid), e) ->
FunDec(f, x*, Tp(tid),
Seq([Call(Var("enterfun"),[String(f)]),
Let([VarDec(x,Tp(tid),NilExp)],
[Assign(Var(x), e),
Call(Var("exitfun"),[String(f)]),
Var(x)])]))
IntroducePrinters :
e -> Let(..., e)
The next program program fragment implements the same instrumentation transformation, but now it uses concrete syntax.
TraceProcedure :
|[ function f(x*) = e ]| ->
|[ function f(x*) = (enterfun(s); e; exitfun(s)) ]|
where !f => s
TraceFunction :
|[ function f(x*) : tid = e ]| ->
|[ function f(x*) : tid =
(enterfun(s);
let var x : tid
in x := e; exitfun(s); x
end) ]|
where new => x ; !f => s
IntroducePrinters :
e -> |[ let var ind := 0
function enterfun(name : string) = (
ind := +(ind, 1);
for i := 2 to ind do print(" ");
print(name); print(" entry\\n"))
function exitfun(name : string) = (
for i := 2 to ind do print(" ");
ind := -(ind, 1);
print(name); print(" exit\\n"))
in e end ]|
It is clear that the concrete syntax version is much more concise
and easier to read. This is partly due to the fact that the concrete
version is shorter than the abstract version: 225 bytes vs 320 bytes
after eliminating all non-significant whitespace. However, the
concrete version does not use much fewer lines. A more important
reason for the increased understandability is that in order to read
the concrete version it is not necessary to mentally translate the
abstract syntax constructors into concrete ones. The implementation
of IntroducePrinters is only shown in concrete syntax
since its encoding in abstract syntax leads to unreadable code for
code fragments of this size.
Note that these rewrite rules cannot be applied as such using simple innermost rewriting. After instrumenting a function declaration, it is still a function declaration and can thus be instrumented again. Therefore, we use a single pass topdown strategy for applying the rules.
The example gives rise to several observations. The concrete syntax
version can be read without knowledge of the abstract syntax. On
the other hand, the abstract syntax version makes the tree structure
of the expressions explicit. The abstract syntax version is much
more verbose and is harder to read and write. Especially the
definition of large code fragments such as in rule
IntroducePrinters is unattractive in abstract syntax.
The abstract syntax version implements the concrete syntax version. The concrete syntax version has all properties of the abstract syntax version: pattern matching, term structure, can be traversed, etc.. In short, the concrete syntax is just syntactic sugar for the abstract syntax.
Extension of the Meta Language. The instrumentation rules make use of the concrete syntax of Tiger. However, program transformation should not be restricted to transformation of Tiger programs. Rather we would like to be able to handle arbitrary object languages. Thus, the object language or object languages that are used in a module should be a parameter to the compiler. The specification of instrumentation is based on the real syntax of Tiger, not on some combinators or infix expressions. This entails that the syntax of Stratego should be extended with the syntax of Tiger.
Meta-Variables. The patterns in the transformation rules are not just fragments of Tiger programs. Rather some elements of these fragments are considered as meta-variables. For example in the term
|[ function f(x*) = e ]|
the identifiers f, x*, and e
are not intended to be Tiger variables, but rather meta-variables,
i.e., variables at the level of the Stratego specification, ranging
over identifiers, lists of function arguments, and expresssions,
respectively.
Antiquotation.
Instead of indicating meta-variables implicitly we could opt for an
antiquotation mechanism that lets us splice in meta-level
expressions into a concrete syntax fragment. For example, using
~ and ~* as antiquotation operators, a
variant of rule TraceProcedure becomes:
TraceProcedure :
|[ function ~f(~* x*) = ~e ]| ->
|[ function ~f(~* x*) =
(enterfun(~String(f)); ~e; exitfun(~String(f))) ]|
With such antiquotation operators it becomes possible to directly embed meta-level computations that produce a piece of code within a syntax fragment.
In the previous section we have seen how the extension of Stratego with concrete syntax for terms improves the readability of meta-programs. In this section we describe the techniques used to achieve this extension.
To embed the syntax of an object language in the meta language the
syntax definitions of the two languages should be combined and the
object language sorts should be injected into the appropriate meta
language sorts. In the Stratego setting this is achieved as follows.
The syntax of a Stratego module m is declared in the
m.meta file, which declares the name of an SDF
module. For instance, for modules using Tiger concrete syntax, i.e.,
using the extension of Stratego with Tiger, the .meta
would contain
Meta([Syntax("StrategoTiger")])
thus declaring SDF module StrategoTiger.sdf as defining
the extension.
The SDF module combines the syntax of Stratego and the syntax of the object language(s) by importing the appropriate SDF modules. The syntax definition of Stratego is provided by the compiler. The syntax definition of the object language is provided by the user. For example, the following SDF module shows a fragment of the syntax of Stratego:
module Stratego-Terms
exports
context-free syntax
Int -> Term {cons("Int")}
String -> Term {cons("Str")}
Var -> Term {cons("Var")}
Id "(" {Term ","}* ")" -> Term {cons("Op")}
Term "->" Term -> Rule {cons("RuleNoCond")}
Term "->" Term "where" Strategy -> Rule {cons("Rule")}
The following SDF module StrategoTiger, defines
the extension of Stratego with Tiger as object language.
module StrategoTiger
imports Stratego [ Term => StrategoTerm
Var => StrategoVar
Id => StrategoId
StrChar => StrategoStrChar ]
imports Tiger Tiger-Variables
exports
context-free syntax
"|[" Dec "]|" -> StrategoTerm {cons("ToTerm"),prefer}
"|[" TypeDec "]|" -> StrategoTerm {cons("ToTerm"),prefer}
"|[" FunDec "]|" -> StrategoTerm {cons("ToTerm"),prefer}
"|[" Exp "]|" -> StrategoTerm {cons("ToTerm"),prefer}
"~" StrategoTerm -> Exp {cons("FromTerm"),prefer}
"~*" StrategoTerm -> {Exp ","}+ {cons("FromTerm")}
"~*" StrategoTerm -> {Exp ";"}+ {cons("FromTerm")}
"~int:" StrategoTerm -> IntConst {cons("FromTerm")}
The module illustrates several remarkable aspects of the embedding of object languages in meta languages using SDF.
A combined syntax definition is created by just importing appropriate syntax definitions. This is possible since SDF is a modular syntax definition formalism. This is a rather unique feature of SDF and essential to this kind of language extension. Since only the full class of context-free grammars, and not any of its subclasses such as LL or LR, are closed under composition, modularity of syntax definitions requires support from a generalized parsing technique. SDF2 employs scannerless generalized-LR parsing.
The syntax definitions for two languages may partially overlap,
e.g., define the same sorts. SDF2 supports renaming of sorts to
avoid name clashes and ambiguities resulting from them. In the
StrategoTiger module several sorts from the Stratego syntax
definition (Term, Id, Var,
and StrChar) are renamed since the Tiger definition
also defines these names. In practice, instead of doing this
renaming for each language extension, module
StrategoRenamed provides a syntax definition of
Stratego in which all sorts have been renamed.
The embedding of object language expressions in the meta-language is implemented by adding appropriate injections to the combined syntax definition. For example, the production
"|[" Exp "]|" -> StrategoTerm {cons("ToTerm"),prefer}
declares that a Tiger expression (Exp) between
|[ and ]| can be used everywhere where a
StrategoTerm can be used. Furthermore, abstract syntax
expressions (including meta-level computations) can be spliced into
concrete syntax expressions using the ~ splice
operators. To distinguish a term that should be interpreted as a
list from a term that should be interpreted as a list
element, the convention is to use a
~* operator for splicing a list.
The declaration of these injections can be automated by generating an appropriate production for each sort as a transformation on the SDF definition of the object language. It is, however, useful that the embedding can be programmed by the meta-programmer to have full control over the selection of the sorts to be injected, and the syntax used for the injections.
Using the injection of meta-language StrategoTerms into
object language Expressions it is possible to
distinguish meta-variables from object language identifiers. Thus,
in the term |[ var ~x := ~e]|, the expressions
~x and ~e indicate meta-level terms, and
hence x and e are meta-level variables.
However, it is attractive to write object patterns with as few squigles as possible. This can be achieved through another feature of SDF, i.e., variable declarations. The following SDF module declares syntax schemata for meta variables.
module Tiger-Variables
exports
variables
[s][0-9]* -> StrConst {prefer}
[xyzfgh][0-9]* -> Id {prefer}
[e][0-9]* -> Exp {prefer}
"ta"[0-9]* -> TypeAn {prefer}
"x"[0-9]* "*" -> {FArg ","}+ {prefer}
"d"[0-9]* "*" -> Dec+ {prefer}
"e"[0-9]* "*" -> {Exp ";"}+ {prefer}
According to this declaration x, y, and
g10 are meta-variables for identifiers and
e, e1, and e1023 are
meta-variables of sort Exp. The last three productions
declare variables over lists using the convention that these are
distinquished from other variables with an asterisk. Thus,
x* and x1* range over lists of function
arguments. The prefer attribute ensures that these identifiers are
preferred over normal Tiger identifiers.
Parsing a module according to the combined syntax and mapping the parse tree to abstract syntax results in an abstract syntax tree that contains a mixture of meta- and object-language abstract syntax. Since the meta-language compiler only deals with meta-language abstract syntax, the embedded object-language abstract syntax needs to be expressed in terms of meta abstract syntax. For example, parsing the following Stratego rule
|[ x := let d* in ~* e* end ]| -> |[ let d* in x := (~* e*) end ]|
with embedded Tiger expressions, results in the abstract syntax tree
Rule(ToTerm(Assign(Var(meta-var("x")),
Let(meta-var("d*"),FromTerm(Var("e*"))))),
ToTerm(Let(meta-var("d*"),
[Assign(Var(meta-var("x")),
Seq(FromTerm(Var("e*"))))])))
containing Tiger abstract syntax constructors (e.g.,
Let, Var, Assign) and
meta-variables (meta-var). The transition from meta
language to object language is marked by the ToTerm
constructor, while the transition from meta-language to
object-language is marked by the constructor FromTerm.
Such mixed abstract syntax trees can be normalized by `exploding' all embedded abstract syntax to meta-language abstract syntax. Thus, the above tree should be exploded to the following pure Stratego abstract syntax:
Rule(Op("Assign",[Op("Var",[Var("x")]),
Op("Let",[Var("d*"),Var("e*")])]),
Op("Let",[Var("d*"),
Op("Cons",[Op("Assign",[Op("Var",[Var("x")]),
Op("Seq",[Var("e*")])]),
Op("Nil",[])])]))
Observe that in this explosion all embedded constructor applications
have been translated to the form Op(C,[t1,...,tn]). For
example, the Tiger `variable' constructor Var(_)
becomes Op("Var",[_]), while the Stratego meta-variable
Var("e*") remains untouched, and meta-vars
become Stratego Vars. Also note how the list in the
second argument of the second Let is exploded to a
Cons/Nil list.
The resulting term corresponds to the abstract syntax for the rule
Assign(Var(x),Let(d*,e*)) -> Let(d*,[Assign(Var(x),Seq(e*))])
written with abstract syntax notations for terms.
The explosion of embedded abstract syntax does not depend on the
object language; it can be expressed generically, provided that
embeddings are indicated with the FromTerm
constructor.
Disambiguating Quotations. Sometimes the fragments used within quotations are too small for the parser to be able to disambiguate them. In those cases it is useful to have alternative versions of the quotation operators that make the sort of the fragment explicit. A useful, although somewhat verbose, convention is to use the sort of the fragment as operator:
"exp" "|[" Exp "]|" -> StrategoTerm {cons("ToTerm")}
Other Quotation Conventions.
The convention of using |[...]| and ~ as
quotation and anti-quotation delimiters is inspired by the notation
used in texts about semantics. It really depends on the application,
the languages involved, and the `audience' what kind of delimiters
are most appropriate.
The following notation was inspired by active web pages is
developed. For instance, the following quotation
%>...<% and antiquotation <%...%>
delimiters are defined for use of XML in Stratego programs:
context-free syntax
"%>" Content "<%" -> StrategoTerm {cons("ToTerm"),prefer}
"<%=" StrategoTerm "%>" -> Content {cons("FromTerm")}
"<%" StrategoStrategy "%>" -> Content {cons("FromApp")}
Desugaring Patterns. Some meta-programs first desugar a program before transforming it further. This reduces the number of constructs and shapes a program can have. For example, the Tiger binary operators are desugared to prefix form:
DefTimes : |[ e1 * e2 ]| -> |[ *(e1, e2) ]| DefPlus : |[ e1 + e2 ]| -> |[ +(e1, e2) ]|
or in abstract syntax
DefPlus : Plus(e1, e2) -> BinOp(PLUS, e1, e2)
This makes it easy to write generic transformations for binary operators. However, all subsequent transformations on binary operators should then be done on these prefix forms, instead of on the usual infix form. However, users/meta-programmers think in terms of the infix operators and would like to write rules such as
Simplify : |[ e + 0 ]| -> |[ e ]|
However, this rule will not match since the term to which it is applied has been desugared. Thus, it might be desirable to desugar embedded abstract syntax with the same rules with which programs are desugared. This phenomenon occurs in many forms ranging from removing parentheses and generalizing binary operators as above, to decorating abstract syntax trees with information resulting from static analysis such as type checking.
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
In the previous chapters we have shown how programmable rewriting strategies can provide control over the application of transformation rules, thus addresing the problems of confluence and termination of rewrite systems. Another problem of pure rewriting is the context-free nature of rewrite rules. A rule has access only to the term it is transforming. However, transformation problems are often context-sensitive. For example, when inlining a function at a call site, the call is replaced by the body of the function in which the actual parameters have been substituted for the formal parameters. This requires that the formal parameters and the body of the function are known at the call site, but these are only available higher-up in the syntax tree. There are many similar problems in program transformation, including bound variable renaming, typechecking, data flow transformations such as constant propagation, common-subexpression elimination, and dead code elimination. Although the basic transformations in all these applications can be expressed by means of rewrite rules, these require contextual information.
In Stratego context-sensitive rewriting can be achieved without the added complexity of local traversals and without complex data structures, by the extension of rewriting strategies with scoped dynamic rewrite rules. Dynamic rules are otherwise normal rewrite rules that are defined at run-time and that inherit information from their definition context. As an example, consider the following strategy definition as part of an inlining transformation:
DefineUnfoldCall =
?|[ function f(x) = e1 ]|
; rules(
UnfoldCall : |[ f(e2 ) ]| -> |[ let var x := e2 in e1 end ]|
)
The strategy DefineUnfoldCall matches a function
definition and defines the rewrite rule UnfoldCall,
which rewrites a call to the specific function f , as encountered in
the definition, to a let expression binding the formal parameter
x to the actual parameter e2 in the body
of the function e1 . Note that the variables
f, x , and e1 are bound in
the definition context of UnfoldCall. The
UnfoldCall rule thus defined at the function definition
site, can be used at all function call sites. The storage and
retrieval of the context information is handled transparently by the
underlying language implementation and is of no concern to the
programmer.
An overview with semantics and examples of dynamic rewrite rules in Stratego is available in the following publications:
-
M. Bravenboer, A. van Dam, K. Olmos, and E. Visser. Program Transformation with Scoped Dynamic Rewrite Rules. Fundamenta Informaticae, 69:1--56, 2005.
An extended version is available as technical report UU-CS-2005-005.
-
K. Olmos and E. Visser. Composing Source-to-Source Data-Flow Transformations with Rewriting Strategies and Dependent Dynamic Rewrite Rules. In R. Bodik, editor, 14th International Conference on Compiler Construction (CC'05), volume 3443 of Lecture Notes in Computer Science, pages 204--220. Springer-Verlag, April 2005.
An extended version is available as technical report UU-CS-2005-006
Since these publications provide a fairly complete and up-to-date picture of dynamic rules, incorporation into this manual is not as urgent as other parts of the language.
The Stratego Library was designed with one goal in mind: it should contain be a good collection of strategies, rules and data types for manipulating programs. In the previous part of this tutorial, we have already introduced you some of the specific features in the library for doing program manipulation. However, the library also contains abstract data types which are found in almost any library, such as lists, strings, hashtables, sets, file and console I/O, directory manipulation and more. In this chapter, we aim to complete your basic Stratego education by introducing you to how these bread-and-butter data types have been implemented for Stratego.
Online Library Documentation
Stratego and its library is a work in progress. New material is added to the library on a weekly basis. If you want to follow the progress, you should consult the latest version of the library documentation.
Beware that the online documentation will display strategies on the
form apply-and-fail(Strategy s, ATerm name, ATerm in-term, ATerm out),
whereas we adopt the more conventional format in this manual:
apply-and-fail(s | name, in-term, out)
The organization of the Stratego library is hierarchical. At the
coarsest level of organization, it is divided into packages, whose
named as on a path-like form, e.g.
collection/list. Each package in turn consists of one
or several modules. A module is a leaf in the hierarchy. It maps
to one Stratego (.str) file, and contains definitions
for strategies, rules, constructors and overlays. The available
packages in the library is listed below.
collection/hash-table collection/list collection/set collection/tuple lang strategy strategy/general strategy/pack strategy/traversal system/io system/posix term util util/config
As an example, the collection/list package consists of
the modules common, cons, filter,
index, integer, lookup,
set, sort, zip. Inside the
sort module, we find the qsort strategy,
for sorting lists.
In the remainder of this part of the tutorial, we will present the most important parts of the library, and show their typical usage patterns and idioms. If anything seems unclear, you are encouraged to consult the online documentation for further details.
Table of Contents
- 21. Arithmetic Operations
- 22. Lists
- 23. Strings
- 24. Hashtables and Sets
- 25. I/O
- 26. Command-line Options
- 27. Unit Testing with SUnit
- 28. Transformation Tool Composition with XTC
- 29. Building and Deploying Stratego Programs
- 30. Debugging Techniques for Stratego/XT
Table of Contents
In this chapter we introduce strategies for working with numbers. The Stratego runtime provides two kinds of numbers: real numbers and integers. They are both terms, but cannot be used interchangeably. The library strategies described in this chapter also maintain the distinction between real numbers and integers, but many may also be applied to strings which contain numbers.
Stratego does not have the normal mathematical syntax for
arithmetic operators, such as +, -,
/ and *. These operators are used for
other purposes. Instead, the library provides the operators
as the strategies, namely add, subt,
div and mul. Further, there is
convenience strategy for integer increment, inc
and decrement, dec.
While the Stratego language operates exclusively on terms, there
are different kinds of primitive terms. The runtime maintains a
distinction between real numbers and integer numbers. The library
mirrors this distinction by providing a family of strategies for
arithmetic operations. Arithmetic strategies which work on real
numbers end in an
r, e.g. addr, and strategies working on
integers end in an i, e.g. subti. For
each arithmetic operator, there is also a type-promoting variant,
e.g. mul, which will type-promote from integer to real,
when necessary. Finally, there are convenience strategies for
working on strings containing numbers. For each arithmetic operation,
there is a string variant, e.g divS.
The full set of arithmetic operations in Stratego:
add, addr, addi, addS div, divr, divi, divS mul, mulr, muli, mulS subt, subtr, subti, subtS
Using these strategies is straightforward.
stratego><addr> (1.5, 1.5) 3.000000000000000e+00stratego><subti> (5, 2) 3stratego><mul> (1.5, 2) 3.000000000000000e+00stratego><inc> 2 3
As we can see, the mul operator can be applied to a
pair which consists of different terms (real and integer). In
this case, type promotion from integer to real happens
automatically.
Working on Strings.
The string variants, e.g. addS and divS
work on strings containing integers. The result in strings
containing integers.
stratego><addS> ("40", "2") "42"stratego><divS> ("9", "3") "3"
The strategies found in the library for comparing two numbers correspond
to the usual mathematical operators for less-than (lt),
less-than-equal (leq), equal (eq),
greater-than (gt), greather-than-equal (geq).
As with the arithmetic strategies, each of these operators comes in
an integer variant, suffixed with i, a real variant
(suffixed by r), a string variant (suffixed by
S) and a type promoting variant without suffix. The
full matrix of comparison functions thus looks like:
lt, ltr, lti, ltS gt, gtr, gti, gtS leq, leqr, leqi, leqS geq, geqr, geqi, geqS
A few examples:
stratego><lt> (1.0, 2) (1.000000000000000e+00,2)stratego><ltS> ("1", "2") ("1", "2")stratego><geqS> ("2", "2") ("2","2")stratego><gtr> (0.9, 1.0) command failed
The maximum and minimum of a two-element tuple of numbers can be
found with the max and min strategies,
respectively. These do not distinguish between real and integers.
However, they do distinguish between numbers and strings;
maxS and minS are applicable to strings.
stratego><max> (0.9, 1.0) 1.0stratego><min> (99, 22) 22stratego><minS> ("99", "22") "22"
Some other properties of numbers, such as whether a number
is even, negative or positive, can be be tested with the strategies
even, neg and pos, respectively.
The modulus (remainder) of dividing an integer by another is
provided by the mod strategy. gcd gives
the greatest common divisor of two numbers. Both mod
and gcd work on a two-element tuple of integers. The
log2 strategy can be used to find the binary logarithm
of a number. It will only succeed if the provided number is an
integer and that number has an integer binary logarithm.
stratego><mod> (412,123) 43stratego><gcd> (412,123) 1stratego><log2> 16 4
The library provides a strategy for generating random numbers, called
next-random. The algorithm powering this random generator
requires an initial "seed" to be provided. This seed is just a
first random number. You can pick any integer you want, but it's
advisable to pick a different seed on each program execution. A popular
choice (though not actually random) is the number of seconds since epoch,
provided by time. The seed is initialized by the
set-random-seed strategy. The following code shows the
normal idiom for getting a random number in Stratego:
stratego>time ; set-random-seed []stratego>next-random 1543988747
The random number generator needs only be initialized with a seed once for every program invocation.
In this chapter, we saw that Stratego is different from many other
languages in that it does not provide the normal arithmetic operators.
We saw that instead, strategies such as add and
mul are used to add and multiply numbers. We also saw
which strategies to use for comparing numbers and generating random
numbers.
The module term/integer contains strategies for
working with numbers. Refer to the
library reference documentation
for more information.
Table of Contents
This chapter will introduce you to the basic strategies for working with lists. The strategies provide functionality for composing and decomposing, sorting, filtering, mering as well as constructing new abstractions from basic lists, such as associative lists.
Every value in Stratego is a term. This is also the case for lists.
You can write the list 1, 2, 3 as
Cons(1,Cons(2,Cons(3,Nil))), which is clearly a term.
Fortunately, Stratego also provides some convenient syntactic sugar
that makes lists more readable and easy to work with. We can write
the same list as [1,2,3], which will be desugared
internally in the the term above.
The most fundamental operations on lists is the ability
compose and decompose lists. In Stratego, list composition on
"sugared" lists, that is, lists writen in the sugared form,
has some sugar of its own. Assume xs is the list
[1,2,3]. The code [0|xs] will prepend a
0 to it, yielding [0,1,2,3]. List decomposition is done using
the match operator. The code ![0,1,2,3] ; ?[y|ys]
will bind y to the head of the list, 0,
and ys to the tail of the list, [1,2,3].
The module collection/list contains a lot of convenience
functions for dealing with lists. (collection/list is
contained in the liblib library.) For example, the strategy
elem will check if a given value is in a list. If it
is, the identity of the list will be returned.
stratego>import liblibstratego><elem> (1, [2,3,1,4]) [2,3,1,4]
Continuing on the above Stratego Shell session, we can exercise some of the other strategies:
stratego><length> [1,2,3,4,5] 5stratego><last> [5,6,7,8,9] 9stratego><reverse> [1,2,3,4,5] [5,4,3,2,1]
There are two strategies for concatenating lists. If the lists
are given as a tuple, use conc. If you have a list
of lists, use concat:
stratego><conc> ([1,2,3],[4,5,6],[7,8,9]) [1,2,3,4,5,6,7,8,9]stratego><concat> [[1,2,3],[4,5,6],[7,8,9]] [1,2,3,4,5,6,7,8,9]
The sublist of the first n elements can be
picked out with the take(|n) strategy:
stratego> <take(|3)> [1,2,3,4,5]
[1,2,3]
Finally, the fetch(s) strategy can be used to find
the first element for which s succeeds:
stratego> <fetch(?2)> [1,2,3]
2
The Stratego library contains many other convenient functions, which are documented in the API documentation.
The list sorting function is called qsort(s), and
implements the Quicksort algorithm. The strategy parameter
s is the comparator function.
stratego> <qsort(gt)> [2,3,5,1,9,7]
[9,7,5,3,2,1]
Stratego also has library support for associative lists, sometimes known
as assoc lists. There are essentially lists of (key, value)
pairs, and work like a poor man's hash table. The primary strategy for
working with these lists is lookup. This strategy looks up
the first value associated with a particular key, and returns it.
stratego> <lookup> (2, [(1, "a"), (2, "b"), (3, "c")]) => "b"
The library also contains some useful strategies for
combining multiple lists. The cart(s) strategy
makes a cartesian product of two lists. For each pair,
the parameter strategy s will be called. In
the second case below, each pair will be summed by
add.
stratego><cart(id)> ([1,2,3],[4,5,6]) [(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6)]stratego><cart(add)> ([1,2,3],[4,5,6]) [5,6,7,6,7,8,7,8,9]
Two lists can be paired using zip(s). It takes
a tuple of two lists, and will successively pick out the head
of the lists and pair them into a tuple, and apply
s to the tuple. zip is equivalent
to zip(id).
stratego><zip> ([1,2,3],[4,5,6]) [(1,4),(2,5),(3,6)]stratego><zip(add)> ([1,2,3],[4,5,6]) [5,6,7]
The inverse function of zip is unzip.
stratego> <unzip> [(1,4),(2,5),(3,6)]
([1,2,3],[4,5,6])
There is also unzip(s) which like unzip
takes a list of two-element tuples , and applies s
to each tuple before unzipping them into two lists.
In Stratego, lightweight sets are implemented as lists. A set differs
from a list in that a given element (value) can only occur once. The
strategy nub (also known as make-set)
can be use to make a list into a set. It will remove duplicate
elements. The normal functions on sets are provided, among
them union, intersection, difference and equality:
stratego><nub> [1,1,2,2,3,4,5,6,6] [1,2,3,4,5,6]stratego><union> ([1,2,3],[3,4,5]) [1,2,3,4,5]stratego><diff> ([1,2,3],[3,4,5]) [1,2]stratego><isect> ([1,2,3],[3,4,5]) [3]stratego><set-eq> ([1,2,3],[1,2,3]) ([1,2,3],[1,2,3])
Elementwise transformation of a list is normally done with the
map(s) strategy. It must be applied to a list.
When used, it will apply the strategy s to each
element in the list, as shown here. It will return a list of equal
length to the input. If the application of s fails
on one of the elements map(s) fails.
stratego> <map(inc)> [1,2,3,4]
[2,3,4,5]
mapconcat(s) is another variant of the
elementwise strategy application, equivalent to
map(s) ; concat. It takes a strategy
s which will be applied to each element.
The strategy s must always result in a list,
thus giving a list of lists, which will be concatenated.
A slightly more convoluted version of the above mapping.
If we want to remove
elements from the list, we can use filter(s).
The filter strategy will apply s
to each element of a list, and keep whichever elements
it succeeds on:
stratego> <filter(?2 ; !6)> [1,2,3,2]
[6,6]
stratego> <mapconcat(\ x -> [ <inc> x ] \)> [1,2,3,4]
List folding is a somewhat flexible technique primarily intended
for reducing a list of elements to a single value. Think of it
as applying an operator between any two elements in the list,
e.g. going from [1,2,3,4] to the result of
1 + 2 + 3 + 4. If the operator is not commutative,
that is x <op> y is not the same as
y <op> x, folding from the left will not be
the same as folding from the right, hence the need for both
foldl and foldr.
The foldr(init, oper) strategy takes a list of
elements and starts folding them from the right. It starts
after the rightmost element of the list. This means that
if we use the + operator with
foldr on the list [1,2,3,4],
we get the expression 1 + 2 + 3 + 4 + , which
obviously has a dangling +. The strategy
argument init is used to supply the missing
argument on the right hand side of the last plus. If the
init supplied is id,
[] will be supplied by default. We can see
this from the this trial run:
stratego> <foldr>(id, debug)
(4,[])
(3,(4,[]))
(2,(3,(4,[])))
(1,(2,(3,(4,[]))))
(1,(2,(3,(4,[]))))
With this in mind, it should be obvious how we can sum a list
of numbers using foldr:
stratego> <foldr(!0, add)> [1,2,3,4]
10
The related strategy foldl(s) works similarly to
foldr. It takes a two-element tuple with a list
and a single element, i.e. ([x | xs], elem). The
folding will start in the left end of the list. The first
application is s on (elem, x), as
we can see from the following trial run:
stratego> <foldl(debug)> ([1,2,3,4], 0)
(1,0)
(2,(1,0))
(3,(2,(1,0)))
(4,(3,(2,(1,0))))
(4,(3,(2,(1,0))))
Again, summing the elements of the list is be pretty easy:
stratego> <foldl(add)> ([1,2,3,4], 0)
10
In this chapter we got a glimpse of the most important strategies for manipulating lists. We saw how to construct and deconstruct lists, using build and match. We also saw how we can sort, merge, split and otherwise transform lists. The strategies for associative lists and sets gave an impression of how we can construct new abstractions from basic lists.
More information about list strategies available can be found in
the collections/list module, in the
library reference documentation.
Table of Contents
Strings, like all other primitive data types in Stratego, are
terms. They are built with the build (!) operator
and matched with the match (?) operator. Additional
operations on and with strings are realized through strategies
provided by the Stratego library. The most basic operations
on strings provided by the library are concatenation, length
computation and splitting. We will discuss operation each in
turn.
The library provides two variants of the string concatenation
operation. The first, concat-strings,
takes a list of strings and returns the concatenated result. The
second, conc-strings takes a two-element tuple of
strings and returns the concatenated result:
stratego><concat-strings> ["foo", "bar", "baz"] "foobarbaz"stratego><conc-strings ("foo", "bar") "foobar"
Once you have a string, you may want to know its length, i.e. the
number of characters it contains. There are two equivalent strategies
for determining the length of a string. If you come from a C background,
you may favor the strlen strategy. If not, the
string-length strategy may offer a clearer name.
The final basic operation on strings is splitting. There is a small family of
closely related strategies for this, which all do simple string tokenization.
The simplest of them is string-tokenize(|sepchars). It takes
a list of characters as its term argument, and must of course be applied
to a string.
stratego> <string-tokenize(|[' '])> "foo bar baz"
["foo","bar","baz"]
Another strategy in the tokenizer family is
string-tokenize-keep-all(|sepchars). It works exactly like
string-tokenize(|sepchars), except that it also keeps the
separators that were matched:
stratego> <string-tokenize-keep-all(|[' '])> "foo bar baz"
["foo"," ","bar"," ","baz"]
Even if you don't maintain a phone directory, sorting lists of
strings may come in handy in many other enterprises. The strategies
string-sort and string-sort-desc sort a
list of strings in ascending and descending order, respectively.
stratego>!["worf", "picard", "data", "riker"] ["worf", "picard", "data", "riker"]stratego>string-sort ["data","picard","riker","worf"]stratego>string-sort-desc ["worf","riker","picard","data"]
If you only have two strings to sort, it may be more intuitive to
use the string comparison strategies instead. Both
string-gt and string-lt take a two-element
tuple of strings, and return 1 if the first string
is lexicographically bigger (resp. smaller) than the second, otherwise
they fail.
stratego><string-gt> ("picard","data") 1stratego><string-lt> ("worf","data") command failed
Not directly a sorting operation, string-starts-with(|pre)
is a strategy used to compare prefixes of strings. It takes a string
as the term argument pre and must be applied to a string.
It will succeed if pre is a prefix of the string it was
applied to:
stratego> <strings-starts-with(|"wes")> "wesley"
"wesley"
We already said that strings are terms. As with terms, we can also
deconstruct strings, but we cannot use normal term deconstruction
for this. Taking apart a string with explode-string
will decompose a string into a list of characters. We can then
manipulate this character list using normal list operations and
term matching on the elements. Once finished, we can construct
a new string by calling implode-string. Consider
the following code, which reverses a string:
stratego>!"evil olive" "evil olive"stratego>explode-string [101,118,105,108,32,111,108,105,118,101]stratego>reverse [101,118,105,108,111,32,108,105,118,101]stratego>implode-string "evilo live"
This explode-string, strategy, implode-string
idiom is useful enough to warrant its own library strategy, namely
string-as-chars(s). The code above may be written
more succinctly:
stratego> <string-as-chars(reverse)> "evil olive"
"evilo live"
Sometimes, in the heat of battle, it is difficult to keep track of your
primitive types. This is where is-string and
is-char come in handy. As you might imagine, they will
succeed when applied to a string and a character, respectively. A minor
note about characters is in order. The Stratego runtime does not separate
between characters and integers. The is-char must therefore
be applied to an integer, and will verify that the value is within the
printable range for ASCII characters, that is between 32 and 126,
inclusive.
Finally, it may be useful to turn arbitrary terms into strings, and
vice versa. This is done by write-to-string and
read-from-string, which may be considered string I/O
strategies.
stratego><write-to-string> Foo(Bar()) "Foo(Bar)"stratego>read-from-string Foo(Bar)
Another interplay between primitive types in Stratego is between
numbers and strings. Converting numbers to strings and strings
to numbers is frequently useful when dealing with program
transformation, perhaps particularly partial evaluation and
interpretation. Going from numbers to strings is done by
int-to-string and real-to-string.
Both will accept reals and integers, but will treat is input
as indicated by the name.
stratego><int-to-string> 42.9 "42"stratego><real-to-string> 42.9 "42.899999999999999"
The resulting number will be pretty-printed as best as possible. In the second example above, the imprecision of floating point numbers results in a somewhat non-intuitive result.
Going the other way, from strings to numbers, is a bit
more convoluted, due to the multiple bases available in
the string notation. The simplest strategies,
string-to-real and string-to-int,
assume the input string is in decimal.
stratego><string-to-real> "123.123" 1.231230000000000e+02stratego><string-to-int> "123" 123
For integers, the strategies hex-string-to-int,
dec-string-to-int, oct-string-to-int
and bin-string-to-int can be used to parse
strings with numbers in the most popular bases.
Table of Contents
The rewriting paradigm of Stratego is functional in nature, which is somewhat contradictory to the imperative nature of hashtables. Normally, this doesn't present any practical problems, but remember that changes to hashtables "stick", i.e. they are changed by side-effect.
The Stratego hashtable API is pretty straightforward. Hashtables
are created by new-hastable and destroyed by
hashtable-destroy.
stratego>import libstratego>new-hashtable => h Hashtable(136604296)
The result Hashtable(136604296) here is a handle
to the actual hashtable. Consider it a pointer, if you will. The
content of the hashtable must be retrieved with the
hashtable-* strategies, which we introduce here. The
strategy hashtable-copy can be used to copy a hashtable.
Adding a key with value to the table is done with
hashtable-put(|k,v), where k is the key,
v is the value. Retrieving the value again can be
done by hashtable-get(|k).
stratego><hashtable-put(|"one", 1)> h Hashtable(136604296)stratego><hashtable-get(|"one") 1
The contents of the hashtable can be inspected with
hashtable-values and hashtable-keys.
Nesting is also supported by the Stratego hashtables. Using
hashtable-push(|k,v), a new "layer" can be added
to an existing key (or an initial layer can be added to
a non-existing key). Removing a layer for a key can be done
with hashtable-pop(|k).
stratego><hashtable-push("one",2)> h Hashtable(136604296)stratego><hashtable-get("one")> h [2,1]stratego><hashtable-pop(|"one")> h Hashtable(136604296)stratego><hashtable-get(|"one")> h [1]stratego><hashtable-remove(|"one")> h Hashtable(136604296)stratego><hashtable-values> h []
The library provides a rather feature complete implementation of indexed sets, based on hashtables. A lightweight implementation of sets, based on lists, is explained in Chapter 22.
Similar to hashtables, indexed sets are created with the
new-iset strategy, copied with
iset-copy and destroyed with iset-destroy.
stratego> new-iset => i
IndexedSet(136662256)
The resulting term, IndexedSet(136662256), is a handle
to the actual indexed set, which can only be manipulated through
the iset-* strategies.
Adding a single element to a set is done with
iset-add(|e), whereas an entire list can be added
with the iset-addlist(|es). Its elements can be
returned as a list using iset-elements.
stratego><iset-addlist(|[1,2,3,4,4])> i IndexedSet(136662256)stratego>iset-elements [1,2,3,4]
Notice that the result is indeed a set: every value is only represented once.
Using iset-get-index(|e), the index of a given
element e can be found. Similarly,
iset-get-elem(|i) is used to get the value for
a particular index.
stratego><iset-get-index(|3)> i 2stratego><iset-get-elem(|3)> i 4
Note that the indexes start at 0.
The set intersection between two sets can be computed with
the iset-isect(|set2) strategy. The
strategy iset-union(|set2) calculates the union
of two sets, whereas iset-subset(|set2)
checks if one set is a subset of another. Equality between
two sets is checked by iset-eq(|set2). These
strategies are all used in a similar way:
stratego> <iset-eq(|set2)> set1
A single element can be removed from the set with
iset-remove(|e). iset-clear will
remove all elements in a set, thus emptying it.
Table of Contents
This chapter explains the strategies available in the library for controlling file and console I/O.
The need for traditionally file I/O is somewhat diminished
for typical applications of Stratego. Normally, Stratego
programs are designed to worktogether connected by Unix
pipes. The programs employ io-wrap (or similar
strategies) that automatically take care of the input and
output. See Chapter 26 for details.
The primitive layer of Stratego I/O inherits its
characteristics from Unix. The basic I/O strategies
recognize the special files stdout,
stdin and stderr. Streams are
opened by fopen and closed with
fclose On top of this, a collection of
more convient strategies have been built.
The basic strategies for console I/O print
and printnl are used to write terms to
stdout or stderr (or any
other opened file). They both take a tuple. The first
element of the tuple is the file to write to, the
second is a list of terms. Each term in the list be
converted to a string, and and these strings will
be concatenated together to form the resulting output.
The printnl will also append a newline to
the end of the resulting string.
The following module should be compiled with strc, as usual.
module example
imports liblib
strategies
main =
<print> (stdout, ["baz"])
; <printnl> (stdout, [ "foo", 0, "bar" ])
After compiling this file, running it will give the following result:
$./example bazfoo0bar$
Notice how the string baz will be written
without a newline (or other space). Also, notice how the
terms in the list argument were concatenated.
When using these strategies in the Stratego Shell, some care must
be taken when using the std* files, as the following
example shows.
stratego> <printnl> (stdout(), [ "foo", 0, "bar" ])
foo0bar
The shell requires that you put an extra parenthesis after the
stdout.
The debug and error are convenience
wrappers around printnl. They will always write
their result to stderr. The error
strategy is defined as:
error = where(<printnl> (stderr, <id>))
It is used similarly to the printnl strategy:
stratego> <error> ["foo", 0, "bar"]
foo0bar
The debug strategy accepts any term, i.e.
not only lists of terms. The term will be written
verbatim:
stratego> <debug> [ "foo", 0, "bar" ]
["foo",0,"bar"]
The library provides a small set of simple file and directory
manipulation operations. Assume the directory
/tmp only contains the files
foo, bar,
baz. Elementary directory operations
can be done as illustrated below:
stratego><readdir> "/tmp" ["foo","bar","baz"]stratego><rename-file> ("/tmp/foo", "/tmp/bax") "/tmp/bax"stratego><remove-file> "/tmp/baz" []stratego><link-file> ("/tmp/bar", "/tmp/foo") "/tmp/foo"stratego><link-file> ("/tmp/bar", "/tmp/foo") "/tmp/foo"stratego><new-temp-dir> "/tmp" "/tmp/StrategoXTnsGplS"
The library contains a family of strategies which must be applied
to a File, and will return information about it.
these include isdir, isatty,
isfifo and islnk which are predicates
checking if a file is a directory, TTY, FIFO or a symbolic
link, respectively. To obtain a File object in the
first place, we should call file-exists followed
by filemode. Thus, checking if /etc
is a directory is done as follows:
stratego> <file-exists ; filemode ; isdir> "/etc"
The library also has another family of strategies for getting
information about files. These must be applied to a string
containing the filename. The family includes
is-executable, is-readable and
is-writeable.
stratego> <is-executable> "/bin/bash"
"/bin/bash"
Finally, the directory strategies also include the usual suspects for dealing with paths.
stratego><is-abspath> "../foo" command failedstratego><dirname> "/foo/bar/baz" "/foo/bar"stratego><base-filename> "/foo/bar/baz" "baz"stratego><get-extension "/tmp/foo.trm" "trm"stratego><abspath> "../foo" /home/karltk/source/oss/stratego/strategoxt-manual/trunk/../foo
There are also a few strategies for finding files. We shall
describe find-file(s). The other variants of
find-file are described in the library
documentation. The strategy find-file(s) finds one
file with a specific file extension in a list of directories. It
takes a two-element tuple. The first element is a file name as a
string, then second element is a list of paths, i.e. (f,
[d*]). The extension of f will be
replaced by what is produced by s, and the
directories given in [d*]. Consider the code below.
stratego> <find-file(!"rtree")> ("file.str", ["."])
This snippet will consider the filename file.str,
replace its extension with rtree and look through
the directories in the list ["."]. Effectively, it will
search for file.rtree in the current directory.
Opening a file is done with the fopen strategy. It takes
a two-element tuple, the first element is the filename as a string,
the second is the open mode, which is also a string. The most important
modes are read (r); write ("w") which opens and empty file
for writing, truncating any existing file with the same name; and
append (a) which appends to the file if it already exists.
After all file operations stream have been finished, it should be closed
with fclose, which will flush and close the file. Explicit
flushing can also be done with fflush.
It should be pointed out that reading and writing text files with Stratego
is rather rare. Normally, text files are read with a parser generated from
an SDF description and written using a pretty-printer defined in the
Box formalism. In rare cases, this may turn out be too heavy handed,
especially if the file format is simplistic and line-based. In this
instance, we can come up with an easier solution using
read-text-file and read-text-line.
Assume the file /tmp/foo contains the following
lines:
one two three
We can read this file in one big chunk into a string with the
read-text-file strategy, which must be applied to
a filename:
stratego> <read-text-file> "/tmp/foo" "one\ntwo\nthree\n"
Alternatively, for example if the file is large, we can read it line by line. In this scenario, we must open the file and get a handle to a stream.
stratego><fopen> ("foo.txt", "r") => inp Stream(136788400)stratego><read-text-line> inp "one"
The primary form of file I/O you will be using in Stratego is
reading and writing terms. As explained earlier, the terms
are stored on disk as either binary, compressed text or
plain text ATerms. Reading a term, no matter which storage
format, is done with the ReadFromFile strategy.
It is applied to a filename.
stratego> <ReadFromFile> "/tmp/foo.trm"
Foo(Bar)
To write a term to file, you can use WriteToTextFile
or WriteToBinaryFile. The binary format is
approximately eight times more space-efficient on average. Both
strategies take a two-element tuple where the first element is
the filename and second is the term to write. Writing the current
term requires a minor twist, which is shown here:
stratego> <WriteToBinaryFile> ("/tmp/bar.trm", <id>)
Foo(Bar)
It is also possible to read and write terms from and to strings,
using read-from-string and write-to-string.
Chapter 23 contains explanation of how these
strategies work.
The strategies for logging are used pervasively throughout the Stratego
toolchain. They are easy to use in your own applications, too. The
logging system is built on top of the
log(|severity, msg) and log(|severity, msg, term)
strategies. It is possible to use these directory, as the following
example demonstrates.
stratego>import util/logstratego>log(|Error(), "my error")
However, it is preferrable to use the high-level wrapper strategies
fatal-err-msg(|msg), err-msg(|msg),
warn-msg(|msg) and notice-msg(|msg).
Except for fatal-err-msg, these strategies will
return with the current term untouched, and write the message
as a side effect. The fatal-err-msg strategy will
also terminate the program with error code 1, after
writing the message.
Table of Contents
As Part II explained, the world of Stratego is one of small programs tied together using Unix pipes. The pipes carry the data, while configuration and control is passed between programs in the form of command line arguments. Incidentally, this is the same mechanism used by humans to invoke programs, and this eases understanding and debugging of XT compositions tremendously. Details about debugging is covered in Chapter 30. In this chapter, we will cover the mechanism available in Stratego for working with command line arguments.
When a compiled Stratego program is first started, the initial value of the current term is a list containing the command line arguments to the program. Fhe following program, foo, is a genuine "do nothing" program.
module foo imports liblib strategies main = id
In the course of this chapter, we will extend this program with new options and even a help screen for the user to enjoy. But first, let us compile and run foo with some arguments, to get an idea of where we stand.
$strc -i foo.str ...$./foo --help ["./foo","--help"]$./foo -i foo.str --extra --option -s ["./foo","-i","foo.str","--extra","--option","-s"]
From this interaction, we see that a list of the
arguments provided on the command line becomes the
initial term of the program. Each command line argument
becomes its own string element in the list, and the first
element of the list is the command used to invoke the
foo itself. Clearly, this list must be
interpreted somehow, for the arguments to have any meaning.
The library contains a collection of robust strategies
that deal with just this. The option handling strategies
will parse the argument list, let you set default values
for options and transparently deal with long and short
forms of the same option. Even more interesting, the
library provides so-called wrap strategies
that abstract away all of the dreary details of this
option handling, and also provide a default set of
options with some basic functionality.
Perhaps the most frequently used wrap strategy is
io-wrap (or its XTC equivalent,
xtc-io-wrap, which is not covered here).
In fact, io-wrap is a family of strategy,
which includes io-wrap(s),
io-wrap(opts, s) and
io-wrap(opts, usage, about, s). All of
these variants provide the same basic functionality. The
increasing number parameters allows you to override
default bevhavior, when you need to. When using
one of these strategies, a standard package of
command line handling will be provided to your users
through your program. Let us start with the simplest
case, io-wrap(s) and work our way from
there. Consider a revised edition of foo,
from above:
module foo imports liblib strategies main = io-wrap(id)
Here, we wrap the core logic of our program (just id
in our case) inside the io-wraper. If we run
foo with the --help
this time around, we will get a more instructive reply than
previously:
$ ./foo --help
Options:
-i f|--input f Read input from f
-o f|--output f Write output to f
-b Write binary output
-S|--silent Silent execution (same as --verbose 0)
--verbose i Verbosity level i (default 1)
( i as a number or as a verbosity descriptor:
emergency, alert, critical, error,
warning, notice, info, debug, vomit )
-k i | --keep i Keep intermediates (default 0)
--statistics i Print statistics (default 0 = none)
-h|-?|--help Display usage information
--about Display information about this program
--version Same as --about
Description:
All of a sudden, our program is a well-behaved citizen
in the command line world. It answers to
--help, and appears to have a few other
tricks up its sleeve to. For example, the input term
to foo can now be specified using the
-i option, and output can be stored to
a file using the -o option.
So does this actually work? All for free? Let's test with
putting the following term into the file
term.trm:
Yes(It(Works))
Bursting with excitement, we try:
$ ./foo -i term.trm
Yes(It(Works))
And if that's not enough, there is even a bit of extra
convenience provided by io-wrap: If
-i is not provided,
stdin is read. Similarly,
stdout is written to if
-o is not specified.
So, using io-wrap is all you have to do for your program
to gain a minimal, but functional set of command line options. As a
bonus, these options also make your program compatible with XTC; it
can be composed with other XTC components.
It is often necessary for programs to expose switches to turn
functionality on and off, or to read extra configuration knowledge
from external files. All these cases require additional command
line options, so we need a mechanism for extending
the basic io-wrap(s) strategy. The preferred way of
adding new options is to use the io-wrap(opts,s)
strategy, providing it with a strategy encoding the options.
When adding a new option, we must decide whether this option
will require a argument of its own, or not. The term
ArgOption is used to construct options that take
arguments and Option is the term used for on/off
switches. Suppose we want to expose an option
--verify that enables the user to run our
transformation in a self-verifying mode. This is clearly an
on/off switch, and therefore a job for Option.
Adding this option to our program foo gives us the following code:
module foo
imports liblib
signature
constructors
Verify : Option
strategies
main = io-wrap(
Option(
"--verify"
, <set-config> (Verify(), "on")
, !"--verify Turn on verification")
, do-foo)
do-foo = ...
Note that we made a new term type, Verify, to serve as
our switch symbol. Inside the real logic of program,
given by do-foo, we would write
<get-config> Verify to get the state of the
Verify switch. In the case where the user had specified
--verify on the command line,
get-config would result in the term "on",
taken from the declaration of our verify Option. If
the did not add --verify to his command line
arguments, <get-config> Verify will fail.
Options with arguments is provided through ArgOption.
The use is pretty much identical to that of Option.
Assume our transformation needs a bit of help from configurable
processing tables (whatever that might be), and that we want these
tables configured at runtime, using the -p option.
We want to add another alternative to the opts argument
of io-wrap:
main = io-wrap(
Option(....)
+
ArgOption(
"-p"
, where(<extend-config> ("-p", [<id>]))
, !"-p file Use processing table in file")
, id)
Note how we compose options with the choice operator (+).
With this addition, our users can now specify their elusive processing
tables with the -p. The arity of this option is checked
automatically. That is, if the user adds -p to his
argument list without specifying a file afterwards, this will be signaled
as an error, and the usage screen will be printed. Once the user has
read this and corrected the error of his ways, the value (the filename)
provided via -p can be obtained using the
get-option strategy. If no -p was
specified, get-option will fail. Sometimes, this failure
may be inappropriate, and a default value is desired instead. If you
browse through Stratego code, you may come across the following idiom
for dealing with this situation:
get-config-p =
<get-config> "-p" <+ ![]
This is all you need to know about basic command-line option processing. When in doubt, you are advised to refer to the detailed API documentation is available in the API reference.
If your program is primarily intended for human use, you are encouraged to complete your program's option configuration with a short description of what your tool does.
We can easily add a short description and also an about section.
The description is shown as part of the help screen
(displayed with --help), whereas the about
section is displayed when the arguments to foo
contain --about. It is customary for the about
screen to contain copyright notices and credits.
main = io-wrap(
...
, foo-tool-usage
, foo-tool-about
, id)
foo-tool-usage =
default-system-usage(
!["Usage: foo -p proctbl [options]"]
, ![ "This program verifies the input against a processing table.\n"]
)
foo-tool-about =
<echo> "Written by Alan Turing <alan@turing.org>"
After compiling this version of foo, invoking
it with --help give the following help screen:
$ ./foo --help
Usage: foo -p proctbl [options]
Options:
--verify Turn on verification
-p file Use processing table in file
-i f|--input f Read input from f
-o f|--output f Write output to f
-b Write binary output
-S|--silent Silent execution (same as --verbose 0)
--verbose i Verbosity level i (default 1)
( i as a number or as a verbosity descriptor:
emergency, alert, critical, error,
warning, notice, info, debug, vomit )
-k i | --keep i Keep intermediates (default 0)
--statistics i Print statistics (default 0 = none)
-h|-?|--help Display usage information
--about Display information about this program
--version Same as --about
Description:
This program verifies the input against a processing table.
If we invoke our splendid program foo with
the --about option, we can now observe:
$ ./foo --about
Written by Alan Turing <alan@turing.org>
Not all programs written in Stratego intended for processing ATerms.
For these programs, the full I/O functionality provided by
io-wrap may often turn out to be inappropriate. An
alternative way of dealing with parameters is also provided by
the library, centered around the option-wrap family of
strategies. option-wrap works analogously to
io-wrap, but does not provide the -i
and -o options, nor does it read anything from
stdin automatically.
The default set of options provided by option-wrap
is shown below:
--verify Turn on verification -h|-?|--help Display usage information --about Display information about this program --version Same as --about
Adding new options is identical to what we already explained
for io-wrap.
Table of Contents
StrategoUnit or SUnit is a Unit Testing framework for Stratego inspired by JUnit. The idea is to specify tests that apply a strategy to a specific term and compare the result to the expected output. The tests are combined into a test suite, which runs all tests and reports the number of successes and failures. When all tests pass, the program exits with status 0, otherwise it exists with status 1 to flag the error to the calling program, which is typically a makefile.
Module list-zip-test.str in the Stratego
Standard Library is an example test suite. SUnit test suites can
be compiled to an executable program. When run the program gives
the following output:
test suite: list-zip-test nzip0-test zip-test1 zip-test2 successes: 3 failures: 0 (3,0)
An extract from the module shows how a test suite can be set up:
module list-zip-test
imports list-zip sunit
strategies
main =
test-suite(!"list-zip-test",
nzip0-test;
zip-test
)
nzip0-test =
apply-test(!"nzip0-test"
,nzip0(id)
,!["a","b","c"]
,![(0, "a"), (1, "b"), (2, "c")]
)
The test-suite strategy takes a string and a strategy. The
strategy is typically a sequential composition of calls to unit
tests. Unit tests such as nzip0-test
are defined using one of the unit-test strategies from module
sunit, which is in the standard library.
The prototypical unit test is composed with the
apply-test strategy, which takes a
name, the strategy that is being tested, the input term, and the
exptected output term. Note that the name, input, and output
term must be specified in strategies, which means that if
literal terms are used then you must build them using the !
operator.
apply-test(!"test3"
, ltS
, !("3","5")
, !("3","5")
)
It is also useful to test that a strategy fails if applied to a
certain input. The ordinary apply-test
cannot be used for this because it requires an output term to
which the result will be compared. For testing failure the
apply-and-fail strategy is available in
sunit. It ensures that the strategy fails if applied to a
certain input.
apply-and-fail(!"is-double-quote 3" , is-double-quoted , !"\"fnord" )
Sometimes a test just want to check some condition on the output
of a strategy application, without actually specifying the
output itself. The apply-test strategy
cannot be used for this because it performs an equivalence test
of the required output and the actual output. In this case
apply-and-check can be used. This
strategy takes 4 arguments: a name, a strategy (s) to test, an
input and a strategy that will be applied to the result of
applying s to the input. This strategy must succeed if the
output is correct, or fail if the output is incorrect.
new-test =
apply-and-check(!"new test",
(new, new)
, !(1, 1)
, not(eq); (is-string, is-string)
)
XTC is the preferred system for writing components in Stratego/XT. Testing that an XTC component acts as intended is not much more difficult than for individual strategies. As the semantics of the interfaces to XTC programs is open-ended, there is currently no generic testing framework for handling all the details.
Nevertheless, adapting the unit testing framework explained above for
testing your components is easy. Consider the strategy
xtc-apply-test, given below.
xtc-apply-test(|nm, prog, args, inp, outp) =
xtc-temp-files(
apply-test(!nm,
write-to
; xtc-transform(!prog, !args)
; read-from
, !inp
, !outp
)
)
This is a straightforward extension of apply-test. It
will invoke the XTC program given in the prog term argument
with the list of command line arguments in args. The input to the
program is the term given by inp. The resulting term after
prog has been run is checked against outp.
If they match, the test succeeds.
The simple code above does not account for additional file arguments to
prog. This may be useful if prog if
prog is, say, a pretty-printer which takes both a document
and a style sheet as arguments. The code below provides an example of how
this may be handled.
xtc-apply-pp-test(|nm, prog, ssheet, args, inp, outp) =
xtc-temp-files(
apply-test(!nm,
where(<print-to> [ssheet] => FILE(f))
; write-to
; xtc-transform(!prog, <concat> [ args, "--stylesheet", f])
; read-from
, !inp
, !outp
)
)
Table of Contents
In Chapter 3, we explained how the Stratego/XT universe is built from small components, each a separately executable program. Many such components are provided for your reuse by the Stratego/XT distribution. We have already seen some of these in action throughout Part II. In this chapter, we will first explain how to compose existing components together, and then proceed to explain how you can make your own Stratego programs into reusable XT components.
Before we can compose XT components, we must place them in a component repository. This is referred to as registration. The registration associates each component with a name, a path and a version. The name is used later to look up components, and map their names to their actual location in the file system. This is very handy when you program with XT components. Inside our Stratego programs, we only have to specify the name of the program we want executed, and the XTC machinery will automatically figure out which program to execute, set up the piping, deal with temporary files, and even perform the execution and parameter passing for us.
In this section, we will cover the registration and lookup mechanisms in some detail.
An XTC repository is a collection of programs and data files. The programs, which we usually refer to as XT components, must be registered explicitly using the xtc tool before they can be used. This is also the case for the data files. A normal program transformation system built with Stratego/XT will contain an XTC repository, where all its components have been registered. Though this registration is done automatically for you by the Stratego build system, it will prove instructive to know what takes place behind the scenes, by the understanding the xtc command (refer to Chapter 29 for an explaination of how to configure the Stratego/XT build system to automatically register your XT components).
Suppose our project, called Ogetarts, has been installed
into .../ogetarts
(where ... is a path of your choice).
A typical directory layout for this project would include
the following directories:
.../ogetarts/
share/
ogetarts/
bin/
libexec/
lib/
The part we are interested in now is the directory
.../ogetarts/share/ogetarts/. This
is where the registry for the XTC repository is normally
placed, in the file XTC. Assuming we
already have the XT component foo2bar
placed in .../ogetarts/libexec/. The
following xtc invocation will register
it with the Ogetarts registry:
$ xtc -r .../ogetarts/share/ogetarts/XTC register -t foo2bar -l .../ogetarts/libexec -V 1.0
This command will also take care of creating a fresh
XTC registry file if it does not already
exist. The -l specifies the path to the component
being registered, and -t specifies its name. This
name is used for lookup purposes later. The -V is
used to associate a version number with a given program. It is possible
to include the version number in the lookup of a component, to find
a particular version of a particular component, but this is not
common practice, and should be avoided. However, every registration
must have include a version number.
The XTC system provides a form of inheritance, whereby one repository can refer to another. You may also think of it as a scoping mechanism on the namespaces of repositories. When searches for components fail at the local repository, the imported repositories will be searched in turn.
It is practically always necessary for your project to import the Stratego/XT repository, as most transformation systems built with Stratego/XT reuse many of the XT components. The following command adds the Stratego/XT repository to our project:
$ xtc -r .../ogetarts/share/ogetarts/XTC import /usr/share/StrategoXT/XTC
In case you wondered, the current version of XTC has no mechanism
for declaring some components as private, and others public. Once
a component c is registered in an XTC repository
r, all other repositories importing r
can ask for c.
When you have registered your components or imported other
repositories, you may inspect your repository to see that everything
looks good. This is done using the query
option to xtc. Using query,
you can either look for a particular component, or list all
registrations in a given repository.
The following command will search the Ogetarts repository for the sglr component. This component was not registered by us, but is inherited from the Stratego/XT repository.
$ xtc -r .../ogetarts/share/ogetarts/XTC query -t sglr
sglr (3.8) : /usr/bin/sglr
Alternatively, we can list all registrations, in one go:
$ xtc -r .../ogetarts/share/ogetarts/XTC query -a
foo2bar (1.0) : .../ogetarts/libexec/foo2bar
stratego-lib (0.16M1) : .../stratego-lib
...
The format of this list is name (version) : path,
where name, we remember, is the handle used to
look up the given component. The list follows a pre-determined
order. First, all registrations in the Ogetarts will be displayed.
Here, foo2bar is our only component. After the
local components, the contents of each imported repository will
be displayed. In our case, we only imported Stratego/XT, and the
first component in Stratego/XT is stratego-lib. The
other 490 registrations have been omitted, for the sake of clarity.
Much of the scalability of Stratego/XT comes from its component
model, thus it is important to know how to design your own programs
to take advantage of this infrastructure. Fortunately, the
programming interface of XTC consists of a small set of clearly
defined strategies. If you are already familiar with
io-wrap, as introduced in
Chapter 26, this will be even easier to
comprehend.
There are three main usage scenarios for the XTC API. Either you use the API to create a new XT component of your own, or you use it to invoke an XT component from your Stratego program (which need not be an XT component), or both; you are writing an XT component which calls other XT components.
The simplest way to make an XT component is to wrap your
top level strategy with the xtc-io-wrap
wrapper. This automatically bestows your program with
basic command line option parsing capabilities, and also
basic I/O.
The following is an example of a trivial XT component which just passes through the term passed to it.
module xtcid imports liblib strategies main = xtc-io-wrap(xtcfoo) xtcfoo = id
As with the io-wrap strategy explained in
Chapter 26, a default set of
command line options is provided by xtc-io-wrap.
After compiling the xtcid.str,
we can run it to inspect the default set of options.
$ ./xtcid --help
Options:
-i f|--input f Read input from f
-o f|--output f Write output to f
-b Write binary output
-S|--silent Silent execution (same as --verbose 0)
--verbose i Verbosity level i (default 1)
( i as a number or as a verbosity descriptor:
emergency, alert, critical, error,
warning, notice, info, debug, vomit )
-k i | --keep i Keep intermediates (default 0)
--statistics i Print statistics (default 0 = none)
-h|-?|--help Display usage information
--about Display information about this program
--version Same as --about
Description:
This is normally all you have to do in order to have a
working XT component. You can add additional options using
the Option and ArgOption, as
explained in Chapter 26, by
wrapping your toplevel strategy with
xtc-io-wrap(extra-opts, s) instead of
xtc-io-wrap(s). In either case, your
program will now automatically read the input term
from the file specified with -i, pass
this to s, then write the result of
s to the file specified by
-o. When -i or
-o are not specified,
stdin and stdout
will be used instead, respectively.
$echo "My(Term)" | ./xtcfoo -o myterm.trm$cat myterm.trm My(Term)$
In some situations, it does not make sense for your component to accept an
input term, or to generate and output term. That is, your component may be
a data generator, or a data sink.
In these cases,your component should rather use
xtc-input-wrap, in the case of a sink, or
xtc-output-wrap, in the case of a generator.
The following programs shows a trivial generator, which
produces the term "foo" when invoked.
module xtcfoo imports liblib strategies main = xtc-output-wrap(xtcfoo) xtcfoo = !"foo" ; write-to
xtcfoo strategy is our top level strategy. Note how it ends in
a call to write-to. The argument s to
xtc-output-wrap(s) must result in a file, not a term. Copying
the current term to a file, is taken care of by the write-to
strategy. write-to will create a fresh temporary file and
write the current term to it. The inverse of write-to is
read-from which reads a term from a file. This latter strategy
is used together with xtc-input-wrap, analogously to the
example above.
In both cases (xtc-input-wrap and
xtc-output-wrap), you may add additional command
line options, by using variants of the wrappers which
accept extra options, xtc-input-wrap(extra-options, s)
and xtc-output-wrap(extra-options, s),
respectively.
Checking Component Dependencies.
If you write a component which depends on other components
as part of its operation, you are encouraged to add
dependency checking using the
xtc-check-dependencies. This is a two step
procedure: First, you add the --check
option to your components command-line options,
by adding check-options(deps) to the
extra-opts argument of
xtc-io-wrap. Afterwards, you should call
xtc-check-dependencies as part of your
option-processing.
Going back to our simple xtcid program, we
would add the --check with functionality, as
follows:
module xtcid imports liblib strategies main = xtc-io-wrap(check-options(!["sglr", "foo2bar"]), xtcid) xtcid = xtc-check-dependencies ; id
After recompiling xtcid, the user can now
ask your component to do a self-check of its dependencies,
by calling it with the --check. You may
want to piggy-back on this option, adding other kinds of
self-checks, such as data consistency checking.
Graceful Termination.
As you have witnessed, the implementation of the XTC model
makes heavy use of temporary files. It is important that
these files are cleaned up after exectuion of your program.
In all programs we have seen so far, this was taken care of
automatically by the wrappers. But what happens if you want
to terminate your program in the middle of execution, by
calling exit, for example? In that case, the
temporary files will not be removed properly. A safe way
of exiting XTC programs is provided by the
xtc-io-exit strategy. This strategy is a
plugin replacement for exit, but takes
care of cleaning any and all temporary files created by
your program before terminating.
Now that we know how to create XT components, and we also know that the Stratego/XT environment provides many reuseable XTC programs, we should take a bit of time to explain how we can invoke these inside our Stratego programs. It is important to realize that your Stratego program need not itself be an XT component before it can call out to other XT components. Both XTC programs and normal Stratego programs call XT components in the same way.
Before we proceed, we need to create a small XTC program
that we can call. The following is an XTC version of
the inc strategy. When invoked on an
integer n, it will return
n + 1.
module xtcinc imports liblib strategies main = xtc-io-wrap(read-from ; <add> (<id>, 1) ; write-to)
Let us quickly whip up a client for this component, that
invokes xtcinc on the integer
1:
module xtcclient imports liblib strategies main = !1 ; xtc-transform(!"xtcinc")
Let us a compile and run this program.
$ ./xtcclient
[ identity crisis | error ] No XTC registration for xtcinc found
./xtcclient: rewriting failed
Harking back a few sections, we should now realize that we forgot
to register xtcinc in a repository. We already
know how to do this. For the sake of this demonstration, let
us create the XTC registry in the same
directory as the source code:
$ xtc -r ./XTC r -t xtcinc -V 1.0 -l `pwd`
If we were to run our program xtcclient again
at this point, we would still get the same error. This is because
we have not told xtcclient which repository
it should use. This is done by the --xtc-repo
option to the Stratego compiler.
$ strc --xtc-repo ./XTC -i xtcclient.str
....
This should complete the necessary steps: We have created the XTC program
xtcinc, we have registered it in the XTC registry in
./XTC, and we have told strc to
compile our client program, xtcclient against this
repository. We should be all set to run our composition. Let's try.
$ ./xtcclient
2
At last, it works. We have connected two components. By changing the
internals of our components, we can change them to process any terms we
want, and we can of course also add additional components into the mix,
all using the same basic steps we have explained here. Having to remember
the --xtc-repo option to strc all the
time is a bit annoying, but as we shall in
Chapter 29, this will be taken care of
automatically by the Stratego/XT build system.
Finding XTC Data Files.
We have just seen how to use XTC programs from a repository,
but so far, we have said nothing about any data files we have
registered. This is where the xtc-find-file strategy
comes in handy. Let us go through the process of creating a term,
registering it, and then using it inside our program.
Suppose the file myterm.trm contains the
following term, written in plain text:
My(Term)
Calling xtc as follows, will register it in the local repository we have already created.
$ xtc -r ./XTC r -t myterm.trm -V 1.0 -l `pwd`
This will register the file myterm.trm
under the name myterm.trm, which we can use
to look it up from inside our programs later. Let us make a
new program that does just this.
module xtcload imports liblib strategies main = <xtc-find-file> "myterm.trm" ; read-from
xtc-find is applied to a string, which must be
the name of an already registered data file in the
repository. As before, we have to compile our program
using strc, and remember to include
the --xtc-repo option.
$ strc -i xtcload.str --xtc-repo ./XTC
We can now run our freshly compiled program.
$ ./xtcload
My(Term)
The result is as we anticipated. Congratulations! You have now mastered the basics of the XTC mechanics.
This chapter introduced you to the mechanics of the XTC model. We saw how to maintain a registry of XT components using the xtc tool, and also how to write XTC compositions in Stratego. Additional detail about the XTC API can be found in the API reference documentation. The complete documentation for the xtc tool is given on the manual page (xtc).
Table of Contents
There are two typical scenarios for building Stratego programs. The first, and simplest, is to execute the compiler by hand on the command line in order to build one artifact (a program or a library). The second is to set up a full build system is based on the GNU Autotools. Both scenarios will be covered in this chapter.
Here we describe how to use the Stratego compiler for small projects and for compiling one-off examples on the command-line. We recommend that you use Autotools for larger projects, i.e. when you need to build multiple artifacts (see the next sections).
Invoking the compiler on simple programs which only depend on the Stratego library is straightforward:
$ strc -i myprog.str
This produces the executable file myprog. When
your program depends on other Stratego packages (libraries),
you need to provide the compiler with proper include paths (for
finding the module definitions) and linking arguments (for linking
the libraries with the final executable). For convenience, you
should define an alias called strcflags as follows:
$ alias strcflags="pkg-config --variable=strcflags "
By calling strcflags with the the name of a
specific package, e.g. java-front, all necessary
include paths and library arguments will be provided for you. This
gives rise to the following idiom:
$ strc -i myprog.str $(strcflags dryad java-front)
Note that providing several arguments (packages) to strcflags is allowed.
By default, the Stratego compiler will dynamically link all libraries. To
enable static linking instead, you must add the command line options
-Xlinker -all-static:
$ strc -i myprog.str -Xlinker -all-static
This ensures that the myprog executable is statically
linked (and therefore has no external dependencies).
Setting up a build system for Stratego involves the Autotool programs automake, autoconf and libtool. In addition, Stratego provides a new tool called autoxt. If you are familiar with the Autotools, setting up a project for Stratego should be rather easy. If this is unfamiliar ground to you, don't fear. We will walk through it slowly in the next sections, but a full treatise is beyond the scope of this tutorial.
After creating your project directory, let's call it
ogetarts, the first thing you should do is
populate it with the basic build system files, namely
configure.ac,
bootstrap,
Makefile.am. Additionally, you may want to
add ChangeLog,
AUTHORS, NEWS and
README, but these are not essential. If you
want to support the creation of RPMs, then you need to create a
file ogetarts.spec.in.
For a normal Stratego project, with a syntax, some stand-alone
tools, and a library, we suggest the project layout given below
(directories end in /). We will discuss the
all the components of this hierarchy in turn.
ogetarts/
bootstrap
configure.ac
Makefile.am
syn/
Makefile.am
lib/
Makefile.am
tools/
Makefile.am
The build system is kickstarted by the
bootstrap script. This script is
responsible for generating a configure
script. When run by the user of your package, the
configure script will autodetect the
Stratego compiler and other tools required to build your
project. The concept of generation is very central to
autotool-based build systems. The configure
script is generated from a configure.ac
declaration by the autoreconf tool. The
Makefiles are generated from
Makefile.in files by the
configure script, and
Makefile.in files are generated from
Makefile.am files by
automake. Simple, huh? Generally, the idea is
that complicated scripts and makefiles can be generated from
high-level declarations using tools. Let's start with the
bootstrap script.
#! /bin/sh autoxt || exit 1 autoreconf -ifv || exit 1
The bootstrap script should be an
sh (or bash) shell script
that takes care of running autoxt and
autoreconf, as shown above. Note that we rely
on reasonably recent versions of autoconf and
automake.
Assume we are in a palindromic mood and want to name our project
Ogetarts. The following file will then provide a reasonable
starting point for the configure.ac file.
AC_PREREQ([2.58]) AC_INIT([ogetarts],[0.1],[ogetarts-bugs@ogetarts.org]) AM_INIT_AUTOMAKE([1.7.2 -Wall -Wno-portability foreign]) # set the prefix immediately to the default prefix test "x$prefix" = xNONE && prefix=$ac_default_prefix XT_SETUP XT_USE_XT_PACKAGES AC_PROG_CC AC_PROG_LIBTOOL ### OUTPUT ############################# AC_CONFIG_FILES([ Makefile syn/Makefile lib/Makefile tools/Makefile ]) AC_OUTPUT
Most of this is standard boilerplate. The foreign
option specified in the arguments of AM_INIT_AUTOMAKE
tells automake not the check that the package conforms to GNU
package standards, which requires files such as
ChangeLog, AUTHORS,
COPYING, NEWS and
README. For this small example, we do not
want create all these files. You can leave out the
foreign option if you want to make a complete GNU
package.
The important line is XT_USE_XT_PACKAGES which is a
macro invocation that will extend to shell script code that looks
for the ATerm library, the SDF tools and Stratego/XT,
respectively. These macros are provided by the
autoxt tool, via a macro file called
autoxt.m4. It provides the following macros.
XT_SETUP-
Sets up a Stratego package by setting standard flags of the C compiler and linker for Stratego programs.
XT_USE_XT_PACKAGES-
Adds configuration options to configure the package with the location of the ATerm library, SDF2 Bundle and Stratego/XT.
XT_PRE_RELEASE-
Adds the suffix
pre${SVN_REVISION}to thePACKAGE_VERSIONandVERSIONvariables. This is a naming convention for unstable packages that we are using in our release management system. If you are not building your package in our buildfarm, then you do not need to invoke this macro. XT_DISABLE_XTC_REGISTER-
Disables the creation of an XTC repository. By default all programs and files are registered in an XTC repository.
XT_USE_BOOTSTRAP_XT_PACKAGES-
Similar to
XT_USE_XT_PACKAGES, this macro adds configuration options to configure the package with the location of the ATerm library, SDF and Stratego/XT. However, the macro will only check the existence of these packages if the option--enable-bootstrapis given to theconfigurescript. In other case, it will only look for the Aterm Library and Stratego Libraries. Also, XTC registration is disabled. This macro is used for packages that need to be very portable, including native Microsoft Windows. XT_SVN_REVISION-
Determines the SVN revision and makes this number available to Stratego programs.
At the end of the configure.ac above, the invocation
of the AC_CONFIG_FILES macro lists other
important files of the build system, particularly the
Makefiles. We must provide these, but remember
that these are generated from .in files
which in turn come from .am files. Hence, we
need to provide some Makefile.am files. The
Makefile.am for the root of the project
should look like:
include $(top_srcdir)/Makefile.xt SUBDIRS = syn lib tools BOOTCLEAN_SUBDIRS = $(SUBDIRS) DIST_SUBDIRS = $(SUBDIRS) EXTRA_DIST = ACLOCAL_AMFLAGS = -I .
Again, most of this is boilerplate. The important point here is
that SUBDIRS = syn lib tools will eventually result
in rules that tell make to delve into these
directories. We will explain below how the
Makefile.ams for each of the source directories
should look like. For now, you can just create empty
Makefile.am files in the sub-directories
syn/,
lib/, and tools/. This
allows you to bootstrap and configure the package:
$mkdir syn lib tools$touch syn/Makefile.am lib/Makefile.am tools/Makefile.am$chmod u+x bootstrap$./bootstrap$./configure$make
The content of the empty Makefile.am files depends
on whether you are building a parser, stand-alone Stratego
programs, or a Stratego library. We will discuss each variant
separately, but you are of course free to mix several of these in
your project, like we do in this project: In
lib lives the library parts of Ogetarts, in
syn a parser is generated, and in
tools we place the command-line programs.
In Chapter 11, we showed how to
compile stand-alone Stratego programs using the strc
compiler. This process is automated by the build system, provided you
supply a suitable Makefile.am. Take the
one provided below as a starting point.
include $(top_srcdir)/Makefile.xt include $(wildcard *.dep) bin_PROGRAMS = ogetarts ogetarts_LDADD = $(STRATEGO_LIB_LIBS) $(STRATEGO_RUNTIME_LIBS) $(ATERM_LIBS) STRINCLUDES = -I $(top_srcdir)/lib -I $(top_srcdir)/syn STRCFLAGS = --main io-$* EXTRA_DIST = $(wildcard *.str) $(wildcard *.meta) CLEANFILES = $(wildcard *.c) $(wildcard *.dep)
This file should be placed in tools/. The
following list explains the various parts occurring in the file.
include $(top_srcdir)/Makefile.xt-
Includes the various Stratego/XT make rules in this Makefile, for example for the compilation of Stratego programs and parse tables.
include $(wildcard *.dep)-
The Stratego compiler generates
.depfiles which contain information about module dependencies. When these.depfiles are included, a rebuild is forced when a dependent file changes. bin_PROGRAMS-
A list of stand-alone Stratego programs that should be compiled and installed in the directory
$prefix/bin. For each program, a corresponding.strfile must exist. In this case, the most trivialogetarts.strmodule could look like:module ogetarts imports libstratego-lib strategies io-ogetarts = io-wrap(id)
program_LDADD-
Stratego programs reuse various libraries, such as the ATerm library, the Stratego runtime and the Stratego library. This declaration tells the build system to link the program ogetarts with these libraries. If you use more libraries, such as the library
libstratego-sglrfor parsing, then you can add$(STRATEGO_SGLR_LIBS). All libraries follow this naming convention, for example the variable$(STRATEGO_XTC_LIBS)is used for the librarylibstratego-xtc. If you also have your own library in this package, then you can add$(top_builddir)/lib/libogetarts.la. STRCFLAGS-
Contains compiler flags passed to the Stratego compiler. A typical flags is
--main. In this case, the declaration tells the Stratego compiler that the main stratego of a programfooisio-foo(instead of the defaultmain). It is recommended that include directories are passed via theSTRINCLUDESvariable. STRINCLUDES-
A list of additional includes necessary for a succesful compilation, of the form
-I <dir>. They will be passed unchanged to the strc compiler. The Stratego compiler will then look in these directories for Stratego modules. EXTRA_DIST-
Specifies which auxilary files have to be included in the distribution, when doing a
make dist. In this case, we want to distribute all the Stratego modules and their.meta(which do not always exist) CLEANFILES-
Files to be deletes these files when the
make cleancommand is issued. In this case we instruct automake to remove the.cand.depfiles that are generated by the Stratego compiler. BOOTCLEANFILES-
Files to be deleted when
make bootcleanis issued. In addtion, the files specified inCLEANFILESwill also be deleted.
As we can see from the list above, the bin_PROGRAMS
is a list of the stand-alone programs that should be compiled in
this directory. For each program, a corresponding
.str must exist, in this case, a
ogetarts.str file. For each program the
Stratego compiler will be passed the STRINCLUDES and
STRCFLAGS variables. The program_LDADD
variable is used to add additional native libraries that should be
linked as part of the C compilation process.
STRINCLUDES and STRCFLAGS were explained
above.
autoxt installs
Makefile.xt, a collection of Automake rules
for compiling Stratego programs and applying other XT tools, such
as signature generation. Using this makefile, a makefile reduces
to a declaration of programs to be compiled. The makefile
automatically takes care of distributing the generated C code. The
specification will only be compiled when it is newer than the C
code.
In Chapter 6 we introduced you to the
Syntax Definition Formalism SDF for specifying grammars, and
showed you how to use pack-sdf and
sdf2table to construct parse tables out of
these definitions. The grammar can also be used to derive
Stratego signatures and regular tree grammars. Not surprisingly,
the build system is equipped to do this for you. Consider the
Makefile.am provided below.
include $(top_srcdir)/Makefile.xt include $(wildcard *.dep) DEF_TBL = Ogetarts.def Ogetarts.tbl RTG_SIG = Ogetarts.rtg Ogetarts.str sdfdata_DATA = $(DEF_TBL) $(wildcard *.sdf) pkgdata_DATA = $(RTG_SIG) EXTRA_DIST = $(DEF_TBL) $(RTG_SIG) $(wildcard *.sdf) CLEANFILES = $(DEF_TBL) $(RTG_SIG) SDFINCLUDES = SDF2RTG_FLAGS = -m $* PGEN_FLAGS = -m $*
This file should be placed in syn/. The
following list explains the various parts occurring in the file.
sdfdata_DATA-
The important declaration in this file is
sdfdata_DATA. They files listed for this variable will be installed as part of amake installinto the directory$prefix/share/sdf/$packagename. For convenience, we have defines the.defand.tblfiles, in a separate variableDEF_TBL. The build system knows how to generate.deffiles from.sdfusing pack-sdf, and.tblfiles from.deffiles using sdf2table. Note that there must be an SDF moduleOgetarts.sdf, which is the main module of the syntax definition. For example:module Ogetarts hiddens context-free start-symbols Expr exports context-free syntax IntConst -> Expr {cons("Int")} context-free priorities Expr "*" Expr -> Expr {left, cons("Mul")} > Expr "+" Expr -> Expr {left, cons("Plus")} lexical syntax [0-9]+ -> IntConst [\t\n\r\ ] -> LAYOUT pkgdata_DATA-
This variable defines a list of files that will be placed in
prefix/share/package-namepkgdata_DATAto tell the build system to build a Stratego signature (Ogetarts.str) and a regular tree grammar (Ogetarts.rtg) from theOgetarts.def. Including signatures and source code with your program is useful when you want other projects to extend and compile against yours. EXTRA_DIST-
Similar to the makfile for building Stratego programs, we use
EXTRA_DISTto define the files to distribute. In this case, we also distribute the derived.def,.tbl,.rtg, and.str, which is used to avoid a dependency on the full Stratego/XT. If this is not required, then we can leave these files out of the distribution. CLEANFILES-
In
CLEANFILESwe specify that we want make to remove the generated files when running amake clean. PGEN_FLAGS-
This variable is used to pass flags to the parsetable generator, sdf2table. The definition in this makefile defines the main module to be
$*, which is the basename of the.deffile that is used as the input to the parser generator. This is typical for most makefiles, since the default main module isMain. SDF2RTG_FLAGS-
Similar to
PGEN_FLAGS, this variable is used to pass flags to the tool sdf2rtg, which generates a regular tree grammar for an SDF syntax definition. Again, we define the main module of the syntax definition to be the basename of the file. SDFINCLUDES-
Similar to
SDFINCLUDES, you can define directories to search for SDF modules using theSDFINCLUDESvariable. In addition to the option-Iyou can also include modules from an SDF definition:dir-Idef.file.def
Stratego allows you to freely organize the Stratego modules of
your project, but we recommend to have a separate library in
the directory lib/. Each
.str file placed inside this directory
becomes a module for your library. For sufficiently large
projects, it is recommended that you further organize your
modules into subdirectories inside
lib/. Each such subdirectory becomes a
package.
Importing modules and packages in Stratego is done using the
imports statement. Using imports, you
specify which module from which package to import. See Chapter 11 for an introduction to
modules. There is a direct mapping between the directory name
and the package name, and also between file and module
names. Consider the following main module
lib/ogetarts.str of your library, which
imports all the Stratego modules that constitute the library:
module ogetarts imports ogetarts/main ogetarts/front/parse
The import declaration ogetarts/main states that we
want to import the module main from the package
ogetarts. This tells the Stratego compiler to look
for the file main.str inside the
ogetarts/ directory. The line
ogetarts/front/parse will import the file
parse.str in the
ogetarts/extensions package. On disk, we will have
the following layout:
lib/
ogetarts.str
ogetarts/
main.str
front/
parse.str
In this example, we will assume that the module
ogetarts/main provides a simple evaluator
for arithmetic expressions:
module ogetarts/main imports libstratego-lib Ogetarts strategies ogetarts-eval = bottomup(try(Eval)) rules Eval : Plus(Int(i), Int(j)) -> Int(<addS> (i, j)) Eval : Mul(Int(i), Int(j)) -> Int(<mulS> (i, j))
The module ogetarts/front/parse provides a
strategy for parsing ogetarts expressions:
module ogetarts/front/parse
imports libstratego-sglr libstratego-lib
strategies
parse-ogetarts-stream =
where(tbl := <import-term(Ogetarts.tbl); open-parse-table>)
; finally(
parse-stream(strsglr-report-parse-error | tbl)
, <close-parse-table> tbl
)
So how does the compiler know where to search for the packages
(directories)? This is specified by the -I
option to strc. In our case, we did already
specify lib/ as the basepath for our
library in the section on compiling Stratego programs. Thus, all
module and package references are looked up from there. For
programs using several libraries installed at different
locations, multiple base directories should be specified, each
with the -I option.
In principle, it is possible to import full source of your library
in your Stratego programs. In that case, there is no need to
compile the library separately: it will be
compiled by the Stratego compiler every time the library is
included in a Stratego program. The compiler will act as a
whole-program compiler and compile all the source code from scratch,
including your library sources. This is wasteful, since the
library is recompiled needlessly. To avoid this, the build system
can be told to
compile the library separately to a native library, e.g. a
.so file. The creation
of the native library is done using libtool,
which takes care of creating both static and shared
libraries. On most platforms, the linker prefers shared
libraries over static libraries, given the choice. This means
that linking to your Stratego library will be done dynamically,
unless you or your library user take steps to enable static
linking.
The code below is what goes into your
Makefile.am for you library:
include $(top_srcdir)/Makefile.xt
include $(wildcard *.dep)
lib_LTLIBRARIES = libogetarts.la
pkgdata_DATA = libogetarts.rtree
EXTRA_DIST = $(ogetartssrc) libogetarts.rtree
CLEANFILES = libogetarts.c libogetarts.rtree
libogetarts_la_SOURCES = libogetarts.c
libogetarts_la_LDFLAGS = -avoid-version -no-undefined
libogetarts_la_CPPFLAGS = \
$(STRATEGO_LIB_CFLAGS) $(STRATEGO_RUNTIME_CFLAGS) $(ATERM_CFLAGS)
libogetarts_la_LIBADD = \
$(STRATEGO_SGLR_LIBS) $(STRATEGO_LIB_LIBS) $(STRATEGO_RUNTIME_LIBS) $(ATERM_LIBS)
ogetartssrc = \
ogetarts.str \
$(wildcard $(srcdir)/ogetarts/*.str) \
$(wildcard $(srcdir)/ogetarts/front/*.str)
STRINCLUDES = -I $(top_srcdir)/syn
libogetarts.c libogetarts.rtree : $(ogetartssrc)
@$(STRC)/bin/strc -c --library -i ogetarts.str -o libogetarts.rtree $(STRINCLUDES)
rm libogetarts.str
lib_LTLIBRARIES-
pkgdata_DATA-
libogetarts_LDFLAGS-
libogetarts_CPPLAGS-
libogetarts_LIBADD-
Necessary for some platforms. Note that we add
STRATEGO_SGLR_LIBS, since our module is importinglibstratego-sglr. STRINCLUDES-
For finding the signature and parsetable
libogetarts.c : ...-
Warning: use tab.
If you prefer static over dynamic libraries, you can enforce static
linking by passing the -static option to the
configure of your package via the
LDFLAGS variable:
$ ./configure ... LDFLAGS=-static
Add a program to the tools directory
module ogetarts-eval
imports
libstratego-lib
libogetarts
strategies
io-ogetarts-eval =
io-stream-wrap(
?(<id>, fout)
; parse-ogetarts-stream
; ogetarts-eval
; ?Int(<id>)
; <fputs> (<id>, fout); <fputs> ("\n", fout)
)
Add to tools/Makefile.am:
bin_PROGRAMS = ogetarts-eval ogetarts_eval_LDADD = \ $(top_builddir)/lib/libogetarts.la \ $(STRATEGO_LIB_LIBS) $(STRATEGO_RUNTIME_LIBS) $(ATERM_LIBS)
Invoke the eval tool:
$ echo "1+2" | ./tools/ogetarts-eval
Let's finish up the root build system first, closing with the
ogetarts.spec.in file.
Summary: ogetarts
Name: @PACKAGE_TARNAME@
Version: @PACKAGE_VERSION@
Release: 1
License: LGPL
Group: Development/Tools/Ogetarts
URL: http://www.ogetarts.org/Ogetarts
Source: @PACKAGE_TARNAME@-@PACKAGE_VERSION@.tar.gz
BuildRoot: %{_tmppath}/%{name}-@PACKAGE_VERSION@-buildroot
Requires: aterm >= 2.5
Requires: sdf2-bundle >= 2.4
Requires: strategoxt >= 0.17
Provides: %{name} = %{version}
%description
%prep
%setup -q
%build
CFLAGS="-D__NO_CTYPE" ./configure --prefix=%{_prefix} --with-strategoxt=%{_prefix} \
--with-aterm=%{_prefix} --with-sdf=%{_prefix}
make
%install
rm -rf $RPM_BUILD_ROOT
make DESTDIR=$RPM_BUILD_ROOT install
%clean
rm -rf $RPM_BUILD_ROOT
%files
%defattr(-,root,root,-)
%{_bindir}
%{_libexecdir}
%{_datadir}
%doc
%changelog
This file is not strictly necessary. It's a so-called
.spec-file, which is a package descriptor for
rpm-based distributions. When you provide it, the Stratego/XT build
system can automatically make a .rpm package
file for your project.
In this chapter we learned how to organize Stratego/XT projects, and how to set up the Stratego/XT build system. We saw how the build system, which is based on automake and autoconf, is used to generate many of the artifacts from the syntax definition, such as parse tables and signatures, in the way we discussed in Part II . We also learned how to make stand-alone programs, libraries and XT components from Stratego source code, and how modules and packages relate to files and directories.
More detail can be found by looking at the manual pages for the build tools, such as autoxt, strc, sdf2table, sdf2rtg and xtc. The detailed examples from the Stratego/XT Examples tutorial contain working build systems that can serve as a starting point.
Table of Contents
Even in Stratego/XT, it is not entirely uncommon for developers to produce erroneous code from time to time. This chapter will walk you through the tools and techniques available for hunting down bugs, and tips for how to avoid them in the first place.
Both the Stratego language paradigm and its syntax are rather different from most other languages. Knowing how to use the unique features of Stratego properly, in the way we have described in this manual, goes a long way towards avoiding future maintenance problems.
One important practical aspect of using language constructs is expressing their syntax in a readable manner. The intention behind the code should be apparent for readers of the code. Judicious use of whitespaces is vital in making Stratego code readable, partly because its language constructs are less block-oriented than most Algol-derivates.
The most basic unit of transformation in Stratego is the rewrite rule. The following suggests how rules should be written to maximize readability.
EvalExpr:
Expr(Plus(x), Plus(y) -> Expr(z)
where
<addS> (x,y) => z
Rules are composed using combinators in strategies. One of the
combinators is composition, written
;. It is important to realize that ;
is not a statement terminator, as found in imperative
languages. Therefore, we suggest writing a series of
strategies and rules joined by composition as follows:
eval-all =
EvalExpr
; s1
; s2
Both rules and strategies should be documented, using xDoc. At the
very least, the type of term expected and the type of term returned
should be specified by the @type attribute. Also take
care to specify the arity of lists and tuples, if this is fixed.
/** * @type A -> B */ foo = ...
Inline rules are handy syntactic sugar that should be used with care. Mostly, inline rules are small enough to fit a single line. When they are significantly longer than one line, it is recommended to extract them into a separate, named rule.
strat =
\ x -> y where is-okay(|x) => y \
Formatting concrete syntax depends very much on the language being embedded, so we will provide no hard and fast rules for how to do this.
Formatting of large terms should be done in the style output by pp-aterm.
The Stratego/XT environment does not feature a proper debugger
yet, so the best low-level debugging aids are provided by the
library, in the from of two kinds of strategies, namely
debug and a family based around log.
The debug strategy will print the current term
to stdout. It will not alter
anything. While hunting down a bug in your code, it is
common to sprinkle debug statements liberally
in areas of code which are suspect:
foo =
debug
; bar
; debug
; baz
Sometimes, you need to add additional text to your output, or
do additional formatting. In this case, an idiom with
where and id is used:
foo =
where(<debug> [ "Entered foo : ", <id> ])
; bar
; where(<debug> [ "After bar : ", <id> ])
; baz
The where prevents the current term from being
altered by the construction of your debugging text, and
id is used to retrieve the current term
before the where clause. If, as in this example,
you only need to prepend a string before the current term,
you should rather use debug(s), as shown next.
foo =
debug(!"Entered foo : ")
; bar
; debug(!"After bar : ")
; baz
The use of debug is an effective, but very intrusive
approach. A more disciplined regime has been built on top of
the log(|severity, msg) and
lognl(|severity, msg) strategies.
(See Chapter 25 for details on
log and lognl). The higher-level
strategies you should focus on are fatal-err-msg(|msg),
err-msg(|msg), warn-msg(|msg) and
notice-msg(|msg).
It is recommended that you insert calls to these strategies
at places where your code detects potential and actual
problems. During normal execution of your program, the
output from the various -msg strategies is
silenced. Provided you allow Stratego to deal with the
I/O and command line options, as explained in
Chapter 26, the user (or the
developer doing debugging) can use the
--verbose option to adjust
which messages he wants to be printed as part of
program execution. This way, you get adjustable
levels of tracing output, without having to change
your code by inserting and removing calls to
debug, and without having to recompile.
Some types of errors seem to be more common than others. Awareness of these will help you avoid them in your code.
Strategy and Rule Overloading.
The way Stratego invokes strategies and rules may be a bit
unconventional to some people. We have already seen that
the language allows overloading on name, i.e. you can have
multiple strategies with the same name, and also multiple
rules with the same name. You can even have rules and
strategies which share a common name. When invoking a
name, say s, all rules and strategies with
that name will be considered. During execution the alternatives
are tried in some order, until one succeeds. The language does
not specify the order which the alternatives will be tried.
Eval:
If(t, e1, e2) -> If(t, e1', e2')
where
<simplify> e1 => e1'
; <simplify> e2 => e2'
Eval:
If(False, e1, e2) -> e2
When Eval is called, execution may never
end up in the second case, even though it the current
term is an If term, with the condition
subterm being just the False term.
If you want to control the order in which a set of rules should be tried, you must name each alternative rule differently, and place them behind a strategy that specifies the priority, e.g:
SimplifyIf
If(t, e1, e2) -> If(t, e1', e2')
where
<simplify> e1 => e1'
; <simplify> e2 => e2'
EvalIfCond:
If(False, e1, e2) -> e2
Eval = EvalIfCond <+ SimplifyIf
Combinator Precedence.
The precedence of the composition operator (;) is higher
than that of the choice operators (<+,+,
>+). This means that the expression
s1 < s2 ; s3 should be read as
s1 < (s2 ; s3), and similarly for non-deterministic
choice (+) and right choice (>+). See
Section 15.3 for a more detailed treatment.
Guarded Choice vs if-then-else.
The difference between if s1 then s2 else s3 end and
s1 < s2 + s3 (guarded choice) is whether or not
the result after s1 is passed on to the branches.
For if-then-else, s2 (or
s3) will be applied to the original term, that is,
the effects of s1 are unrolled before proceeding
to the branches. With the guarded choice, this unrolling does
not happen. Refer to Section 15.3.2
for details.
Variable Scoping. Stratego enforces a functional style, with scoped variables. Once a variable has been initialized to a value inside a given scope, it cannot be changed. Variables are immutable. Any attempt at changing the value inside this scope will result in a failure. This is generally a Good Thing, but may at times be the cause of subtle coding errors. Consider the code below:
stratego><map(\ x -> y where !x => y \)> [1] [1]stratego><map(\ x -> y where !x => y \)> [1,1,1,1] [1,1,1,1]stratego><map(\ x -> y where !x => y \)> [1,2,3,4] command failed
Apparently, the map expression works for a singleton
list, a list with all equal elements, but not lists with four different
elements. Why? Let us break this conondrum into pieces and attack
it piece by piece.
First, the inline rule \ x -> y where !x => y \ will
be applied to each element in the list, by map. For
each element, it will bind x to the element, then
build x and assign the result to y.
Thus, for each element in the list, we will assign this element
to y. This explains why it works for lists
with only one element; we never reassign to y. But why
does it work for lists of four equal elements? Because the rule
about immutability is not violated: we do not
change the value of y by
reassigning the same value to it, so Stratego allows us to
do this.
But why does this happen? We clearly stated that we want a local
rule here. The gotcha is that Stratego separates control of scopes
from the local rules. A separate scoping construct,
{y: s} must be used to control the scoping of
variables. If no scoping has been specified, the scope of a
variable will be that of its enclosing named strategy. Thus, the code
above must be written:
stratego> <map({y: \ x -> y where !x => y \})> [1,2,3,4]
[1,2,3,4]
It may be a bit surprising that this works. We have not said anything
about x, so logically, we should not be able to change
this variable either. The difference between x and
y is that x is a pattern variable. Its
lifetime is restricted to the local rule. At first glance, this may
seem a bit arbitrary, but after you code a bit of Stratego, it will
quickly feel natural.
The XT component model is based on Unix pipes. Debugging XT compositions can therefore be done using many of the familiar Unix command line tools.
Checking XTC registrations.
Whenever you call XTC components using xtc-transform,
the location of the component you are calling is looked up in
a component registry. When invoking a component fails, it may
be because the component you are calling has been removed.
Checking the registrations inside a component registry is done
using the xtc command:
# xtc -r /usr/local/apps/dryad/share/dryad/XTC q -a
dryad (0.1pre11840) : /usr/local/apps/dryad/dryad
dryad.m4 (0.1pre11840) : /usr/local/apps/dryad/share/dryad/dryad.m4
...
The -r option is used to specify which registry
you want to inspect. The path given to -r must
be the XTC registry file of your
installed program transformation system that you built with
Stratego/XT. By default, xtc will work
on the Stratego/XT XTC repository, and only list the
components provided by Stratego/XT. This is seldom what
you want.
XTC registries are hierarchical. The XTC repository of your project imports (refers back to) the other projects you used in your build process, such as Stratego/XT itself. The component list you get from xtc when giving it your repository is therefore a full closure of all components visible to transformations in your project.
Now that you know how to obtain the paths for all XT components, it is easy to determine that they actually exist at the locations recorded, and that the access rights are correct.
Programs such as strace may also be useful at the lowest level of debugging, to see which parameters are passed between components, whether a given component is located correctly, and whether execution of a given component succeeds.
Format Checking. Each component in a system built with Stratego/XT accepts a term, definable by some grammar, and outputs another term, also definable by a (possibly the same) grammar. During debugging of XT compositions, it is useful to check that the data flowing between the various components actually conform to the defined grammars. It is not always the case that the grammar in question has been defined, but you are highly encouraged to do so, see Chapter 8 for how to define regular tree grammars.
Once you have a formal declaration of your data, in the form of a regular tree grammar, you can insert calls to the format-check between your XT components to verify data correctness, i.e. the correctness of the terms.
ast2il =
xtc-transform(!"format-check", !["--rtg", "language-ast.rtg"])
; xtc-transform(!"ast2il")
; xtc-transform(!"format-check", !["--rtg", "language-il.rtg"])
The ast2il component transforms from the abstract syntax tree representation of a given language to an intermediate language (IL). format-check is used to verify that the AST passed to ast2il is well-formed, and that the result obtained from ast2il is also well-formed.
Tool Debugging Options.
Most of the XT tools accept a common set of options useful
when debugging. These include --keep, for
adjusting the amount of intermediate results you want to
keep as separate files on disk after transformation,
--verbose for adjusting the level of
debugging information printed by the tool, and
--statistics for displaying runtime
statistics.
The SDF toolkit comes with some very useful debugging aids. The first is the sdfchecker command, which will analyze your SDF definition and offer a list of issues it finds. You do not need to invoke sdfchecker directly. It is invoked by the sdf2table by default, whenever you generate a parse table from a syntax definition. Be advised that the issues pointed to by sdfchecker are not always errors. Nontheless, it is usually prudent to fix them.
The other SDF debugging tool is the visamb command. visamb is used to display ambiguities in parse trees. Its usage is detailed in the command reference (visamb).
Pitfalls with Concrete Syntax.
Doing transformations with concrete syntax in Stratego,
as explained in Chapter 19
depends in the correct placement of .meta
files. When creating, splitting, moving or removing
Stratego source files (.str files), it is
important that you bring along the accompanying
.meta files.
Another thing to be aware of with concrete syntax, is the
presence of reserved meta variables. Typically,
x, xs, e,
t and f have a reserved meaning
inside the concrete syntax fragments as being meta
variables, i.e. variables in the Stratego language, not
in the object language.
A final stumbling block is the general problem of ambiguities in the syntax definition. While SDF allows you to write ambiguous grammars, and sglr accepts these gracefully, you are not allowed to have ambiguous syntax fragments in your Stratego code. In cases where the Stratego compiler (strc) fails due to ambiguous fragments, you can run parse-stratego on your source code to see exactly which parts are ambiguous. The visamb tool should then be applied to the output from parse-stratego to visualize the ambiguities.