Table of Contents
- 3. Architecture
- 4. Annotated Terms
- 5. Syntax Definition and Parsing
- 6. Syntax Definition in SDF
- 7. Advanced Topics in Syntax Definition (*)
- 8. Trees, Terms, and Tree Grammars (*)
- 9. Pretty Printing with GPP (*)
Table of Contents
In this chapter, a general overview is given of the architecture of the XT transformation tools. The technical details of the tools and languages that are involved will be discussed in the follwing chapters.
XT is a collection of components for implementing transformation systems. Some of these components generate code that can be included in a transformation system, such as a parser or pretty-printer. Other components can be used immediately, since they are generic tools. The components of XT are all executable tools: they can be used directly from the command-line.
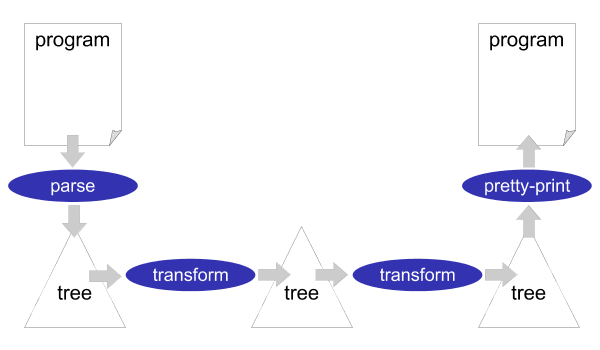
According to the Unix philosophy, the tools that are part of XT all do just one thing (i.e. implement one aspect of a transformation system) and can be composed into a pipeline to combine them in any way you want. A sketch of a typical pipeline is shown in Figure 3.1. First, a parser is applied to a source program. This results in an abstract syntax tree, which is then transformed by a sequence of transformation tools. Finally, the tree is pretty-printed back to a source program. So, this pipeline is a source to source transformation system. The tools that are part of the pipeline exchange structured representations of a program, in the form of an abstract syntax tree. These structured representations can be read in any programming language you want, so the various components of a transformation system can be implemented in different programming languages. Usually, the real transformation components will be implemented in Stratego.
Of course, some compositions are very common. For example, you definitly don't want to enter the complete pipeline of a compiler again and again. So, you want to pre-define such a composition to make it reusable as single tool. For this, you could of create a shell script, but option handling in shell scripts is quite tiresome and you cannot easily add composition specific glue code. To solve this, Stratego itself has a concise library for creating compositions of transformation tools, called XTC. We will come back to that later in Chapter 28.
The nice thing about this approach is that all the tools can be reused in different transformation systems. A parser, pretty-printer, desugarer, optimizer, simplifier, and so an is automatically available to other transformation systems that operate on the same language. Even if a tool will typically be used in a single dominant composition (e.g. a compiler), having the tool available to different transformation systems is very useful. In other words: an XT transformation system is open and its components are reusable.
Programmers write programs as texts using text editors. Some programming environments provide more graphical (visual) interfaces for programmers to specify certain domain-specific ingredients (e.g., user interface components). But ultimately, such environments have a textual interface for specifying the details. So, a program transformation system needs to deal with programs that are in text format.
However, for all but the most trivial transformations, a structured, rather than a textual, representation is needed. Working directly on the textual representation does not give the transformation enough information about what the text actually means. To bridge the gap between the textual and the structured representation, parsers and unparsers are needed. Also, we need to know how this structured representation is actually structured.
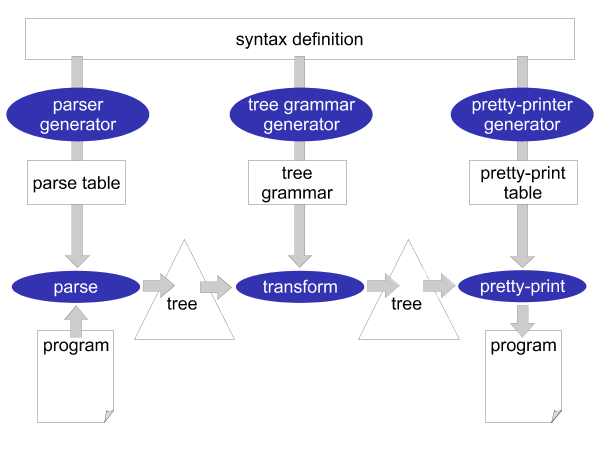
The syntactical rules of a programming language are usually expressed in a context-free grammar. This grammar (or syntax definition) of a programming language plays a central role in Stratego/XT. Most of the XT tools work on a grammar in one way or another. The grammar is a rich source of information. For example, it can be used to generate a parser, pretty-printer, disambiguator, tree grammar, format-checker, and documentation. This central role of a grammar is the most crucial aspect of XT, which is illustrated in Figure 3.2: all the components of a transformation system are directly or indirectly based on the grammar of a programming language.
What makes this all possible is the way syntax is defined in Stratego/XT. Stratego/XT uses the SDF language for syntax definition, which is a very high-level and declarative language for this purpose. SDF does not require the programmer to encode all kinds of properties of a programming language (such as associativity and priorities) in a grammar. Instead, SDF has declarative, concise, ways of defining these properties in such a way that they can actually be understood by tools that take the grammar as an input. And, of course, creating a grammar in such language is much more fun!
As mentioned before, the XT tools exchange a structured representation of a program: an abstract syntax tree. The structure of this abstract syntax tree is called the abstract syntax, as opposed to the ordinary textual syntax, which is called the concrete syntax. In XT, the abstract syntax is directly related to the syntax definition and can be generated from it. The result is a tree grammar that defines the format of the trees that are exchanged between the transformation tools. From the world of XML, you are probably already familiar with tree grammars: DTD, W3C XML Schema and RELAX NG are tree grammars in disguise.
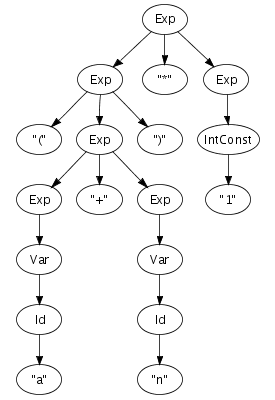
Until now, we have been a bit vague about the format in which abstract syntax trees are actually exchanged between transformation tools. What is this structured program representation?
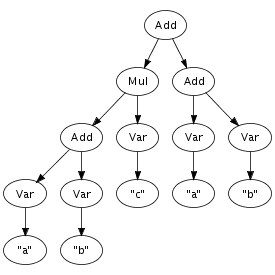
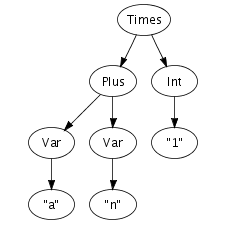
We can easily imagine an abstract syntax tree as a graphical
structure. For example, the tree at the right is a simple
abstract syntax tree for the expression (a + n) *
1. This representation corresponds closely to the
representation of trees in computer memory. However, drawing
pictures is not a very effective way of specifying tree
transformations. We need a concise, textual, way to express an
abstract syntax tree. Fortunately, there is a one-to-one
correspondence between trees and so-called first-order prefix
terms (terms, for short). A term is a constructor, i.e., an
identifier, applied to zero or more terms. Strings and integer
constants are terms as well. Thus, the following term
corresponds to the abstract syntax tree that we have just drawn.
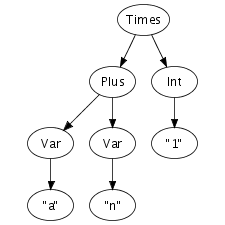
Times(Plus(Var("a"), Var("n")), Int("1"))
In Stratego/XT, programs are exchanged between transformation tools as terms. The exact format we use for terms, is the Annotated Term Format, or ATerms for short. We will discuss this format in more detail later, but some of its features are interesting to note here.
First, ATerms are not only used to exchange programs between tools. ATerms are also used in the Stratego language itself for the representation of programs. In other words, ATerms are used for the external representation as well as the internal representation of programs in Stratego/XT. This is very convenient, since we don't have to bind the ATerms to Stratego specific data-structures. Usually, if such a data-binding is necessary, then there is always a mismatch here and there.
Second, an important feature of the implementation is that terms are represented using maximal sharing. This means that any term in use in a program is represented only once. In other words, two occurrences of the same term will be represented by pointers to the same location. This greatly reduces the amount of memory needed for representing programs.
Table of Contents
The Annotated Term Format, or ATerms for short, is heavily used in Stratego/XT. It used for the structured representation of programs (and also data in general). Program representations are exchanged between transformation tools in the ATerm format and the data-structures of the Stratego language itself are ATerms.
Before we start with the more interesting tools of XT, we need to take a closer look at the ATerm format. This chapter introduces the ATerm format and some tools that operate on ATerms.
The ATerm format provides a set of constructs for representing
trees, comparable to XML or abstract data types in functional
programming languages. For example, the code 4 + f(5 *
x) might be represented in a term as:
Plus(Int("4"), Call("f", [Mul(Int("5"), Var("x"))]))ATerms are constructed from the following elements:
- Integer
-
An integer constant, that is a list of decimal digits, is an ATerm. Examples:
1,12343. - String
-
A string constant, that is a list of characters between double quotes is an ATerm. Special characters such as double quotes and newlines should be escaped using a backslash. The backslash character itself should be escaped as well.
Examples:
"foobar","string with quotes\"","escaped escape character\\ and a newline\n". - Constructor application
-
A constructor is an identifier, that is an alphanumeric string starting with a letter, or a double quoted string.
A constructor application
c(t1,...,tn)creates a term by applying a constructor to a list of zero or more terms. For example, the termPlus(Int("4"),Var("x"))uses the constructorsPlus,Int, andVarto create a nested term from the strings"4"and"x".When a constructor application has no subterms the parentheses may be omitted. Thus, the term
Zerois equivalent toZero(). Some people consider it good style to explicitly write the parentheses for nullary terms in Stratego programs. Through this rule, it is clear that a string is really a special case of a constructor application. - List
-
A list is a term of the form
[t1,...,tn], that is a list of zero or more terms between square brackets.While all applications of a specific constructor typically have the same number of subterms, lists can have a variable number of subterms. The elements of a list are typically of the same type, while the subterms of a constructor application can vary in type.
Example: The second argument of the call to
"f"in the termCall("f",[Int("5"),Var("x")])is a list of expressions. - Tuple
-
A tuple
(t1,...,tn)is a constructor application without constructor. Example:(Var("x"), Type("int")) - Annotation
-
The elements defined above are used to create the structural part of terms. Optionally, a term can be annotated with a list terms. These annotations typically carry additional semantic information about the term. An annotated term has the form
t{t1,...,tn}. Example:Lt(Var("n"),Int("1")){Type("bool")}. The contents of annotations is up to the application.
As a Stratego programmer you will be looking a lot at raw ATerms. Stratego pioneers would do this by opening an ATerm file in emacs and trying to get a sense of the structure by parenthesis highlighting and inserting newlines here and there. These days your life is much more pleasant through the tool pp-aterm, which adds layout to a term to make it readable. For example, parsing the following program
let function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n - 1))
in printint(fact(10))
end
produces the following ATerm (say in file fac.trm):
Let([FunDecs([FunDec("fact",[FArg("n",Tp(Tid("int")))],Tp(Tid("int")),
If(Lt(Var("n"),Int("1")),Int("1"),Seq([Times(Var("n"),Call(Var("fact"),
[Minus(Var("n"),Int("1"))]))])))])],[Call(Var("printint"),[Call(Var(
"fact"),[Int("10")])])])
By pretty-printing the term using pp-aterm as
$ pp-aterm -i fac.trm
we get a much more readable term:
Let(
[ FunDecs(
[ FunDec(
"fact"
, [FArg("n", Tp(Tid("int")))]
, Tp(Tid("int"))
, If(
Lt(Var("n"), Int("1"))
, Int("1")
, Seq(
[ Times(
Var("n")
, Call(
Var("fact")
, [Minus(Var("n"), Int("1"))]
)
)
]
)
)
)
]
)
]
, [ Call(
Var("printint")
, [Call(Var("fact"), [Int("10")])]
)
]
)
An important feature of the implementation is that terms are represented using maximal sharing. This means that any term in use in a program is represented only once. In other words, two occurrences of the same term will be represented by pointers to the same location. Figure 4.1 illustrates the difference between a pure tree representation and a tree, or more accurately, a directed acyclic graph, with maximal sharing. That is, any sub-term is represented exactly once in memory, with each occurrence pointing to the same memory location. This representation entails that term equality is a constant operation, since it consists of comparing pointers.
It should be noted that annotations create different terms, that is, two terms, one with and the other without annotations that are otherwise, modulo annotations, the same, are not equal.
Maximal sharing can make a big difference in the amount of bytes needed for representing programs. Therefore, we would like to preserve this maximal sharing when an ATerm is exchanged between two programs. When exporting a term using the textual exchange format, this compression is lost. Therefore, the ATerm Library also provides a binary exchange format that preserves maximal sharing.
Actually, there are three different formats:
- Textual ATerm Format
-
In the textual ATerm format the ATerm is written as plain text, without sharing. This format is very inefficient for the exchange of large programs, but it is readable for humans.
- Binary ATerm Format
-
The binary ATerm format, also known as BAF, is an extremely efficient binary encoding of an ATerm. It preserves maximal sharing and uses all kinds of tricks to represent an ATerm in as few bytes as possible.
- Shared Textual ATerm Format
-
In the shared, textual, format the ATerm is written as plain text, but maximal sharing is encoded in the text.
The tool baffle can be used to convert an ATerm from one format to another. Baffle, and other tools that operate on ATerms, automatically detect the format of an input ATerm.
The ATerm Format is an external representation for terms that can be used to exchange structured data between programs. In order to use a term, a program needs to parse ATerms and transform them into some internal representation. To export a term after processing it, a program should transform the internal representation into the standard format. There are libraries supporting these operation for a number of languages, including C, Java, and Haskell.
The implementation of the Stratego transformation language is based on the C implementation of the library. The library provides term input and output, and an API for constructing and inspecting terms. Garbage collection is based on Boehms conservative garbage collection algorithm.
Table of Contents
In Chapter 3 we have introduced the architecture of the XT tansformation tools. Source to source transformation systems based on XT consist of a pipeline of a parser, a series of transformations on a structured program representation, and a pretty-printer. In Chapter 4 we have explained the ATerm format, which is the format we use for this structured program transformation. This chapter will be about the parser part of the pipeline.
Stratego/XT uses the Syntax Definition Formalism (SDF), for defining the syntax of a programming language. From a syntax definition in SDF, a parser can be generated fully automatically. There is no need for a separate lexer or scanner specification, since SDF integrates the lexical and the context-free syntax definition of a programming language in a single specification. The generated parser is based on the Scannerless Generalized-LR algorithm, but more details about that later. The parser directly produces an ATerm representation of the program, as a parse tree, or as an abstract syntax tree.
Actually, the component-based approach of XT allows you to use any tool for parsing a source program to an ATerm. So, you don't necessarily have to use the parsing tools we present in this chapter. Instead, it might sometimes be a good idea to create an ATerm backend for a parser that you already have developed (by hand or using a different parser generator), or reuse an entire, existing front-end that is provided by a third-party. However, the techniques we present in this chapter are extremely expressive, flexible, and easy to use, so for developing a new parser it would be a very good idea to use SDF and SGLR.
In this section, we review the basics of grammars, parse trees and abstract syntax trees. Although you might already be familiar with these basic concepts, the perspective from the Stratego/XT point of view might still be interesting to read.
Context-free grammars were originally introduced by Chomsky to describe the generation of grammatically correct sentences in a language. A context-free grammar is a set of productions of the form A0 -> A1 ... An, where A0 is non-terminal and A1 ... An is a string of terminals and non-terminals. From this point of view, a grammar describes a language by generating its sentences. A string is generated by starting with the start non-terminal and repeatedly replacing non-terminal symbols according to the productions until a string of terminal symbols is reached.
A context-free grammar can also be used to recognize sentences in the language. In that process, a string of terminal symbols is rewritten to the start non-terminal, by repeatedly applying grammar productions backwards, i.e. reducing a substring matching the right-hand side of a production to the non-terminal on the left-hand side. To emphasize the recognition aspect of grammars, productions are specified as A1 ... An -> A0 in SDF.
As an example, consider the SDF productions for a small language
of arithmetic expressions in Figure 5.1, where Id
and IntConst are terminals and Var and
Exp are non-terminals. Using this definition, and
provided that a and n are identifiers
(Id) and 1 is an
IntConst, a string such as (a+n)*1 can
be recognized as an expression by reducing it to
Exp, as shown by the reduction sequence in the
right-hand side of Figure 5.1.
Figure 5.1. Context-free productions and a reduction sequence.
Id -> Var
Var -> Exp
IntConst -> Exp
"-" Exp -> Exp
Exp "*" Exp -> Exp
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
"(" Exp ")" -> Exp
|
(a + n ) * 1 -> (Id + n ) * 1 -> (Var + n ) * 1 -> (Exp + n ) * 1 -> (Exp + Id ) * 1 -> (Exp + Var) * 1 -> (Exp + Exp) * 1 -> (Exp ) * 1 -> Exp * 1 -> Exp * IntConst -> Exp * Exp -> Exp |
Recognition of a string only leads to its grammatical category, not to any other information. However, a context-free grammar not only describes a mapping from strings to sorts, but actually assigns structure to strings. A context-free grammar can be considered as a declaration of a set of trees of one level deep. For example, the following trees correspond to productions from the syntax definition in Figure 5.1:
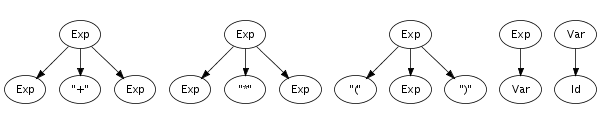
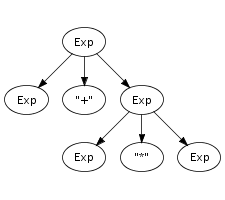
Such one-level trees can be composed into larger trees by fusing
trees such that the symbol at a leaf of one tree matches with
the root symbol of another, as is illustrated in the fusion of
the plus and times productions on the right.
The fusion process can continue as long as the tree has
non-terminal leaves. A tree composed in this fashion is a parse
tree if all leaves are terminal symbols. Figure 5.2 shows a parse tree for the expression
(a+n)*1, for which we showed a reduction sequence
earlier in Figure 5.1. This
illustrates the direct correspondence between a string and its
grammatical structure. The string underlying a parse tree can be
obtained by concatening the symbols at its leaves, also known as
the yield.
Parse trees can be derived from the reduction sequence induced by the productions of a grammar. Each rewrite step is associated with a production, and thus with a tree fragment. Instead of replacing a symbol with the non-terminal symbol of the production, it is replaced with the tree fragment for the production fused with the trees representing the symbols being reduced. Thus, each node of a parse tree corresponds to a rewrite step in the reduction of its underlying string. This is illustrated by comparing the reduction sequence in Figure 5.1 with the tree in Figure 5.2
The recognition of strings described by a syntax definition, and the corresponding construction of parse trees can be done automatically by a parser, which can be generated from the productions of a syntax definition.
Parse trees contain all the details of a program including
literals, whitespace, and comments. This is usually not
necessary for performing transformations. A parse tree is
reduced to an abstract syntax tree by
eliminating irrelevant information such as literal symbols and
layout. Furthermore, instead of using sort names as node labels,
constructors encode the production from
which a node is derived. For this purpose, the productions in a
syntax definition are extended with constructor
annotations. Figure 5.3 shows
the extension of the syntax definition from Figure 5.1 with constructor
annotations and the abstract syntax tree for the same good old
string (a+n)*1. Note that some identifiers are used
as sort names and and as constructors. This
does not lead to a conflict since sort names and constructors
are derived from separate name spaces. Some productions do not
have a constructor annotation, which means that these
productions do not create a node in the abstract syntax tree.
Figure 5.3. Context-free productions with constructor annotations and an abstract syntax tree.
Id -> Var {cons("Var")}
Var -> Exp
IntConst -> Exp {cons("Int")}
"-" Exp -> Exp {cons("Uminus")}
Exp "*" Exp -> Exp {cons("Times")}
Exp "+" Exp -> Exp {cons("Plus")}
Exp "-" Exp -> Exp {cons("Minus")}
Exp "=" Exp -> Exp {cons("Eq")}
Exp ">" Exp -> Exp {cons("Gt")}
"(" Exp ")" -> Exp
|  |
In the next section we will take a closer look at the various features of the SDF language, but before that it is useful to know your tools, so that you can immediately experiment with the various SDF features you will learn about. You don't need to fully understand the SDF fragments we use to explain the tools: we will come back to that later.
One of the nice things about SDF and the tools for it, is that the concepts that we have discussed directly translate to practice. For example, SDF supports all context-free grammars; the parser produces complete parse trees, which can even be yielded; parse trees can be converted to abstract syntax trees.
In SDF, you can split a syntax definition into multiple
modules. So, a complete syntax definition consists of a set
modules. SDF modules are stored in files with the extension
.sdf. Figure 5.4 shows
two SDF modules for a small language of expressions. The module
Lexical defines the identifiers and integer
literals of the language. This module is imported by the module
Expression.
Figure 5.4. SDF modules for a small language of arithmetic expressions.
module Expression
imports
Lexical Operators
exports
context-free start-symbols Exp
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")}
"(" Exp ")" -> Exp {bracket}
|
module Operators
exports
sorts Exp
context-free syntax
Exp "*" Exp -> Exp {left, cons("Times")}
Exp "/" Exp -> Exp {left, cons("Div")}
Exp "%" Exp -> Exp {left, cons("Mod")}
Exp "+" Exp -> Exp {left, cons("Plus")}
Exp "-" Exp -> Exp {left, cons("Minus")}
context-free priorities
{left:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
|
module Lexical
exports
sorts Id IntConst
lexical syntax
[\ \t\n] -> LAYOUT
[a-zA-Z]+ -> Id
[0-9]+ -> IntConst
|
Before you can invoke the parser generator to create a parser
for this expression language, the modules that constitute a
complete syntax definition have to be collected into a single
file, usually called a definition. This
file has the extension .def. Collecting SDF
modules into a .def file is the job of the
tool pack-sdf.
$ pack-sdf -i Expression.sdf -o Expression.def
Pack-sdf collects all modules imported by the SDF module
specified using the -i parameter. This results in a
combined syntax definition, which is written to the file
specified with the -o parameter. Modules are looked
for in the current directory and any of the include directories
indicated with the -I dir arguments.
Pack-sdf does not analyse the contents of an SDF module to report possible errors (except for syntactical ones). The parser generator, discussed next, performs this analysis.
Standard options for input and output
All tools in Stratego/XT use the -i and
-o options for input and output. Also, most tools
read from the standard input or write to standard output if no
input or output is specified.
From the .def definition file (as produced by
pack-sdf), the parser
generator sdf2table constructs
a parse table. This parse table can later on be handed off to
the actual parser.
$ sdf2table -i Expression.def -o Expression.tbl -m Expression
The -m option is used to specify the module for
which to generate a parse table. The default module is
Main, so if the syntax definition has a different
main module (in this case Expression), then you
need to specify this option.
The parse table is stored in a file with extension
.tbl. If all you plan on doing with your grammar is
parsing, the resulting .tbl file is all you need to
deploy. sdf2table could be thought of as a
parse-generator; however, unlike many other parsing systems, it
does not construct an parser program, but a compact data
representation of the parse table.
Sdf2table analyzes the SDF syntax definition to detect possible
errors, such as undefined symbols, symbols for which no
productions exists, deprecated features, etc. It is a good idea
to try to fix these problems, although sdf2table
will usually still happily generated a parse table for you.
Now we have a parse table, we can invoke the actual parser with
this parse table to parse a source program. The parser is called
sglr and produces a
complete parse tree in the so-called AsFix
format. Usually, we are not really interested in the parse tree
and want to work on an abstract syntax tree. For this, there is
the somewhat easier to use tool sglri,
which indirectly just invokes sglr.
$cat mul.exp (a + n) * 1$sglri -p Expression.tbl -i mul.exp Times(Plus(Var("a"),Var("n")),Int("1"))
For small experiments, it is useful that sglri can also read the source file from standard input. Example:
$ echo "(a + n) * 1" | sglri -p Expression.tbl
Times(Plus(Var("a"),Var("n")),Int("1"))
Heuristic Filters. As we will discuss later, SGLR uses disambiguation filters to select the desired derivations if there are multiple possibilities. Most of these filters are based on specifications in the original syntax definition, such a associativity, priorities, follow restrictions, reject, avoid and prefer productions. However, unfortunately there are some filters that select based on heuristics. Sometimes these heuristics are applicable to your situation, but sometimes they are not. Also, the heuristic filters make it less clear when and why there are ambiguities in a syntax definition. For this reason, they are disabled by default if you use sglri, (but not yet if you use sglr).
Start Symbols.
If the original syntax definition contained multiple start
symbols, then you can optionally specify the desired start
symbol with the -s option. For example, if we add
Id to the start-symbols of our
expression language, then a single identifier is suddenly an
ambiguous input (we will come back to ambiguities later) :
$ echo "a" | sglri -p Expression.tbl
amb([Var("a"),"a"])
By specifying a start symbol, we can instruct the parser to give us the expression alternative, which is the first term in the list of two alternatives.
$ echo "a" | sglri -p Expression.tbl -s Exp
Var("a")Working with Parse Trees. If you need a parse tree, then you can use sglr itself. These parse trees contain a lot of information, so they are huge. Usually, you really don't want to see them. Still, the structure of the parse tree is quite interesting, since you can exactly inspect how the productions from the syntax definition have been applied to the input.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | pp-aterm
parsetree( ... )
Note that we passed the options -2 -fi -fe to
sglr. The -2 option specifies the
variant of the AsFix parse tree format that should be used:
AsFix2. The Stratego/XT tools use this variant at the
moment. All variants of the AsFix format are complete and
faithful representation of the derivation constructed by the
parser. It includes all details of the input file, including
whitespace, comments, and is self documenting as it uses the
complete productions of the syntax definition to encode node
labels. The AsFix2 variant preserves all the structure of the
derivation. In the other variant, the structure of the lexical
parts of a parse tree are not preserved. The -fi
-fe options are used to heuristic disambiguation filters,
which are by default disabled in sglri, but not in
sglr.
The parse tree can be imploded to an abstract syntax tree
using the tool implode-asfix. The
combination of sglr and
implode-asfix has the same effect as directly
invoking sglri.
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | implode-asfix
Times(Plus(Var("a"),Var("n")),Int("1"))The parse tree can also be yielded back to the original source file using the tool asfix-yield. Applying this tool shows that whitespace and comments are indeed present in the parse tree, since the source is reproduced in exactly the same way as it was!
$ echo "(a + n) * 1" | sglr -p Expression.tbl -2 -fi -fe | asfix-yield
(a + n) * 1Table of Contents
First, basic structure of SDF. Second, how syntax is defined SDF. Third, examples of lexical and context-free syntax. Fourth, more detailed coverage of disambigation.
In this section, we give an overview of the basic constructs of SDF. After this section, you will now the basic idea of SDF. The next sections will discuss these constructs more detail.
Before defining some actual syntax, we have to explain the basic structure of a module. For this, let's take a closer look at the language constructs that are used in the modules we showed earlier in Figure 5.4.
Example 6.1. Basic constructs of SDF
module Expressionimports Lexical Operators
exports
context-free start-symbol Exp
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")} "(" Exp ")" -> Exp {bracket} module Operators exports sorts Exp
context-free syntax Exp "*" Exp -> Exp {left, cons("Times")}
Exp "/" Exp -> Exp {left, cons("Div")} Exp "%" Exp -> Exp {left, cons("Mod")} Exp "+" Exp -> Exp {left, cons("Plus")} Exp "-" Exp -> Exp {left, cons("Minus")} context-free priorities
{left: Exp "*" Exp -> Exp Exp "/" Exp -> Exp Exp "%" Exp -> Exp } > {left: Exp "+" Exp -> Exp Exp "-" Exp -> Exp } module Lexical exports sorts Id IntConst
lexical syntax
[a-zA-Z]+ -> Id [0-9]+ -> IntConst [\ \t\n] -> LAYOUT lexical restrictions
Id -/- [a-zA-Z]
Example 6.1 shows these modules, highlighting some of the constructs that are important to know before we dive into the details of defining syntax.
Usually, parsing is performed in two phases. First, a lexical analysis phase splits the input in tokens, based on a grammar for the lexical syntax of the language. This lexical grammar is usually specified by a set of regular expressions that specifiy the tokens of the language. Second, a parser based on a grammar for the context-free syntax of the language performs the syntactic analysis. This approach has several disadvantages for certain applications, which won't discuss in detail for now. One of the most important disadvantages is that the combination of the two grammars is not a complete, declarative definition of the syntax of the language.
SDF integrates the definition of lexical and context-free syntax
in a single formalism, thus supporting the
complete description of the syntax of a
language in a single specification. All syntax, both lexical and
context-free, is defined by productions,
respectively in lexical syntax and
context-free syntax sections. Parsing of languages
defined in SDF is implemented by scannerless generalized-LR
parsing, which operates on individual characters instead of
tokens.
Expressive Power. Since lexical and context-free syntax are both defined by productions, there is actually no difference in the expressive power of the lexical and context-free grammar. Hence, lexical syntax can be a context-free language, instead of being restricted to a regular grammar, which is the case when using conventional lexical analysis tools based on regular expression. For example, this means that you can define the syntax of nested comments in SDF, which we will illustrate later. In practice, more important is that it is easier to define lexical syntax using productions than using regular expressions.
Layout. Then, why are there two different sections for defining syntax? The difference between these two kinds of syntax sections is that in lexical syntax no layout (typically whitespace and comments) is allowed between symbols. In contrast, in context-free syntax sections layout is allowed between the symbols of a production. We will explain later how layout is defined. The allowance of layout is the only difference between the two kinds of syntax sections.
In the Section 5.1 we recapped context-free grammars and productions, which have the form A0 -> A1 ... An, where A0 is non-terminal and A1 ... An is a string of terminals and non-terminals. Also, we mentioned earlier that the distinction between terminals and non-terminals is less useful in SDF, since only single characters are terminals if the lexical and context-free syntax are defined in a single formalism. For this reason, every element of a production, i.e. A0 ... An is called a symbol. So, productions take a list of symbols and produce another symbol.
There are two primary symbols:
- Sorts
-
Sorts are names for language specific constructs, such as
Exp,Id, andIntConst. These names are declared using the previously introducedsortsdeclaration and defined by productions. - Character Classes
-
A character class is set of characters. Character classes are specified by single characters, character ranges, and can be combined using set operators, such as complement, difference, union, intersection. Examples:
[abc],[a-z],[a-zA-Z0-9],~[\n]. We will discuss character classes in more detail in Section 6.2.4.
Of course, defining an entire language using productions that
can contain only sorts and character classes would be a lot of
work. For example, programming languages usually contain all
kinds of list constructs. Specification of lists with plain
context-free grammars requires several productions for each list
construct. SDF provides a bunch of regular expression operators
abbreviating these common patterns. In the following list,
A represents a symbol and c a
character.
-
"c0 ... cn" -
Literals are strings that must literally occur in the input, such as keywords (
if,while,class), literals (null,true) and operators (+,*). Literals can be written naturally as, for example,"while". Escaping of special characters will be discussed in ???. A*-
Zero or more symbols
A. Examples:Stm*,[a-zA-Z]* A+-
One or more symbols
A. Examples:TypeDec+,[a-zA-Z]+ {A0 A1}*-
Zero or more symbols
A0separated byA1. Examples:{Exp ","}*,{FormalParam ","}* {A0 A1}+-
One or more symbols
A0separated byA1. Examples:{Id "."}+,{InterfaceType ","}+ A?-
Optional symbol
A. Examples:Expr?,[fFdD]? A0 | A1-
Alternative of symbol
A0orA1. Example:{Expr ","}* | LocalVarDec (A0 ... An)-
Sequence of symbols
A0 ... An.
In order to define the syntax at the level of characters, SDF
provides character classes, which represent a set of characters
from which one character can be recognized during parsing. The
content of a character classes is a specification of single
characters or character ranges
(c0-c1). Letters
and digits can be written as themselves, all other characters
should be escaped using a slash,
e.g. \_. Characters can also be indicated by their
decimal ASCII code, e.g. \13 for linefeed. Some
often used non-printable characters have more mnemonic names,
e.g., \n for newline, \ for space and
\t for tab.
Character classes can be combined using set operations. The most
common one is the unary complement operator ~, e.g
~[\n]. Binary operators are the set difference
/, union \/ and intersection
/\.
Example 6.2. Examples of Character Classes
-
[0-9] -
Character class for digits: 0, 1, 2, 3, 4, 5, 6, 8, 9.
-
[0-9a-fA-F] -
Characters typically used in hexi-decimal literals.
-
[fFdD] -
Characters used as a floating point type suffix, typically in C-like languages.
-
[\ \t\12\r\n] -
Typical character class for defining whitespace. Note that SDF does not yet support \f as an escape for form feed (ASCII code 12).
-
[btnfr\"\'\\] -
Character class for the set of characters that are usually allowed as escape sequences in C-like programming languages.
-
~[\"\\\n\r] -
The set of characters that is typically allowed in string literals.
Until now, we have mostly discussed the design of SDF. Now, it's about time to see how all these fancy ideas for syntax definition work out in practice. In this and the next section, we will present a series of examples that explain how typical language constructs are defined in SDF. This first section covers examples of lexical syntax constructs. The next section will be about context-free syntax.
Before we can start with the examples of lexical constructs like
identifiers and literals, you need to know the basics of
defining whitespace. In SDF, layout is a special sort, called
LAYOUT. To define layout, you have to define
productions that produce this LAYOUT sort. Thus, to
allow whitespace we can define a production that takes all
whitespace characters and produces layout. Layout is lexical
syntax, so we define this in a lexical syntax section.
lexical syntax [\ \t\r\n] -> LAYOUT
We can now also reveal how context-free syntax
exactly works. In context-free syntax, layout is
allowed between symbols in the left-hand side of the
productions, by automatically inserting optional layout
(e.g. LAYOUT?) between them.
In the following examples, we will assume that whitespace is always defined in this way. So, we will not repeat this production in the examples. We will come back to the details of whitespace and comments later.
Almost every language has identifiers, so we will start with that. Defining identifiers themselves is easy, but there is some more definition of syntax required, as we will see next. First, the actual definition of identifiers. As in most languages, we want to disallow digits as the first character of an identifier, so we take a little bit more restrictive character class for that first character.
lexical syntax [A-Za-z][A-Za-z0-9]* -> Id
If a language would only consists of identifiers, then this
production does the job. Unfortunately, life is not that easy.
In practice, identifiers interact with other language
constructs. The best known interaction is that most languages
do not allow keywords (such as if,
while, class) and special literals
(such as null, true). In SDF,
keywords and special literals are not automatically preferred
over identifiers. For example, consider the following, very
simple expression language (for the context-free syntax we
appeal to your intuition for now).
lexical syntax
[A-Za-z][A-Za-z0-9]* -> Id
"true" -> Bool
"false" -> Bool
context-free start-symbols Exp
context-free syntax
Id -> Exp {cons("Id")}
Bool -> Exp {cons("Bool")}
The input true can now be parsed as an identifier
as well as a boolean literal. Since the generalized-LR parser
actually supports ambiguities, we can even try this out:
$ echo "true" | sglri -p Test.tbl
amb([Bool("true"), Id("true")])
The amb term is a representation of the
ambiguity. The argument of the ambiguity is a list of
alternatives. In this case, the first is the boolean literal
and the second is the identifier true. So, we have to define
explicitly that we do not want to allow these boolean literals
as identifiers. For this purpose, we can use SDF
reject productions. The intuition of
reject productions is that all
derivations of a symbol for which there is a reject production
are forbidden. In this example, we need to create productions
for the boolean literals to identifiers.
lexical syntax
"true" -> Id {reject}
"false" -> Id {reject}
For true, there will now be two derivations for
an Id: one using the reject production and one
using the real production for identifiers. Because of that
reject production, all derivations will be rejected, so
true is not an identifier anymore. Indeed, if we
add these productions to our syntax definition, then the true
literal is no longer ambiguous:
$ echo "true" | sglri -p Test.tbl
Bool("true")
We can make the definition of these reject productions a bit
more concise by just reusing the Bool sort. In
the same way, we can define keywords using separate production
rules and have a single reject production from keywords to
identifiers.
lexical syntax
Bool -> Id {reject}
Keyword -> Id {reject}
"class" -> Keyword
"if" -> Keyword
"while" -> Keyword
Scanners usually apply a longest match policy for scanning tokens. Thus, if the next character can be included in the current token, then this will always be done, regardless of the consequences after this token. In most languages, this is indeed the required behaviour, but in some languages longest match scanning actually doesn't work. Similar to not automatically reserving keywords, SDF doesn't choose the longest match by default. Instead, you need to specify explicitly that you want to recognize the longest match.
For example, suppose that we introduce two language constructs
based on the previously defined Id. The following
productions define two statements: a simple goto and a
construct for variable declarations, where the first
Id is the type and the second the variable name.
context-free syntax
Id -> Stm {cons("Goto")}
Id Id -> Stm {cons("VarDec")}
For the input foo, which is of course intended to
be a goto, the parser will now happily split up the identifier
foo, which results in variable
declarations. Hence, this input is ambiguous.
$ echo "foo" | sglri -p Test.tbl
amb([Goto("foo"), VarDec("f","oo"), VarDec("fo","o")])
To specify that we want the longest match of an identifier, we
define a follow restriction. Such a
follow restriction indicates that a string of a certain symbol
cannot be followed by a character from the given character
class. In this way, follow restrictions can be used to encode
longest match disambiguation. In this case, we need to specify
that an Id cannot be followed by one of the
identifier characters:
lexical restrictions Id -/- [A-Za-z0-9]
Indeed, the input foo is no longer ambiguous and
is parsed as a goto:
$ echo "foo" | sglri -p Test.tbl
Goto("foo")
In Section 6.3.2 we
explained how to reject keywords as identifiers, so we will not
repeat that here. Also, we discussed how to avoid that
identifiers get split. A similar split issue arises with
keywords. Usually, we want to forbid a letter immediately after
a keyword, but the scannerless parser will happily start a new
identifier token immediately after the keyword. To illustrate
this, we need to introduce a keyword, so let's make our previous
goto statement a bit more clear:
context-free syntax
"goto" Id -> Stm {cons("Goto")}
To illustrate the problem, let's take the input
gotox. Of course, we don't want to allow this
string to be a goto, but without a follow restriction, it will
actually be parsed by starting an identifier after the
goto:
$ echo "gotox" | sglri -p Test.tbl
Goto("x")
The solution is to specify a follow restriction on the
"goto" literal symbol.
lexical restrictions "goto" -/- [A-Za-z0-9]
It is not possible to define the follow restrictions on the
Keyword sort that we introduced earlier in the
reject example. The follow restriction must be
defined on the symbol that literally occurs
in the production, which is not the case with the
Keyword symbol. However, you can specify all the
symbols in a single follow restriction, seperated by spaces:
lexical restrictions "goto" "if" -/- [A-Za-z0-9]
Compared to identifiers, integer literals are usually very easy to define, since they do not really interact with other language constructs. Just to be sure, we still define a lexical restriction. The need for this restriction depends on the language in which the integer literal is used.
lexical syntax [0-9]+ -> IntConst lexical restrictions IntConst -/- [0-9]
In mainstream languages, there are often several notations for
integer literal, for example decimal, hexadecimal, or octal. The
alternatives are then usually prefixed with one or more
character that indicates the kind of integer literal. In Java,
hexadecimal numerals start with 0x and octal with a
0 (zero). For this, we have to make the definition
of decimal numerals a bit more precise, since 01234
is now an octal numeral.
lexical syntax "0" -> DecimalNumeral [1-9][0-9]* -> DecimalNumeral [0][xX] [0-9a-fA-F]+ -> HexaDecimalNumeral [0] [0-7]+ -> OctalNumeral
Until now, the productions for lexical syntax have not been very complex. In some cases, the definition of lexical syntax might even seem to be more complex in SDF, since you explicitly have to define behaviour that is implicit in existing lexical anlalysis tools. Fortunately, the expressiveness of lexical syntax in SDF also has important advantages, even if it is applied to language that are designed to be processed with a separate scanner. As a first example, let's take a look at the definition of floating-point literals.
Floating-point literals consists of three elements: digits,
which may include a dot, an exponent, and a float suffix
(e.g. f, d etc). There are three
optional elements in float literals: the dot, the exponent, and
the float suffix. But, if you leave them all out, then the
floating-point literal no longer distinguishes itself from an
integer literal. So, one of the floating-point specific elements
is required. For example, valid floating-point literals are:
1.0, 1., .1,
1f, and 1e5, but invalid are:
1, and .e5. These rules are encoded in
the usual definition of floating-point literals by duplicating
the production rule and making different elements optional and
required in each production. For example:
lexical syntax [0-9]+ "." [0-9]* ExponentPart? [fFdD]? -> FloatLiteral [0-9]* "." [0-9]+ ExponentPart? [fFdD]? -> FloatLiteral [0-9]+ ExponentPart [fFdD]? -> FloatLiteral [0-9]+ ExponentPart? [fFdD] -> FloatLiteral [eE] SignedInteger -> ExponentPart [\+\-]? [0-9]+ -> SignedInteger
However, in SDF we can use reject
production to reject these special cases. So, the
definition of floating-point literals itself can be more
naturally defined in a single production  . The reject production
. The reject production  defines that there
should at least be one element of a floating-point literal: it
rejects plain integer literals. The reject production
defines that there
should at least be one element of a floating-point literal: it
rejects plain integer literals. The reject production  defines that the digits part of the
floating-point literals is not allowed to be a single dot.
defines that the digits part of the
floating-point literals is not allowed to be a single dot.
lexical syntax FloatDigits ExponentPart? [fFdD]? -> FloatLiteral[0-9]* "." [0-9]* -> FloatDigits [0-9]+ -> FloatDigits [0-9]+ -> FloatLiteral {reject}
"." -> FloatDigits {reject}
Similar to defining whitespace, comments can be allowed
everywhere by defining additional LAYOUT
productions. In this section, we give examples of how to define
several kinds of common comments.
Most languages support end-of-line comments, which start with
special characters, such as //, #,
or %. After that, all characters on that line are
part of the comment. Defining end-of-line comments is quite
easy: after the initial characters, every character except for
the line-terminating characters is allowed until a line
terminator.
lexical syntax "//" ~[\n]* [\n] -> LAYOUT
Block comments (i.e. /* ... */) are a bit more
tricky to define, since the content of a block comment may
include an asterisk (*). Let's first take a look
at a definition of block comments that does not allow an
asterisk in its content:
"/*" ~[\*]* "*/" -> LAYOUT
If we allow an asterisk and a slash, the sequence
*/ will be allowed as well. So, the parser will
accept the string /* */ */ as a comment, which is
not valid in C-like languages. In general, allowing this in a
language would be very inefficient, since the parser can never
decide where to stop a block comment. So, we need to disallow
just the specific sequence of characters */
inside a comment. We can specify this using a follow
restriction: an asterisk in a block comments is
allowed, but it cannot be followed by a slash
(/).
But, on what symbol do we specify this follow restriction? As
explained earlier, we need to specify this follow restriction
on a symbol that literally occurs in the
production. So, we could try to allow a "*", and
introduce a follow restriction on that:
lexical syntax "/*" (~[\*] | "*")* "*/" -> LAYOUT lexical restrictions "*" -/- [\/]
But, the symbol "*" also occurs in other
productions, for example in multiplication expressions and we
do not explicitly say here that we intend to refer to the
"*" in the block comment production. To
distinguish the block comment asterisk from the multiplication
operator, we introduce a new sort, creatively named
Asterisk, for which we can specify a follow
restriction that only applies to the asterisk in a block
comment.
lexical syntax "/*" (~[\*] | Asterisk)* "*/" -> LAYOUT [\*] -> Asterisk lexical restrictions Asterisk -/- [\/]
To illustrate that lexical syntax in SDF can actually be
context-free, we now show an example of how to implement
balanced, nested block comments, i.e. a block comment that
supports block comments in its content: /* /* */
*/. Defining the syntax for nested block comments is
quite easy, since we can just define a production that allows
a block comment inside itself  . For performance and
predictability, it is important to require that the comments
are balanced correctly. So, in addition to disallowing
. For performance and
predictability, it is important to require that the comments
are balanced correctly. So, in addition to disallowing
*/ inside in block comments, we now also have to
disallow /*. For this, we introduce a
Slash sort, for which we define a follow
restriction 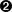 ,
similar to the
,
similar to the Asterisk sort that we discussed in
the previous section.
lexical syntax BlockComment -> LAYOUT "/*" CommentPart* "*/" -> BlockComment ~[\/\*] -> CommentPart Asterisk -> CommentPart Slash -> CommentPart BlockComment -> CommentPart[\/] -> Slash [\*] -> Asterisk lexical restrictions Asterisk -/- [\/] Slash -/- [\*]
Context-free syntax in SDF is syntax where layout is allowed between the symbols of the productions. Context-free syntax can be defined in a natural way, thanks to the use of generalized-LR parsing, declarative disambiguation mechanism, and an extensive set of regular expression operators. To illustrate the definition of context-free syntax, we give examples of defining expressions and statements. Most of the time will be spend on explaining the disambiguation mechanisms.
In the following sections, we will explain the details of a slightly extended version of the SDF modules in Example 6.1, shown in Example 6.3.
Example 6.3. Syntax of Small Expression Language in SDF
module Expression
imports
Lexical
exports
context-free start-symbols Exp
context-free syntax
Id -> Var 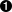 Var -> Exp {cons("Var")
Var -> Exp {cons("Var") 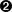 }
IntConst -> Exp {cons("Int")
}
IntConst -> Exp {cons("Int")  }}
"(" Exp ")" -> Exp {bracket
}}
"(" Exp ")" -> Exp {bracket  }
"-" Exp -> Exp {cons("UnaryMinus")}
Exp "*" Exp -> Exp {cons("Times"), left
}
"-" Exp -> Exp {cons("UnaryMinus")}
Exp "*" Exp -> Exp {cons("Times"), left  }
Exp "/" Exp -> Exp {cons("Div"), left}
Exp "%" Exp -> Exp {cons("Mod"), left}
Exp "+" Exp -> Exp {cons("Plus")
}
Exp "/" Exp -> Exp {cons("Div"), left}
Exp "%" Exp -> Exp {cons("Mod"), left}
Exp "+" Exp -> Exp {cons("Plus")  , left}
Exp "-" Exp -> Exp {cons("Minus"), left}
Exp "=" Exp -> Exp {cons("Eq"), non-assoc
, left}
Exp "-" Exp -> Exp {cons("Minus"), left}
Exp "=" Exp -> Exp {cons("Eq"), non-assoc  }
Exp ">" Exp -> Exp {cons("Gt"), non-assoc}
context-free priorities
}
Exp ">" Exp -> Exp {cons("Gt"), non-assoc}
context-free priorities  "-" Exp -> Exp
"-" Exp -> Exp  > {left:
> {left:  Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
> {non-assoc:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
> {non-assoc:  Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
}
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp
}
First, it is about time to explain the constructor attribute,
cons, which was already briefly mentioned in Section 5.1.2. In the example
expression language, most productions have a constructor
attribute, for example 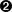 ,
,  and
and  ,
but some have not, for example
,
but some have not, for example  and
and  .
.
The cons attribute does not have any actual meaning
in the definition of the syntax, i.e the presence or absence of
a constructor does not affect the syntax that is defined in any
way. The constructor only serves to specify the name of the
abstract syntax tree node that is to be constructed if that
production is applied. In this way, the cons
attribute  of the production for
integer literals, defines that an
of the production for
integer literals, defines that an Int node should
be produced for that production:
$ echo "1" | sglri -p Test.tbl
Int("1")
Note that this Int constructor takes a single
argument, a string, which is the name of the variable. This
argument of Int is a string because the production
for IntConst is defined in lexical
syntax and all derivations from lexical syntax
productions are represented as strings, i.e. without
structure. As another example, the production for addition has a
Plus constructor attribute  . This production has three symbols on
the left-hand side, but the constructor takes only two
arguments, since literals are not included in the abstract
syntax tree.
. This production has three symbols on
the left-hand side, but the constructor takes only two
arguments, since literals are not included in the abstract
syntax tree.
$ echo "1+2" | sglri -p Test.tbl
Plus(Int("1"),Int("2"))
However, there are also productions that have no
cons attribute, i.e.  and
and  . The production
. The production  from
from Id to
Var is called an injection,
since it does not involve any additional syntax. Injections
don't need to have a constructor attribute. If it is left out,
then the application of the production will not produce a node
in the abstract syntax tree. Example:
$ echo "x" | sglri -p Test.tbl
Var("x")
Nevertheless, the production  does involve additional syntax, but does not have a
constructor. In this case, the
does involve additional syntax, but does not have a
constructor. In this case, the bracket attribute
should be used to indicate that this is a symbol between
brackets, which should be literals. The bracket
attribute does not affect the syntax of the language, similar to
the constructor attribute. Hence, the parenthesis in the
following example do not introduce a node, and the
Plus is a direct subterm of Times.
$ echo "(1 + 2) * 3" | sglri -p Test.tbl
Times(Plus(Int("1"),Int("2")),Int("3"))Conventions. In Stratego/XT, constructors are by covention CamelCase. Constructors may be overloaded, i.e. the same name can be used for several productions, but be careful with this feature: it might be more difficult to distinguish the several cases for some tools. Usually, constructors are not overloaded for productions with same number of arguments (arity).
Example 6.4. Ambiguous Syntax Definition for Expressions
Exp "+" Exp -> Exp {cons("Plus")}
Exp "-" Exp -> Exp {cons("Minus")}
Exp "*" Exp -> Exp {cons("Mul")}
Exp "/" Exp -> Exp {cons("Div")}
Syntax definitions that use only a single non-terminal for
expressions are highly ambiguous. Example 6.4 shows the basic arithmetic
operators defined in this way. For every combination of
operators, there are now multiple possible derivations. For
example, the string a+b*c has two possible
derivations, which we can actually see because of the use of a
generalized-LR parser:
$ echo "a + b * c" | sglri -p Test3.tbl | pp-aterm
amb(
[ Times(Plus(Var("a"), Var("b")), Var("c"))
, Plus(Var("a"), Times(Var("b"), Var("c")))
]
)
These ambiguities can be solved by using the associativities and
priorities of the various operators to disallow undesirable
derivations. For example, from the derivations of a + b *
c we usually want to disallow the second one, where the
multiplications binds weaker than the addition operator. In
plain context-free grammars the associativity and priority rules
of a language can be encoded in the syntax definition by
introducing separate non-terminals for all the priority levels
and let every argument of productions refer to such a specific
priority level. Example 6.5
shows how the usual priorities and associativity of the
operators of the example can be encoded in this way. For
example, this definition will never allow an AddExp
as an argument of a MulExp, which implies that
* binds stronger than +. Also,
AddExp can only occur at the left-hand side of an
AddExp, which makes the operator left associative.
This way of dealing with associativity and priorities has several disadvantages. First, the disambiguation is not natural, since it is difficult to derive the more high-level rules of priorities and associativity from this definition. Second, it is difficult to define expressions in a modular way, since the levels need to be known and new operators might affect the carefully crafted productions for the existing ones. Third, due to all the priority levels and the productions that connect these levels, the parse trees are more complex and parsing is less efficient. For these reasons SDF features a more declarative way of defining associativity and priorities, which we discuss in the next section.
Example 6.5. Non-Ambiguous Syntax Definition for Expressions
AddExp -> Exp
MulExp -> AddExp
AddExp "+" MulExp -> AddExp {cons("Plus")}
AddExp "-" MulExp -> AddExp {cons("Minus")}
PrimExp -> MulExp
MulExp "*" PrimExp -> MulExp {cons("Mul")}
MulExp "/" PrimExp -> MulExp {cons("Div")}
IntConst -> PrimExp {cons("Int")}
Id -> PrimExp {cons("Var")}
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
In order to support natural syntax definitions, SDF provides
several declarative disambiguation mechanisms. Associativity
declarations (left, right,
non-assoc), disambiguate combinations of a binary
operator with itself and with other operators. Thus, the left
associativity of + entails that a+b+c
is parsed as (a+b)+c. Priority declarations
(>) declare the relative priority of productions. A
production with lower priority cannot be a direct subtree of a
production with higher priority. Thus a+b*c is
parsed as a+(b*c) since the other parse
(a+b)*c has a conflict between the *
and + productions.
... > Exp "&" Exp -> Exp > Exp "^" Exp -> Exp > Exp "|" Exp -> Exp > Exp "&&" Exp -> Exp > Exp "||" Exp -> Exp > ...
This is usually handled with introducing a new non-terminal.
context-free syntax
"new" ArrayBaseType DimExp+ Dim* -> ArrayCreationExp {cons("NewArray")}
Exp "[" Exp "]" -> Exp {cons("ArrayAccess")}
ArrayCreationExp "[" Exp "]" -> Exp {reject}
Figure 6.1 illustrates the use of
these operators in the extension of the expression language with
statements and function declarations. Lists are used in numerous
places, such as for the sequential composition of statements
(Seq), the declarations in a let binding, and the
formal and actual arguments of a function (FunDec
and Call). An example function definition in this
language is:
Figure 6.1. Syntax definition with regular expressions.
module Statements
imports Expressions
exports
sorts Dec FunDec
context-free syntax
Var ":=" Exp -> Exp {cons("Assign")}
"(" {Exp ";"}* ")" -> Exp {cons("Seq")}
"if" Exp "then" Exp "else" Exp -> Exp {cons("If")}
"while" Exp "do" Exp -> Exp {cons("While")}
"let" Dec* "in" {Exp ";"}* "end" -> Exp {cons("Let")}
"var" Id ":=" Exp -> Dec {cons("VarDec")}
FunDec+ -> Dec {cons("FunDecs")}
"function" Id "(" {Id ","}* ")"
"=" Exp -> FunDec {cons("FunDec")}
Var "(" {Exp ","}* ")" -> Exp {cons("Call")}
context-free priorities
{non-assoc:
Exp "=" Exp -> Exp
Exp ">" Exp -> Exp}
> Var ":=" Exp -> Exp
> {right:
"if" Exp "then" Exp "else" Exp -> Exp
"while" Exp "do" Exp -> Exp}
> {Exp ";"}+ ";" {Exp ";"}+ -> {Exp ";"}+
context-free start-symbols Exp
function fact(n, x) = if n > 0 then fact(n - 1, n * x) else x
Parse-unit is a tool, part of Stratego/XT, for testing SDF syntax definitions. The spirit of unit testing is implemented in parse-unit by allowing you to check that small code fragments are parsed correctly with your syntax definition.
In a parse testsuite you can define tests with an input and an
expected result. You can specify that a test should succeed
(succeeds, for lazy people), fail
(fails) or that the abstract syntax tree should have
a specific format. The input can be an inline string or the
contents of a file for larger tests.
Assuming the following grammar for a simple arithmetic expressions:
module Exp
exports
context-free start-symbols Exp
sorts Id IntConst Exp
lexical syntax
[\ \t\n] -> LAYOUT
[a-zA-Z]+ -> Id
[0-9]+ -> IntConst
context-free syntax
Id -> Exp {cons("Var")}
IntConst -> Exp {cons("Int")}
Exp "*" Exp -> Exp {left, cons("Mul")}
Exp "/" Exp -> Exp {left, cons("Div")}
Exp "%" Exp -> Exp {left, cons("Mod")}
Exp "+" Exp -> Exp {left, cons("Plus")}
Exp "-" Exp -> Exp {left, cons("Minus")}
context-free priorities
{left:
Exp "*" Exp -> Exp
Exp "/" Exp -> Exp
Exp "%" Exp -> Exp
}
> {left:
Exp "+" Exp -> Exp
Exp "-" Exp -> Exp
}
You could define the following parse testsuite in a file
expression.testsuite :
testsuite Expressions
topsort Exp
test simple int literal
"5" -> Int("5")
test simple addition
"2 + 3" -> Plus(Int("2"), Int("3"))
test addition is left associative
"1 + 2 + 3" -> Plus(Plus(Int("1"), Int("2")), Int("3"))
test
"1 + 2 + 3" succeeds
test multiplication has higher priority than addition
"1 + 2 * 3" -> Plus(Int("1"), Mul(Int("2"), Int("3")))
test
"x" -> Var("x")
test
"x1" -> Var("x1")
test
"x1" fails
test
"1 * 2 * 3" -> Mul(Int("1"), Mul(Int("2"), Int("3")))
Running this parse testsuite with:
$ parse-unit -i expression.testsuite -p Exp.tbl
will output:
-----------------------------------------------------------------------
executing testsuite Expressions with 9 tests
-----------------------------------------------------------------------
* OK : test 1 (simple int literal)
* OK : test 2 (simple addition)
* OK : test 3 (addition is left associative)
* OK : test 4 (1 + 2 + 3)
* OK : test 5 (multiplication has higher priority than addition)
* OK : test 6 (x)
sglr: error in g_0.tmp, line 1, col 2: character `1' (\x31) unexpected
* ERROR: test 7 (x1)
- parsing failed
- expected: Var("x1")
sglr: error in h_0.tmp, line 1, col 2: character `1' (\x31) unexpected
* OK : test 8 (x1)
* ERROR: test 9 (1 * 2 * 3)
- succeeded: Mul(Mul(Int("1"),Int("2")),Int("3"))
- expected: Mul(Int("1"),Mul(Int("2"),Int("3")))
-----------------------------------------------------------------------
results testsuite Expressions
successes : 7
failures : 2
-----------------------------------------------------------------------
You cannot escape special characters because there is no need to escape them. The idea of the testsuite syntax is that test input typically contains a lot of special characters, which therefore they should no be special and should not need escaping.
Anyhow, you still need some mechanism make it clear where the
test input stops. Therefore the testsuite syntax supports
several quotation symbols. Currently you can choose from:
", "", """, and
[, [[, [[[. Typically, if
you need a double quote in your test input, then you use the
[.
Parse-unit has an option to parse a single test and write the
result to the output. In this mode ambiguities are accepted,
which is useful for debugging. The option for the 'single test
mode' is --single
where nrnr is the number in the
testsuite (printed when the testsuite is executed). The
--asfix2 flag can be used to produce an asfix2
parse tree instead of an abstract syntax tree.
The following make rule can be used to invoke parse-unit from your build system.
%.runtestsuite : %.testsuite
$(SDF_TOOLS)/bin/parse-unit -i $< -p $(PARSE_UNIT_PTABLE) --verbose 1 -o /dev/null
A typical Makefile.am fo testing your
syntax definitions looks like:
EXTRA_DIST = $(wildcard *.testsuite)
TESTSUITES = \
expressions.testsuite \
identifiers.testsuite
PARSE_UNIT_PTABLE = $(top_srcdir)/syn/Foo.tbl
installcheck-local: $(TESTSUITES:.testsuite=.runtestsuite)
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
Import module and rename symbols in the imported definition.
Not very common, but heavily used for combining syntax definitions of different language. See concrete object syntax.
Modules can have formal parameters.
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
Format-check analyzes whether the input ATerm conforms to the format that is specified in the RTG (Regular Tree Grammar).
Format-check verifies that the input ATerm is part of the language defined in the RTG. If this is not the case, then the ATerm contains format errors. Format-check can operate in three modes: plain, visualize and XHTML.
The plain mode is used if the other modes are not enabled. In the plain mode format errors are reported and no result is written the the output (stdout or a file). Hence, if format-check is included in a pipeline, then the following tool will probably fail. If the input term is correct, then it is written to the output.
The visualize mode is enabled with the --vis
option. In visualize mode format errors are reported and in a
pretty-printed ATerm will be written to the output. All
innermost parts of the ATerm that cause format errors are
printed in red, if your terminal supports control characters
for colors. If you want to browse through the ATerm with less,
then you should use the -r flag.
The XHTML mode is enabled with the --xhtml
option. In XHTML mode format errors are reported and an report
in XHTML will be written to the output. This report shows the
parts of the ATerm that are not formatted correctly. Also,
moving with your mouse over the nodes of ATerm, will show the
non-terminals that have be inferred by format-check (do not use
IE6. Firefox or Mozilla is recommended).
Format-check reports all innermost format errors. That is, only the deepest format errors are reported. A format error is reported by showing the ATerm that is not in the correct format, and the inferred types of the children of the ATerm. In XHTML and visualize mode a format error of term in a list is presented by a red comma and term. This means that a type has been inferred for the term itself, but that it is not expected at this point in the list. If only the term is red, then no type could be inferred for the term itself.
In all modes format-check succeeds (exit code 0) if the ATerm contains no format errors. If the term does contain format errors, then format-check fails (exit code 1).
Consider the RTG generated in the example of sdf2rtg:
regular tree grammar
start Exp
productions
Exp -> Minus(Exp,Exp)
Exp -> Plus(Exp,Exp)
Exp -> Mod(Exp,Exp)
Exp -> Div(Exp,Exp)
Exp -> Mul(Exp,Exp)
Exp -> Int(IntConst)
Exp -> Var(Id)
IntConst -> <string>
Id -> <string>
The ATerm
Plus(Var("a"), Var("b"))
is part of the language defined by this RTG. Therefore, format-check succeeds:
$ format-check --rtg Exp.rtg -i exp1.trm
Plus(Var("a"),Var("b"))
$
Note that format-check outputs the input term in this case. In this way format-check can be used in a pipeline of tools. On the other hand, the ATerm
Plus(Var("a"), Var(1))
is not part of the language defined by this RTG. Therefore, the invocation of format-check fails. Format-check also reports which term caused the failure:
$ format-check --rtg Exp.rtg -i exp2.trm
error: cannot type Var(1)
inferred types of subterms:
typed 1 as <int>
$
In large ATerms it might be difficult to find the incorrect
subterm. To help with this, format-check supports the
--vis argument. If this argument is used, then the
result will pretty-printed (in the same way as pp-aterm) and the incorrect parts
will be printed in red.
For example, consider this term:
Plus(Mul(Int(1), Var("a")), Minus(Var("b"), Div(1, Var("c"))))
format-check will visualize the errors in this ATerm:

The XHTML mode shows the errors in red as well. Moreover, if you move your moves over the terms, then you'll see the inferred types of the term.
$ format-check --rtg Exp.rtg -i exp3.trm --xhtml -o foo.html
You can now view the resulting file in your browser. You need a decent browser (Firefox or Mozilla. no IE).
The abstract syntax of a programming language or data format can
be described by means of an algebraic
signature. A signature declares for each constructor
its arity m, the sorts of its arguments S1 *
... * Sm, and the sort of the resulting term
S0 by means of a constructor declaration c:S1 *
... * Sm -> S0. A term can be validated against a
signature by a format checker.
Signatures can be derived automatically from syntax definitions.
For each production A1...An -> A0 {cons(c)} in a
syntax definition, the corresponding constructor declaration is
c:S1 * ... * Sm -> S0, where the Si are
the sorts corresponding to the symbols Aj after
leaving out literals and layout sorts. Figure 8.1 shows the signatures of statement and
expression constructors for the example language from this
chapter. The modules have been derived automatically from the
syntax definitions in ??? and
Figure 6.1.
Figure 8.1. Signature for statement and expression constructors, automatically derived from a syntax definition.
module Statements
signature
constructors
FunDec : Id * List(Id) * Exp -> FunDec
FunDecs : List(FunDec) -> Dec
VarDec : Id * Exp -> Dec
Call : Var * List(Exp) -> Exp
Let : List(Dec) * List(Exp) -> Exp
While : Exp * Exp -> Exp
If : Exp * Exp * Exp -> Exp
Seq : List(Exp) -> Exp
Assign : Var * Exp -> Exp
Gt : Exp * Exp -> Exp
Eq : Exp * Exp -> Exp
Minus : Exp * Exp -> Exp
Plus : Exp * Exp -> Exp
Times : Exp * Exp -> Exp
Uminus : Exp -> Exp
Int : IntConst -> Exp
: Var -> Exp
Var : Id -> Var
: String -> IntConst
: String -> Id
signature
constructors
Some : a -> Option(a)
None : Option(a)
signature
constructors
Cons : a * List(a) -> List(a)
Nil : List(a)
Conc : List(a) * List(a) -> List(a)
sdf2rtg -i m.def -o m.rtg -m M
.
sdf2rtg derives from an SDF syntax definition
m.def a regular tree grammar for the module
M and all modules it imports.
rtg2sig -i m.def -o m.rtg
.
rtg2sig generates from a regular tree grammar a
Stratego signature.
Table of Contents
Work in Progress
This chapter is work in progress. Not all parts have been finished yet. The latest revision of this manual may contain more material. Refer to the online version.
The GPP package is a tool suite for generic pretty-printing. GPP supports pretty-printing of parse-trees in the AsFix format with comment preservation and of abstract syntax trees. GPP supports the output formats plain text, LaTeX, and HTML. Formattings are defined in pretty print tables, which can be generated from SDF syntax definitions.
The Box language is used in the GPP framework as a language-independent intermediate representation. The input language dependent parts and the output format dependent parts of GPP are connected through this intermediate representation.
Box is a mark-up language to describe the intended layout of text
and is used in pretty print
tables. A Box expression is constructed by composing
sub-boxes using Box operators. These operators specify the
relative ordering of boxes. Examples of Box operators are the
H and V operator which
format boxes horizontally and vertically, respectively.
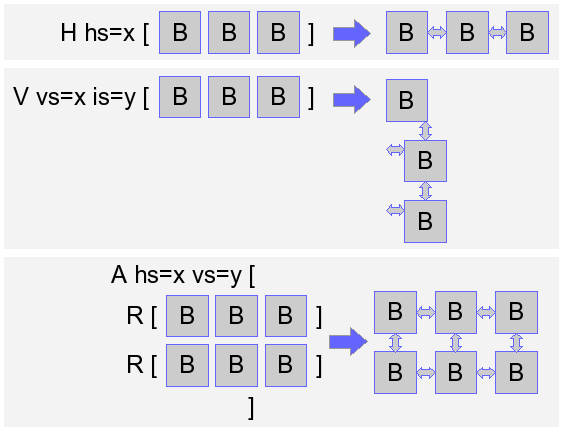
The exact formatting of each Box operator can be customized using
Box options. For example, to control the horizontal layout between
boxes the H operator supports the
hs space option.
For a detailed description of Box (including a description of all available Box operators) we refer to To Reuse Or To Be Reused (Chapter 4)
Pretty-print tables are used to specify how language constructs have to be pretty-printed. Pretty-print tables are used in combination with GPP front-ends, such ast2abox.
Pretty-print tables use Box as language to specify formatting of language constructs. A pretty-print table contains mappings from constructor names to Box expressions. For example, for the SDF production
Exp "+" Exp -> Exp {cons("Plus")}
A pretty-print entry looks like:
Plus -- H hs=1 [ _1 "+" _2]
Pretty-print tables are ordered such that pretty-print rules occuring first take preceedence over overlapping pretty-print rules defined later. The syntax of pretty-print tables is available in GPP.
Pretty-print tables can be generated from SDF syntax definitions using ppgen. Generated pretty-print rules can easiliy be customized by overruling them in additional pretty-print tables. The tool pptable-diff notifies inconsistensies in pretty-print tables after the syntax definition has changed and can be used to bring inconsistent table up-to-date.
To be able to specify formattings for all nested constructs that are allowed in SDF productions, so called selectors are used in pretty-print tables to refer to specific parts of an SDF production and to define a formatting for them. For example, the SDF prodcution
"return" Exp? ";" -> Stm {cons("Return")}
contains a nested symbol A?. To specify a formatting for this production, two pretty-print entries can be used:
Return -- H [ KW["return"] _1 ";" ] Return.1:opt -- H [ _1 ]
A selector consists of a constructor name followed by a list of number+type tuples. A number selects a particular subtree of a constructor application, the type denotes the type of the selected construct (sequence, optional, separated list etc.). This rather verbose selector mechanism allows unambiguous selection of subtrees. Its verbosity (by specifying both the number of a subtree and its type), makes pretty-print tables easier to understand and, more importantly, it enables pretty-printing of AST's, because with type information, a concrete term can be correctly recontructed from an AST. Pretty-print tables can thus be used for both formatting of parse-trees and AST's.
Below we summarize which selector types are available:
- opt
-
For SDF optionals
S? - iter
-
For non-empty SDF lists
S+ - iter-star
-
For possible empty SDF lists
S* - iter-sep
-
For SDF separator lists
{S1 S2}+. Observe that the symbolS1and the separatorS2are ordinary subtrees of the iter-sep construct which can be refered to as first and second subtree, respectively. - iter-star-sep
-
For SDF separator lists
{S1 S2}*. Its symbolS1and separatorS2can be refered to as first and second sub tree. - alt
-
For SDF alternatives
S1 | S2 | S3. According to the SDF syntax, alternatives are binary operators. The pretty-printer flattens all subsequent alternatives. Pretty-print rules can be specified for each alternative individually by specifying the number of each alternative. To be able to format literals in alternative, a special formatting rule can be defined for the construct (See the examples below). - seq
-
For SDF alternatives
(S1 S2 S3).
Below we list a simple SDF module with productions containing all above rule selectors.
module Symbols
exports
context-free syntax
A? -> S {cons("ex1")}
A+ -> S {cons("ex2")}
A* -> S {cons("ex3")}
{S1 S2}+ -> S {cons("ex4")}
{S1 S2}* -> S {cons("ex5")}
"one" | "two" | S? -> S {cons("ex6")}
("one" "two" S? ) -> S {cons("ex7")}
The following pretty-print table shows which pretty-print rules can be defined for this syntax:
[ ex1 -- _1, ex1.1:opt -- _1, ex2 -- _1, ex2.1:iter -- _1, ex3 -- _1, ex3.1:iter-star -- _1, ex4 -- _1, ex4.1:iter-sep -- _1 _2, ex5 -- _1, ex5.1:iter-star-sep -- _1 _2, ex6 -- _1, ex6.1:alt -- KW["one"] KW["two"] _1, ex6.1:alt.1:opt -- _1, ex7 -- _1, ex7.1:seq -- KW["one"] KW["two"] _1, ex7.1:seq.1:opt -- _1 ]
The pretty-print rule ex6.1:alt is a special
case. It contains three Box expressions, one for each
alternative. It is used to specify a formatting for the
non-nested literals "one" and
"two". During pretty-printing one of the three Box
expressions is selected, depending on alternative contained the
term to format.
In this section, we explain how you can generate a tool that restores all parentheses at the places where necessary according to the priorities and associativities of a language.
In this section, we explain how you can use Box in Stratego to implement a pretty-printer by hand.
After transformation, an abstract syntax tree should be turned into text again to be useful as a program. Mapping a tree into text can be seen as the inverse as parsing, and is thus called unparsing. When an unparser makes an attempt at producing human readable, instead of just compiler parsable, program text, an unparser is called a pretty-printer. We use the pretty-printing model as provided by the Generic Pretty-Printing package GPP. In this model a tree is unparsed to a Box expression, which contains text with markup for pretty-printing. A Box expression can be interpreted by different back-ends to produce text for different displaying devices, such as plain ASCII text, HTML, and LaTeX.
Unparsing is the inverse of parsing composed with abstract syntax tree composition. That is, an unparser turns an abstract syntax tree into a string, such that if the resulting string is parsed again, it produces the same abstract syntax tree.
An unparser can be organized in two phases. In the first phase,
each node in an abstract syntax tree is replaced with the concrete
syntax tree of the corresponding grammar production. In the
second phase, the strings at the leaves of the tree are
concatenated into a string. Figure 9.1
illustrates this process. The replacement of abstract syntax tree
nodes by concrete syntax patterns should be done according to the
productions of the syntax definition. An unparsing table is an
abstraction of a syntax definition definining the inverse mapping
from constructors to concrete syntax patterns. An entry c --
s1 ... sn defines a mapping for constructor c
to the sequence s1 ... sn, where each
s_i is either a literal string or a parameter
_i referring to the ith argument of the
constructor. Figure 9.2 shows an
unparsing table for some expression and statement
constructors. Applying an unparsing mapping to an abstract syntax
tree results in a tree structure with strings at the leafs, as
illustrated in Figure 9.1.
Figure 9.2. Unparsing table
[
Var -- _1,
Int -- _1,
Plus -- _1 "+" _2,
Minus -- _1 "-" _2,
Assign -- _1 ":=" _2,
Seq -- "(" _1 ")",
Seq.1:iter-star-sep -- _1 ";",
If -- "if" _1 "then" _2 "else" _3,
Call -- _1 "(" _2 ")",
Call.2:iter-star-sep -- _1 ","
]
Although the unparse of an abstract syntax tree is a text that can be parsed by a compiler, it is not necessarily a readable text. A pretty-printer is an unparser attempting to produce readable program text. A pretty-printer can be obtained by annotating the entries in an unparsing table with markup instructing a typesetting process. Figure 9.3 illustrates this process.
Box is a target independent formatting language, providing
combinators for declaring the two-dimensional positioning of boxes
of text. Typical combinators are H[b_1...b_n], which
combines the b_i boxes horizontally, and
V[b_1...b_n], which combines the
b_i boxes vertically. Figure 9.4 shows a pretty-print table with
Box markup. A more complete overview of the Box language and the
GPP tools can be found in Chapter 9.
Figure 9.4. Pretty-print table with Box markup
[
Var -- _1,
Int -- _1,
Plus -- H[_1 "+" _2],
Minus -- H[_1 "-" _2],
Assign -- H[_1 ":=" _2],
Seq -- H hs=0["(" V[_1] ")"],
Seq.1:iter-star-sep -- H hs=0[_1 ";"],
If -- V[V is=2[H["if" _1 "then"] _2]
V is=2["else" _3]],
Call -- H hs=0[_1 "(" H[_2] ")"],
Call.2:iter-star-sep -- H hs=0[_1 ","]
]
Figure 9.5. Pretty-printing of if-then-else statement
If(Eq(Var("n"),Int("1")),
Int("0"),
Times(Var("n"),
Call(Var("fac"),[Minus(Var("n"),Int("1"))])))


if n = 1 then 0 else n * fac(n - 1)
Note: correct pretty-printing of an abstract syntax tree requires
that it contains nodes representing parentheses in the right
places. Otherwise, reparsing a pretty-printed string might get a
different interpretation. The sdf2parenthesize
tool generates from an SDF definition a Stratego program that
places parentheses at the necessary places in the tree.
ppgen -i m.def -o m.pp
.
Ppgen generates from an SDF syntax definition a
pretty-print table with an entry for each context-free syntax
production with a constructor annotation. Typically it is
necessary to edit the pretty-print table to add appropriate Box
markup to the entries. The result should be saved under a
different name to avoid overwriting it.
ast2abox -p m.pp -i file.ast -o file.abox
.
ast2abox maps an abstract syntax tree
file.ast to an abstract syntax representation
file.abox of a Box term based on a pretty-print
table m.pp.
abox2text -i file.abox -o file.txt
.
abox2text formats a Box term as ASCII text.
pp-aterm -i file1.trm -o file2.trm
.
pp-aterm formats an ATerm as an ATerm in text
format, adding newlines and indentation to make the structure of
the term understandable. This is a useful tool to inspect terms
while debugging transformations.
term-to-dot -i file.trm -o file.dot (--tree | --graph)
.
Term-to-dot is another visualization tool for terms
that creates a dot graph representation, which can
be visualized using the dot tool from the graphviz
graph layout package. Term-to-dot can produce an
expanded tree view (--tree), or a directed acyclic
graph view (--graph) preserving the maximal sharing
in the term. This tool was used to produce the tree
visualizations in this chapter.
This tool is not part of the Stratego/XT distribution, but
included in the Stratego/XT Utilities package.